5 支持向量机

5 支持向量机

本章介绍了现代机器学习中理论上最活跃、实践上最有效的分类算法之一：支持向量机（SVM）。首先介绍了可分离数据集的算法，然后给出了其对不可分数据集的通用版本，最后基于边缘概念为支持向量机提供了理论基础。我们首先描述线性分类问题。

5.1线性分类

考虑一个输入空间 $x$ ，它是 $\mathbb R^N$ 的子集其中 $N \ge 1$ ，且输出或目标空间 $y =\{−1，+1\}$，设 $f:x\to y$ 是目标函数。给定一个假设集 $\mathcal H$ 的函数映射 $x$ 到 $y$，二元分类任务的公式如下。学习者从 $X$ 处根据未知分布 $\mathcal D$ ， $S =((x_1,y_1),...,(x_m,y_m))\in (x\times y)^m$，对于所有 $i\in [m]$， $y_i=f(x_i)$ ，获得一个大小为 $m$ 的训练样本 $S$ 绘制i.i.d.。问题在于确定一个假设 $h\in\mathcal H$ 、 二元分类器，小的泛化误差：

$$R_{\mathcal D}(h)=\underset {x\sim\mathcal D}{\mathbb P}[h(x)\neq f(x)].(5.1)$$

可以为此任务选择不同的假设集 $\mathcal H$ 。第三章将奥卡姆的剃刀原理形式化，从第三章的结果来看，复杂度较小的假设集——例如，较小的VC维度或Rademacher复杂度——在其他条件相同的情况下，提供更好的学习保证。复杂度相对较小的自然假设集是线性分类器或超平面的假设集，其定义如下：

$$\mathcal H =\{x\mapsto sign(\bf w\cdot x+\Bbb b ):w\in\mathbb R^N,\Bbb b\in\mathbb R\}.(5,2)$$

然后将学习问题称为线性分类问题。 $\mathbb R^N$ 中超平面的一般方程为 $\bf w\cdot x+\Bbb b=0$ ，其中 $\bf w\in \mathbb R^N$ 是一个垂直于超平面的非零向量， $b \in R$ 是一个标量.

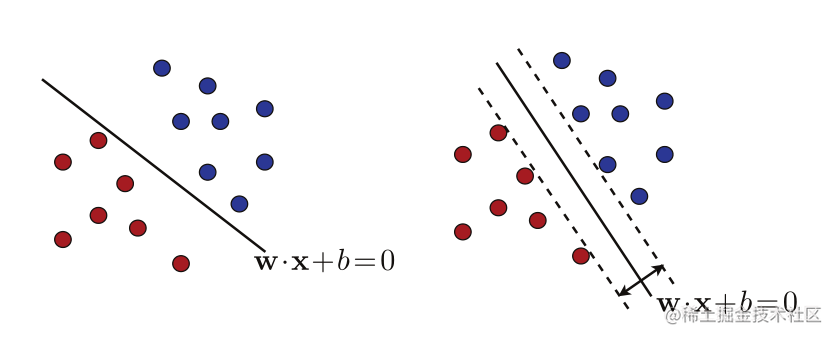
图5.1

两个可能的分离超平面。右边的图显示了一个使边距最大化的超平面。

5.2可分离情况

在本节中，我们假设训练样本 $S$ 可以线性分离，也就是说，我们假设存在一个超平面，该超平面将训练样本完美地分离为两个正标记点和负标记点的总体，如图5.1的左面板所示。这相当于 $(\bf w,\Bbb b)\in(\mathbb R^N-\{0\})\times \mathbb R$ 的存在使得

$$\forall i\in[m],y_i(\bf w\cdot x_i+\Bbb b)\ge 0.(5.3)$$

但是，如图5.1所示，这样的分离超平面是无限多的。学习算法应该选择哪个超平面？支持向量机解的定义基于几何余量的概念。

定义5.1（几何边界）

几何边界 $p_h(\bf x)$ 是线性分类器 $h:\bf x\mapsto w\cdot x+\Bbb b$ 点 $x$ 是其到超平面 $\bf w\cdot x+\Bbb b$ 的欧几里德距离

$$p_h(x)=\frac{|\bf w\cdot x+\Bbb b|}{||\bf w||_2}.(5.4)$$

样本 $S=(x_1，…，x_m)$ 的线性分类器 $h$ 的几何余量 $p_h$ 是样本中各点的最小几何余量 $ρ_h=min_{i\in[m]} ρ_h(x_i)$，即定义 $h$ 的超平面到最近采样点的距离。
SVM解是具有最大几何余量的分离超平面，因此称为最大余量超平面。图5.1的右面板显示了SVM返回的最大边距超平面可分离情况下的算法。我们将在本章后面介绍一种理论，为这种解决方案提供有力的理由。然而，我们已经可以观察到，SVM解决方案也可以被视为以下意义上的“最安全”选择：测试点通过具有几何边界ρ的分离超平面正确分类，即使它位于共享相同标签的训练样本的距离 $ρ$ 之内；对于SVM解决方案， $ρ$ 是最大几何裕度，因此是“最安全”的值。

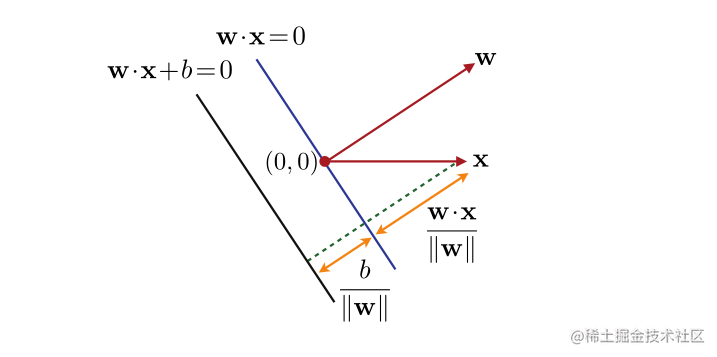
图5.2

在 $\bf w·x>0$ 和 $\Bbb b>0$ 的情况下，点 $\bf x$ 的几何边界的图示。

5.2.1原始优化问题

我们现在导出定义SVM解决方案的方程和优化问题。根据几何边界的定义（见图5.2），分离超平面的最大边界 $ρ$ 如下所示：

$$p=\underset {\bf w,\Bbb b:\Bbb y_{\Bbb i}(\bf w\cdot x_{\Bbb i}+\Bbb b)\ge 0}{max}\underset {i\in[m]}{min}\frac{|\bf w\cdot x_{\Bbb i}+\Bbb b|}{||\bf w||}=\underset {\bf w,\Bbb b}{max}\underset {i\in[m]}{min}\frac{y_i(\bf w\cdot x_{\Bbb i}+\Bbb b)}{||\bf w||}.(5.5)$$

第二个等式来自这样一个事实：由于样本是线性可分的，对于最大化对 $(\bf w,\Bbb b)$ ， $y_i(\bf w·x_i+\Bbb b)$ 对于所有 $i\in [m]$ 必须是非负的 。现在，观察最后一个表达式对于 $(\bf w,\Bbb b)$ 乘以正标量是不变的。因此，我们可以将自己限制在成对 $(\bf w,\Bbb b)$ 的范围内，以便 $min_{i\in [m]} y_i(\bf w·x_{\Bbb i}+\Bbb b)=1$：

$$p=\underset {\underset{min_{i\in [m]y_i(\bf w\cdot x_{\Bbb i}+\Bbb b)=1}}{\bf w,b:}}{max}\frac{1}{||\bf w||}=\underset {\underset {\forall i\in [m],y_i(\bf w\cdot x_{\Bbb i}+\Bbb b)\ge 1}{\bf w,b:}}{max}\frac{1}{||\bf w||}.(5.6)$$

第二个等式是因为对于最大化对 $(\bf w,\Bbb b)$ ， $y_i(\bf w·x_{\Bbb i}+\Bbb b)$ 的最小值为 $1$ 。

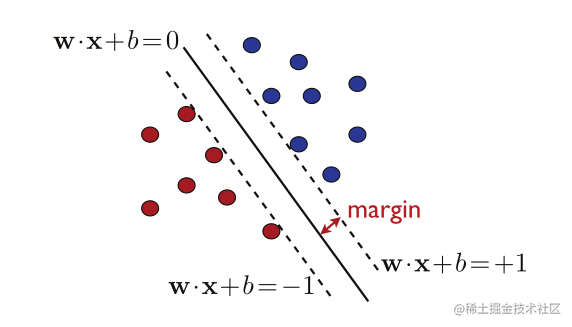
图5.3

(5.6) 的最大边界超平面解。图上的虚线表示边缘超平面。

图5.3说明了最大化(5.6)的解决方案 $(\bf w, \Bbb b)$ 。除了最大边缘超平面，它还显示了边缘超平面，这是平行于分离超平面，并通过最近的点在正或负的一面。由于它们平行于分离超平面，因此它们承认相同的法向量 $\bf w$ 。而且，由于最近点的 $|\bf w·x+\Bbb b| = 1$ ，因此边缘超平面的方程为 $\bf w·x+\Bbb b =±1$
由于最大化 $1/||\bf w||$ 相当于最小化 $\frac{1}{2}||\bf w||^2$ ，鉴于（5.6），SVM在可分离情况下返回的对 $(\bf w, \Bbb b)$ 是以下凸优化问题的解：

$$\begin{aligned} &\underset {\bf w, \Bbb b}{min}\frac{1}{2}||\bf w||^2\\ &受y_i(w\cdot x+\Bbb b)\ge \Bbb1,\forall \Bbb i\in [\Bbb m].的影响。(5.7) \end{aligned}$$

目标函数 $F:\bf w\mapsto \frac{1}{2}||\bf w||^2$ 是无限可微的。它的梯度是 $\nabla F(\bf w)=w$ ，其Hessian为单位矩阵 $\nabla^2 F(\bf w)=I$ ，其特征值为严格正。因此 $\nabla^2 F(\bf w)\succ 0$ 和 $F$ 是严格凸的。这些约束都是由仿射函数 $g_i：(\bf w，\Bbb b)\mapsto1-y_i(\bf w\cdot x+\Bbb b)$ 定义的，因此符合资格。因此，鉴于已知的凸优化结果（详见附录B），第（5.7）节中的优化问题有一个唯一的解决方案，这是一个重要且有利的特性，并不适用于所有学习算法。
此外，由于目标函数是二次函数且约束是仿射的，所以（5.7）的优化问题实际上是二次规划（ $QP$）的一个具体实例，这是优化中广泛研究的一类问题。各种商业和开源解算器可用于解决凸 $QP$问题。此外，由于支持向量机在经验上的成功以及其丰富的理论基础，已经开发出专门的方法来更有效地解决这个特殊的凸 $QP$问题，特别是具有两个坐标块的块坐标下降算法。

5.2.2支持向量

回到优化问题（5.7），我们注意到约束是仿射的，因此是合格的。目标函数和仿射约束是凸的和可微的。因此，定理B.30的要求和KKT条件适用于最佳情况。我们将使用这些条件来分析该算法并演示其几个关键特性，然后在第5.2.3节中导出与支持向量机相关的对偶优化问题。
我们引入拉格朗日变量 $\alpha\ge 0$ ， $i\in [m]$ ，与 $m$ 约束相关，并用 $\alpha$ 表示向量 $(\alpha_1，…，\alpha_m)$。然后可以为所有 $\bf w\in \mathbb R^N$ ， $b\in \mathbb R$、 和 $\alpha\in \mathbb R^m_+$ 定义拉格朗日，通过

$$\mathcal L(\bf w,b,\alpha)=\frac{1}{2}||\bf w||^2-\sum^m_{\Bbb i=1}\alpha_{\Bbb i}[\Bbb y_\Bbb i(w\cdot x+\Bbb b)-\Bbb 1].(5.8)$$

通过将拉格朗日关于原始变量 $\bf w$ 和 $b$ 的梯度设置为零，并写入互补条件，可获得KKT条件：

$$\begin{aligned} \nabla_{\bf w}\mathcal L={\bf w}-\sum^m_{i=1}\alpha_iy_i\bf x_\Bbb i=0 \qquad&\Longrightarrow\qquad {\bf w} =\Bbb {\sum^m_{i=1}\alpha_i\Bbb y_i\bf x_\Bbb i}(5.9)\\ \nabla_{b}\mathcal L=-\sum^m_{i=1}\alpha_iy_i=0\qquad&\Longrightarrow\qquad \sum^m_{i=1}\alpha_iy_i=0(5.10)\\ \forall i,\alpha_i[y_i(\bf w\cdot x +\Bbb b)-\Bbb 1]=0\qquad&\Longrightarrow\qquad\alpha_i=0y_i(\bf {w\cdot x} +\Bbb b)-\Bbb 1).(5.11) \end{aligned}$$

根据等式（5.9），SVM问题解的权重向量 $\bf w$ 是训练集向量 $\bf x_1,…,x_m.$ 的线性组合，当 $\alpha_i\neq 0$ 时，在该展开式中出现一个向量 $\bf x_i$ 。这种向量称为支持向量。根据互补条件（5.11），如果 $\alpha_i\neq 0$ ，则 $y_i(\bf w·x_\Bbb i+\Bbb b)=\Bbb 1$。因此，支持向量位于边缘超平面 $(\bf w·x_\Bbb i+\Bbb b)\pm\Bbb 1$上。
支持向量完全定义了最大裕度超平面或SVM解决方案，这证明了算法的名称。根据定义，不在边缘超平面上的向量不会影响这些超平面的定义-如果没有这些超平面，SVM问题的解决方案将保持不变。注意，虽然SVM问题的解 $\bf w$ 是唯一的，但支持向量不是唯一的。在尺寸 $N$ 中， $N+1$ 点足以定义超平面。因此，当超过 $N+1$ 个点位于边缘超平面上时， $N+1$ 支持向量可能有不同的选择。

5.2.3对偶优化问题