【机器学习｜数学基础】Mathematics for Machine Learning系列之线性代数（8）：矩阵的初等变换

小知识，大挑战！本文正在参与“程序员必备小知识”创作活动。

前言

Hello！小伙伴！

非常感谢您阅读海轰的文章，倘若文中有错误的地方，欢迎您指出～

自我介绍 ଘ(੭ˊᵕˋ)੭

昵称：海轰

标签：程序猿｜C++选手｜学生

简介：因C语言结识编程，随后转入计算机专业，有幸拿过一些国奖、省奖...已保研。目前正在学习C++/Linux/Python

学习经验：扎实基础 + 多做笔记 + 多敲代码 + 多思考 + 学好英语！

机器学习小白阶段

文章仅作为自己的学习笔记 用于知识体系建立以及复习

知其然 知其所以然！

若查看数学公式不全或显示错误

可以查看：MML学习笔记（八）：线性代数之矩阵的初等变换

3.1 矩阵的初等变换

定义

矩阵的初等行变换

1. 对调两行（对调i，j两行，记作 $r_{i}\leftrightarrow r_{j}$）
2. 以数 $k\neq 0$乘某一行中的所有元素（第i行乘以k，记作 $r_{i}×k$）
3. 把某一行所有的元素的k倍加到另一行对应的元素上（第j行的k倍加到第i行上，记作 $r_{i}+kr_{j}$）

列变换同理，对列进行相应的操作（也是上面三种操作） ​ 初等行变换、列变换统称初等变换。 如果矩阵A经过有限次初等行变换变成B，就称矩阵A与B行等价，记作 $A\stackrel{r}{\sim}B$

如果矩阵A经过有限次初等列变换变成B，就称矩阵A与B列等价，记作 $A\stackrel{c}{\sim}B$

如果矩阵A经过有限次初等变换变成矩阵B，那么称矩阵A与B等价，记作 $A～B$

注：

后文中使用如下符号代表行、列变换   $A\stackrel{r}{\sim}B代表A通过 列 变换到B$ $A\stackrel{c}{\sim}B 代表A通过 列 变换到B$

等价具有的性质

矩阵之间的等价关系具有以下性质：

1. 反身性 $A～A$
2. 对称性 若 $A～B$，则 $B～A$
3. 传递性 若 $A～B，B～C$，则 $A～C$

矩阵类型

1、行阶梯形矩阵

可以画出一条阶梯线，线的下方全为0； 每一个台阶只有一行，台阶数即是非零行的行数，阶梯线的竖线后面的第一个元素为非零元，也就是非零行的第一个非零元。

2、行最简形矩阵

在行阶梯形矩阵定义的基础之上还要求：

• 非零行的第一个非零元为1​
• 且这些非零元所处的列的其他元素为0.

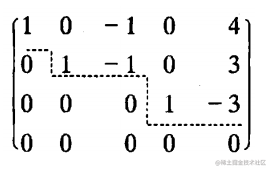任何矩阵 $A_{m×n}$总可经过有限次初等变换将其变为行阶梯形矩阵、行最简形矩阵。

3、标准形矩阵

对行最简形矩阵再进行处等列变换，可以得到一种形状更简单的矩阵，成为标准形矩阵。 其特点是左上角是一个单位矩阵，其余元素均为0.

对于矩阵A，总可以经过一系列初等变换转化为标准形矩阵F ​ 其中r为行阶梯形矩阵中非零行的行数。

4、初等矩阵

由单位矩阵E经过一次初等变换得到的矩阵称为初等矩阵

有三种初等变换，则有三种初等矩阵，下面以行初等变换为例 ​ （1）将单位矩阵中的第i、j行对调，得初等矩阵 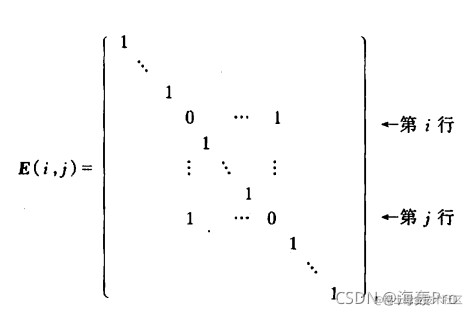用m阶初等矩阵 $E_m(i,j)$左乘矩阵A，其中 $A=(a_{ij})_{m*n}$，得到 ​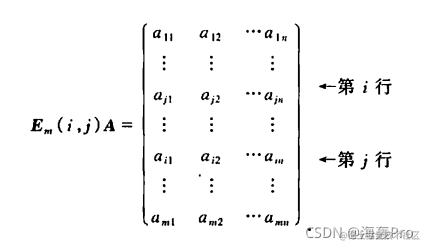

观察结果，可以发现最终结果其实就是将A矩阵中第i、j行进行了对调 $（r_i \leftrightarrow r_j）$

举个实际例子（左乘）： ​ 对调单位矩阵的第1、3行

同理，以n阶初等矩阵右乘矩阵A，结果就是相对于对矩阵A进行列变换 ​ （2）以数 $k!=0$乘单位矩阵的第i行（或第i列），得到初等矩阵 ​

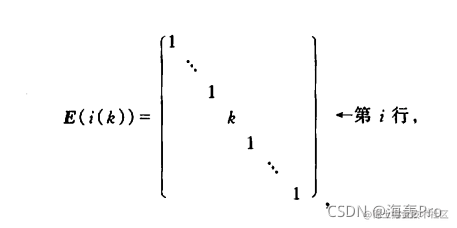
可以发现，矩阵 $E_m(i(k))$左乘矩阵A，结果就是相对于数k乘以A的第i行

举个实际例子（左乘）：

单位矩阵第二行乘以k=2

同理， $E_m(i(k))$右乘A，相当于k乘以A的第i列 ​ （3）以k乘E的第j行加到第i行（或k乘以第j列加到第i列），得到初等矩阵 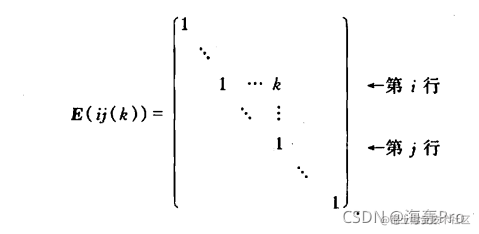左乘时，相当于把矩阵A的第j行乘k加到第i行上

举个实际例子（左乘）：

单位矩阵第3行乘以k=2加到第2行上

同理，右乘时，相当于把矩阵A的第j列乘k加到第i列上

性质

从上面的讨论中，可以得出

性质1

设A是一个m*n矩阵

• 对A施加一次初等行变换，相当于在A的左边乘以相应的m阶初等矩阵；
• 对A施加一次初等列变换，相当于在A的右边乘以相应的n阶初等矩阵

初等矩阵都是可逆的，且其逆矩阵都是同一类型的初等矩阵

• $E(i,j)^{-1} = E(i,j)$
• $E(i(k))^{-1}=E(i(\frac{1}{k}))$
• $E(ij(k))^{-1}=E(ij(-k))$

注意

• $E(i(k))是指对单位矩阵第i行乘以k$
• $E(ij(k))是指单位矩阵第i行 加上 第j行乘以k$

实例演示 ​ 设3阶单位阵E ​

$$E=\begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{bmatrix}$$

很显然

• (E)E=E
• E(E)=E

​

所以单位阵的逆矩阵为其本身 即 $E(i,j)^{-1} = E(i,j)$

假设对E的第二行乘以2 ​ 得到 $E(i(2)) =\begin{bmatrix} 1 & 0 & 0\\ 0 & 2 & 0\\ 0 & 0 & 1 \end{bmatrix}(i = 2，表示第二行)$

那么 $E(i(2))^{-1}=E(i(\frac{1}{2})) =\begin{bmatrix} 1 & 0 & 0\\ 0 & \frac{1}{2} & 0\\ 0 & 0 & 1 \end{bmatrix}$ ​

有

$$\begin{bmatrix} 1 & 0 & 0\\ 0 & 2 & 0\\ 0 & 0 & 1 \end{bmatrix} * \begin{bmatrix} 1 & 0 & 0\\ 0 & \frac{1}{2} & 0\\ 0 & 0 & 1 \end{bmatrix}=\begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{bmatrix} = E$$

​

假设对E的第3行乘以2 再加到第2行上 ​

得到 $E(ij(2)) = \begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & 2\\ 0 & 0 & 1 \end{bmatrix}(i=2、j = 3，分别表示第2、3行)$

那么 $E(ij(2))^{-1} = E(ij(-2)) = \begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & -2\\ 0 & 0 & 1 \end{bmatrix}$

有

$$​ \begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & -2\\ 0 & 0 & 1 \end{bmatrix} + \begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & 2\\ 0 & 0 & 1 \end{bmatrix}= \begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{bmatrix}=E$$

性质2

方阵A可逆的充分必要条件是存在有限个初等矩阵 $P_1,P_2,...P_i,$使得 $A=P_1P_2...P_i$ ​ 证明：

先证明充分性：

设 $A=P_1P_2...P_i$

因为初等矩阵可逆，有限个可逆矩阵的乘积依然可逆

所以A可逆

证必要性：

假设n阶方阵A可逆

A通过一系列变换转换为标准形矩阵F

那么F也可以通过一系列初等变换转换为A ​ $F～A$

所以 ​ $A=P_1...P_sFP_{s+1}...P_i$ ​ 因为A可逆， $P_1,P_2,...P_i,$也可逆 ​ 所以F也可逆 ​ 又因为 ​ $F=\begin{bmatrix} E_r & 0\\ 0 & 0 \end{bmatrix}_{n*n}$ ​ 若r<n ​ 那么｜F｜=0 说明F不可逆 与前提条件相反 ​ 所以r=n ​ 即F=E（F为单位矩阵） ​ 所以

$A=P_1P_2...P_i$

定理1

设A、B均为m×n矩阵，那么

1. $A～B(r)$【指对A进行初等行变换】的充分必要条件是存在m阶可逆矩阵P，使得 $PA=B$
2. $A～B(c)$【指对A进行初等列变换】的充分必要条件是存在n阶可逆矩阵Q，使得 $AQ=B$
3. $A～B$的充分必要条件是存在m阶可逆矩阵P、n阶可逆矩阵Q，使得 $PAQ=B$

推论

方阵A可逆的条件是 $A～E(r,指行变换)$

证明充分性：

因为 $A～E(r,指行变换)$

所以存在初等矩阵P，使得 $PA=E$

因为E可逆、 P可逆 ​ 那么A一定可逆 ​ 证明必要性： ​ 首先A通过初等行变换一定可以变为F A～F ​

$$F=\begin{bmatrix} E_r & 0\\ 0 & 0 \end{bmatrix}_{n*n}$$

若r<n 说明|F|=0 ​ 因为A可逆 所以F可逆 ​ 若|F|=0 则不可逆 ​ 所以|F|！=0 ​ 那么 r=n ​ 即 F=E ​ 故 $A～E(r,指行变换)$

补充

定理1表明，如果 $A～B(r,指行变换)$，即A经过一系列初等行变换可以变为B，则一定存在可逆矩阵P，使得 $PA=B$，那么如何求P呢？ ​ 假设已知A、B的情况下 ​ 首先依据题意可得 ​

$$\begin{cases} PA=B\\ PE=P \end{cases}$$

所以

$P(A,E)=(B,P)$

推出 ​ 矩阵(A,E)通过初等行变换可以变为矩阵(B,P) ​ A、E、B已知，那么P就一目了然啦 ​ 注意： 矩阵(A,E)的意思是矩阵A与矩阵E横行拼接 ​ 比如

$$A=\begin{bmatrix} 1 & 2\\ 3 & 4 \end{bmatrix}$$

$$E=\begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix}$$

那么矩阵

$$(A,E)=\begin{bmatrix} 1 & 2 & 1 & 0\\ 3 & 4 & 0 & 1 \end{bmatrix}$$

当B=E时，此时求的P就是A的逆矩阵 $A^{-1}$（求逆矩阵的一个常用方法！）

结语

说明：

• 参考于 课本《线性代数》第五版 同济大学数学系编
• 配合书中概念讲解 结合了自己的一些理解及思考

文章仅作为学习笔记，记录从0到1的一个过程

希望对您有所帮助，如有错误欢迎小伙伴指正～

我是 海轰ଘ(੭ˊᵕˋ)੭

如果您觉得写得可以的话，请点个赞吧

谢谢支持 ❤️