神经网络学习笔记——反向传播

这是我参与11月更文挑战的第7天

反向传播 backpropagation —— 一种快速计算代价函数梯度的算法

使⽤矩阵快速计算输出

为了解释问题，首先给出神经网络中权重的清晰定义，如下图所示：

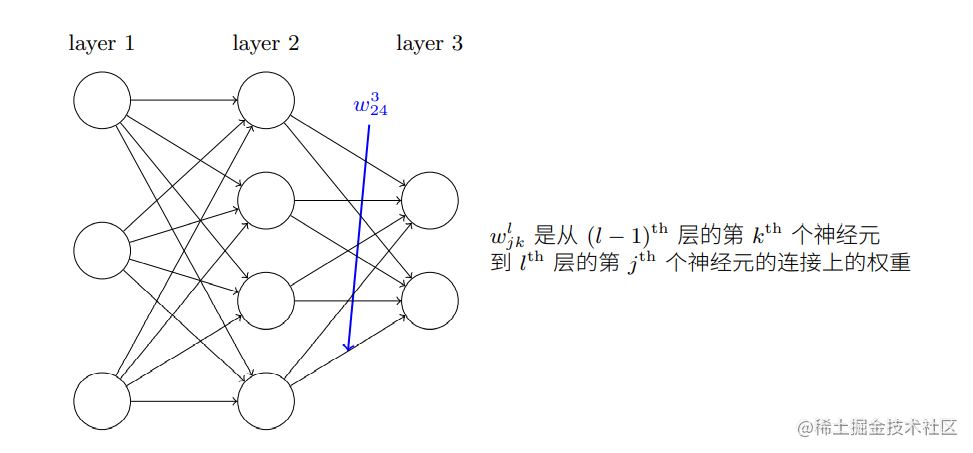
同样定义 $b^l_j$为第 $l$层的第 $j$个神经元的偏置：

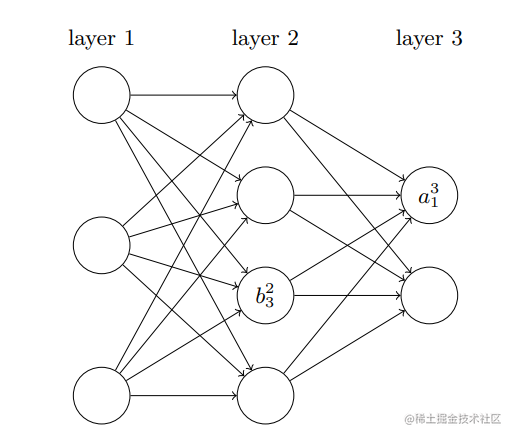
基于上面的定义，可以得到第 $l$层的第 $j$个神经元的激活值 $a^l_j$（这个值和第 $l-1$层的激活值 $a^{l-1}_k$有关）：

$$a^l_j=\sigma(\sum_kw^l_{jk}a^{l-1}_k+b^l_j)$$

其中 $\sum_kw^l_{jk}a^{l-1}_k$中的 $k$表示 $l-1$层中的所有神经元数量，对于每一层 $l$定义一个权重矩阵 $w^l$， $w^l$中的元素是 $l-1$层到 $l$层连接的权重，因此 $w^l_{jk}$可以理解为 $l-1$层中第 $k$个神经元到 $l$层第 $j$个神经元的连接权重。

上面的公式可以简化为：

$$a^l=\sigma(w^la^{l-1}+b^l)$$

在计算 $a^l$需要计算中间量 $z^l=w^la^{l-1}+b^l$，将 $z^l$称为 $l$层神经元的带权输入，因此上面的公式又可以简化为 $a^l=\sigma(z^l)$。

代价函数的两个假设

反向传播算法的目标是计算代价函数 $C$关于两个参数 $w$和 $b$的偏导数 $\frac{\partial C}{\partial w},\frac{\partial C}{\partial b}$。将 $C$定义为一个二次代价函数：

$$C=\frac{1}{2n}\sum_x||y(x)-a^L(x)||^2$$

$n$表示训练样本总数， $\sum_x$表示遍历了所有样本， $y=y(x)$是输入 $x$时对应的期望目标输出， $L$表示网络层数， $a^L=a^L(x)$是当输入为 $x$时网络输出的激活值向量。

为了应用反向传播算法，要对代价函数 $C$做两个假设：

• 代价函数可以被写成一个在每个训练样本 $x$上的代价函数 $C_x$的均值 $C=\frac{1}{n}\sum_xC_x$，其中每个独立样本的代价为 $C_x=\frac{1}{2}||y-a^L||^2$。
• 代价函数可以写成神经网络的输出函数： $cost\ C = C(a^L)$，在这个假设下 $C_x$可以进一步写成：

$$C=\frac{1}{2}||y-a^L||^2=\frac{1}{2}\sum_j(y_j-a^L_j)^2$$

背景知识 hadamard乘积/schur乘积： $s\odot t$

$s\odot t$表示按元素乘积， $(s\odot t)_j=s_jt_j$，如下所示：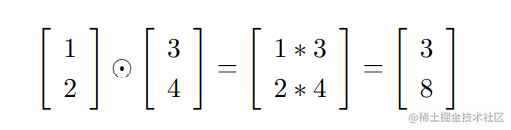

微分、梯度和梯度下降的关系

四个基本公式

反向传播算法的核心是计算偏导数 $\frac{\partial C}{\partial w^l_{jk}},\frac{\partial C}{\partial b^l_j}$，为达目的首先引入中间量 $\delta^l_j$，表示第 $l$层第 $j$个神经元上的误差：

$$\delta^l_j=\frac{\partial C}{\partial z^l_j}$$

这个公式基于一个启发式的认识，即 $\frac{\partial C}{\partial z^l_j}$是神经元误差的度量。

反向传播基于四个基本公式，这些公式让我们可以计算误差和代价函数梯度。

公式1

输出层误差 $\delta^L$的公式：

$$\delta^L_j=\frac{\partial C}{\partial a^l_j}\sigma'(z^L_j) \tag{1}$$

公式中 $\frac{\partial C}{\partial a^l_j}$表示代价 $C$随着第 $l$层第 $j$个神经元输出的激活值的变化而变化的速率， $\sigma'(z^L_j)$表示激活函数 $\sigma$在 $z^L_j$处的变化速率。对于二次代价函数 $C=\frac{1}{2}\sum_j(y_j-a_j)^2$， $\frac{\partial C}{\partial a^l_j}=(a_j-y_j)$。

为方便计算将公式（1）重写为矩阵形式：

$$\delta^L=\nabla_aC\odot\sigma'(z^L)$$

带入二次代价函数的偏导计算得到：

$$\delta^L=(a^L-y)\odot\sigma'(z^L)$$

公式2

使用下一层的误差 $\delta^{l+1}$来表示当前层的误差 $\delta^l$：

$$\delta^l=((w^{l+1})^T\delta^{l+1})\odot\sigma'(z^l) \tag{2}$$

公式（2）给出了由下一层误差推导当前层误差的方法，这就是反向传播中反向的含义，即可以将其看作沿着⽹络反向移动误差，通过组合公式（1）和公式（2）可以实现计算任意层的误差。

公式3

代价函数和网络中任意偏置相关的变化率：

$$\frac{\partial C}{\partial b^l_j}=\delta^l_j \tag{3}$$

公式（3）证明误差 $\delta^l_j$和偏导数值 $\frac{\partial C}{\partial b^l_j}$完全一致。

公式4

代价函数和任何一个权重相关的变化率：

$$\frac{\partial C}{\partial w^l_{jk}}=a^{l-1}_k\delta^l_j \tag{4}$$

公式（4）给出了偏导数 $\frac{\partial C}{\partial w^l_{jk}}$的计算方法，它可以简化为：

$$\frac{\partial C}{\partial w}=a_{in}\delta_{out}$$

$a_{in}$表示权重为 $w$的链路上的输入激活值， $\delta_{out}$表示权重为 $w$链路上的输出误差，如下图所示：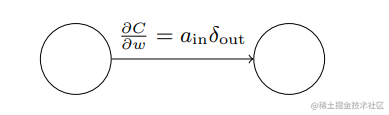

S型函数的特征令 $\sigma$在接近0或1时变化会非常小，这也会让权重学习变得缓慢，对于这样的情形，称为输出神经元已经饱和了，继而权重学习会终⽌（或者学习⾮常缓慢），从上面的公式可以看出学习的速率和 $\sigma'$有关。

四个公式的证明

背景知识

多元微积分链式法则公式：

$$\frac{dw}{dt}=\sum^n_{i=1}\frac{\partial w}{\partial x_i}\frac{dx_i}{dt}$$

公式1证明

回忆输出误差 $\delta$的定义：

$$\delta^L_j=\frac{\partial C}{\partial z^L_j}$$

基于上述背景知识可以将公式1改写为：

$$\delta^L_j =\sum_k \frac{\partial C}{\partial a^L_k}\frac{\partial a^L_k}{\partial z^L_j}$$

$k$表示输出层的所有神经元，第 $k$个神经元的 $a^L_k$只依赖于 $k=j$时的输入权重 $z^L_j$，也就是说 $k \neq j$时 $\frac{\partial a^L_k}{\partial z^L_j}$不存在，基于前面的理论，上面的公式可以化为：

$$\delta^L_j = \frac{\partial C}{\partial a^L_j}\frac{\partial a^L_j}{\partial z^L_j}$$

基于 $a^L_j=\sigma(z^L_j)$上面公式的右边可以写为 $\sigma'(z^L_j)$，因此可以得到公式1：

$$\delta^L_j=\frac{\partial C}{\partial a^l_j}\sigma'(z^L_j) \tag{1}$$

公式2证明

继续延伸误差 $\delta$：

$$\delta^l_j=\frac{\partial C}{\partial z^l_j}$$

依旧用链式法则，公式2的核心思想是用下一层误差表示当前误差，因此要想办法引入 $\delta^{l+1}_k$，而 $\delta^{l+1}_k=\frac{\partial C}{\partial z^{l+1}_j}$，显然要想办法引入 $\partial z^{l+1}_j$到误差公式中：

$$\delta^l_j=\frac{\partial C}{\partial z^l_j} =\sum_k \frac{\partial C}{\partial z^{l+1}_k}\frac{\partial z^{l+1}_k}{\partial z^{l}_j}=\sum_k \frac{\partial z^{l+1}_k}{\partial z^{l}_j} \delta^{l+1}_k$$

由 $z$的定义可得：

$$z^{l+1}_k=\sum_jw^{l+1}_{kj}a^l_j+b^{l+1}_k=\sum_j w^{l+1}_{kj}\sigma(z^l_j)+b^{l+1}_k$$

计算 $\frac{\partial z^{l+1}_k}{\partial z^{l}_j}$得到：

$$\frac{\partial z^{l+1}_k}{\partial z^{l}_j}=w^{l+1}_{kj}\sigma'(z^l_j)$$

计算过程可以用数学归纳法证明，过程如下：

当 $j=1$时：

$$\frac{\partial z^{l+1}_k}{\partial z^{l}_1}=w^{l+1}_{k1}\sigma'(z^l_1)$$

当 $j=2$时：

$$\frac{\partial z^{l+1}_k}{\partial z^{l}_2}=w^{l+1}_{k2}\sigma'(z^l_2)$$

当 $j=m$时：

$$\frac{\partial z^{l+1}_k}{\partial z^{l}_m}=w^{l+1}_{km}\sigma'(z^l_m)$$

证明完毕

综合上述公式可以得到公式2：

$$\delta^l_j=\sum_k w^{l+1}_{kj}\delta^{l+1}_k\sigma'(z^l_j)= ((w^{l+1})^T\delta^{l+1})\odot\sigma'(z^l)$$

公式3的证明

$$\frac{\partial C}{\partial b^l_j}=\frac{\partial C}{\partial z^l_j}\frac{\partial z^l_j}{\partial b^l_j}=\delta^l_j \times 1$$

公式4证明

$$\frac{\partial C}{\partial w^l_{jk}}=\frac{\partial C}{\partial z^l_{j}}\frac{\partial z^l_{j}}{\partial w^l_{jk}}=\delta^l_j\frac{\partial (\sum_k w^l_{jk}a^{l-1}_k+b^l_j)}{\partial w^l_{jk}}=a^{l-1}_k\delta^l_j$$

反向传播算法过程

• 输入x：为输入层设置激活值 $a^1$
• 前向传播：对于从第二层开始的 $l=2,3,4...,L$计算中间值 $z^l=w^la^{l-1}+b^l$和 $a^l=\sigma(z^l)$
• 输出层误差 $\delta^L$：计算最后一层（输出层）误差 $\delta^L=\nabla_aC\odot\sigma'(z^L)$
• 反向误差传播：基于 $\delta^L$逆推前面层的误差（ $l=L-1,L-2,...,2$），计算 $\delta^l=((w^{l+1})^T\delta^{l+1})\odot\sigma'(z^l)$
• 输出：计算代价函数梯度，即 $\frac{\partial C}{\partial b^l_j}=\delta^l_j$、 $\frac{\partial C}{\partial w^l_{jk}}=a^{l-1}_k\delta^l_j$。

在反向传播算法的基础上应用梯度下降方法更新参数过程：

算法的实现

# 反向传播算法
    # 返回一个元祖，nabla_b, nabla_w表示损失函数C_x的梯度
    def backprop(self,x,y):
        nabla_b = [np.zeros(b.shape) for b in self.biases]
        nabla_w = [np.zeros(w.shape) for w in self.weights]
        # feedforward 前向传播
        #设置输入层激活值activation=a^1
        #activations 用来存储每层的激活值
        activation = x
        activations = [x]
        # zs用来存储每一层的中间值z
        zs = [] #
        for b, w in list(zip(self.biases, self.weights)):
            # 中间值z的计算
            z = np.dot(w, activation) + b
            zs.append(z)
            # 基于z计算激活值
            activation = sigmoid(z)
            activations.append(activation)
        # backward pass 反向传播
        # cost_derivative 计算网络输出值和期望输出的差值 即nabla C
        # sigmoid_prime返回sigmoid函数的导数
        # 计算误差delta
        delta = self.cost_derivative(activations[-1], y) * sigmoid_prime(zs[-1])
        # 计算参数b和w的梯度
        nabla_b[-1] = delta
        nabla_w[-1] = np.dot(delta, activations[-2].transpose())
        # 从后往前（反向）逆推前面层的误差delta
        for l in range(2, self.num_layers):
            # 反向因此此处是-l
            z = zs[-l]
            sp = sigmoid_prime(z)
            delta = np.dot(self.weights[-l + 1].transpose(), delta) * sp
            # 存储对应层的nabla b和 nabla w
            nabla_b[-l] = delta
            nabla_w[-l] = np.dot(delta, activations[-l - 1].transpose())
        return nabla_b, nabla_w
复制代码