绕任意轴旋转思路
中心轴与坐标轴平行
1.将旋转轴平移与坐标轴重合,物体也做平移操作;
2.物体绕坐标轴旋转;
3.执行步骤1的逆操作,将旋转轴平移回到原来位置,物体也对应平移;
中心轴与坐标轴不平行
可以参照上节的“中心轴与坐标轴平行”的做法,只是多一个步骤,将旋转轴旋转到与任意坐标轴平行,以及后面的逆操作;
具体步骤:
1.将旋转轴平移至原点;
2.将旋转轴旋转至YOZ平面;
3.将旋转轴旋转与Z轴重合;
4.物体绕Z轴旋转 θ \theta θ度;
5.执行步骤3,步骤2,步骤1的逆操作;
计算向量 v ⃗ \vec{v} v绕向量 a ⃗ \vec{a} a旋转 θ \theta θ度
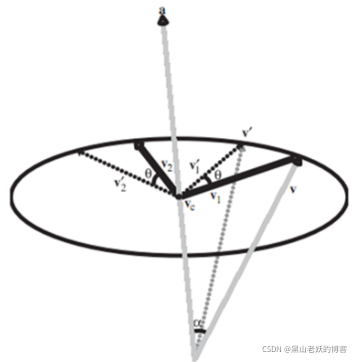
向量 v ⃗ \vec{v} v可以分解为向量 v c ⃗ \vec{v_{c}} vc与向量 v 1 ⃗ \vec{v_{1}} v1;
向量 v 1 ⃗ \vec{v_{1}} v1绕向量 a ⃗ \vec{a} a旋转 θ \theta θ度后,得到向量 v 1 ′ ⃗ \vec{v_{1}'} v1′;
我们最终的目标是计算得到向量 v ′ ⃗ = v c ⃗ + v 1 ′ ⃗ \vec{v'}=\vec{v_{c}}+\vec{v_{1}'} v′=vc+v1′;
两个向量的初始值为:
α ⃗ = { α x , α y , α z } \vec{\alpha }=\left \{ \alpha _{x} ,\alpha _{y},\alpha _{z}\right \} α={
αx,αy,αz}
v ⃗ = { v x , v y , v z } \vec{v }=\left \{ v_{x} ,v_{y},v_{z}\right \} v={
vx,vy,vz}
具体的计算步骤如下:
1.计算得到向量 v ⃗ \vec{v} v在向量 a ⃗ \vec{a} a方向上的投影为:
v c ⃗ = ( v ⃗ ⋅ α ⃗ ) ⋅ α ⃗ \vec{v_{c}}=(\vec{v}\cdot \vec{\alpha })\cdot\vec{\alpha } vc=(v⋅α)⋅α
2.计算得到向量 v 1 ⃗ \vec{v_{1}} v1:
v 1 ⃗ = v ⃗ − v c ⃗ = v ⃗ − ( v ⃗ ⋅ α ⃗ ) ⋅ α ⃗ \vec{v_{1}}=\vec{v}-\vec{v_{c}}=\vec{v}-(\vec{v}\cdot \vec{\alpha })\cdot\vec{\alpha } v1=v−vc=v−(v⋅α)⋅α
由于 α ⃗ × α ⃗ = 0 \vec{\alpha }\times\vec{\alpha }=0 α×α=0,则 v 2 ⃗ \vec{v_{2}} v2可以计算得到下式:
v 2 ⃗ = v 1 ⃗ × α ⃗ = ( v ⃗ − ( v ⃗ ⋅ α ⃗ ) ⋅ α ⃗ ) × α ⃗ = v ⃗ × α ⃗ − ( v ⃗ ⋅ α ⃗ ) ⋅ α ⃗ × α ⃗ = v ⃗ × α ⃗ \vec{v_{2}}=\vec{v_{1}}\times \vec{\alpha }=(\vec{v}-(\vec{v}\cdot \vec{\alpha })\cdot\vec{\alpha })\times\vec{\alpha }=\vec{v}\times\vec{\alpha }-(\vec{v}\cdot \vec{\alpha })\cdot\vec{\alpha }\times\vec{\alpha }=\vec{v}\times\vec{\alpha } v2=v1×α=(v−(v⋅α)⋅α)×α=v×α−(v⋅α)⋅α×α=v×α
3.计算得到 v ′ ⃗ \vec{v'} v′:
v ′ ⃗ = v c ⃗ + v 1 ⃗ ∗ c o s θ + v 2 ⃗ ∗ s i n θ \vec{v'}=\vec{v_{c}}+\vec{v_{1}}*cos\theta +\vec{v_{2}}*sin\theta v′=vc+v1∗cosθ+v2∗sinθ
= v c ⃗ + v 1 ⃗ ∗ C + v 2 ⃗ ∗ S =\vec{v_{c}}+\vec{v_{1}}*C +\vec{v_{2}}*S =vc+v1∗C+v2∗S
= ( v ⃗ ⋅ α ⃗ ) ⋅ α ⃗ + ( v ⃗ − ( v ⃗ ⋅ α ⃗ ) ⋅ α ⃗ ) ∗ C + v ⃗ × α ⃗ ∗ S =(\vec{v}\cdot \vec{\alpha })\cdot\vec{\alpha }+(\vec{v}-(\vec{v}\cdot \vec{\alpha })\cdot\vec{\alpha })*C+\vec{v}\times\vec{\alpha }*S =(v⋅α)⋅α+(v−(v⋅α)⋅α)∗C+v×α∗S
= v ⃗ ∗ C + ( v ⃗ ⋅ α ⃗ ) ⋅ α ⃗ ∗ ( 1 − C ) + v ⃗ × α ⃗ ∗ S =\vec{v}*C+(\vec{v}\cdot \vec{\alpha })\cdot\vec{\alpha }*(1-C)+\vec{v}\times\vec{\alpha }*S =v∗C+(v⋅α)⋅α∗(1−C)+v×α∗S
其中:C表示 c o s θ cos\theta cosθ,S表示 s i n θ sin\theta sinθ;
将组成对象坐标系的三个坐标轴,同时绕向量 a ⃗ \vec{a} a旋转 θ \theta θ度,可以得到旋转后的方向矩阵:
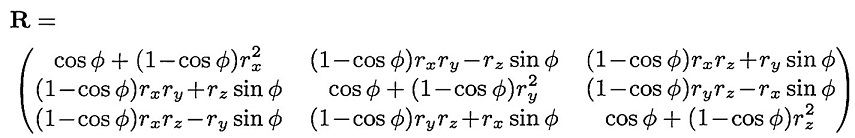
该矩阵的详细推导,参见3D数学 ---- 矩阵和线性变换(1);
VTK中的旋转计算
void vtkTransformConcatenation::Rotate(double angle, double x, double y, double z)
{
if (angle == 0.0 || (x == 0.0 && y == 0.0 && z == 0.0))
{
return;
}
// convert to radians
angle = vtkMath::RadiansFromDegrees( angle );
// make a normalized quaternion
double w = cos(0.5*angle);
double f = sin(0.5*angle)/sqrt(x*x+y*y+z*z);
x *= f;
y *= f;
z *= f;
// convert the quaternion to a matrix
double matrix[4][4];
vtkMatrix4x4::Identity(*matrix);
double ww = w*w;
double wx = w*x;
double wy = w*y;
double wz = w*z;
double xx = x*x;
double yy = y*y;
double zz = z*z;
double xy = x*y;
double xz = x*z;
double yz = y*z;
double s = ww - xx - yy - zz;
matrix[0][0] = xx*2 + s;
matrix[1][0] = (xy + wz)*2;
matrix[2][0] = (xz - wy)*2;
matrix[0][1] = (xy - wz)*2;
matrix[1][1] = yy*2 + s;
matrix[2][1] = (yz + wx)*2;
matrix[0][2] = (xz + wy)*2;
matrix[1][2] = (yz - wx)*2;
matrix[2][2] = zz*2 + s;
this->Concatenate(*matrix);
}
参考资料
1.http://www.cppblog.com/lovedday/archive/2008/01/12/41031.html
2.https://www.cnblogs.com/cg_ghost/archive/2012/04/27/2473347.html
3.http://en.wikipedia.org/wiki/Rotation_matrix#Rotation_matrix_from_axis_and_angle