二叉树（C语言实现）——顺序存储结构

/*
	二叉树顺序存储结构一般仅适合于存储完全二叉树
	 
*/
#include<stdio.h>
#include<stdlib.h>
#include<math.h>
#include<stdbool.h>
#define MaxSize 100
typedef char DataType;
typedef struct
{
	DataType data[MaxSize];	//	存储树结点的数组 
	int BiTreeNum;			//	二叉树的结点个数 
		
}SqBiTree;

void Init_BiTree(SqBiTree * T);				 //	初始化 
void Creat_BiTree(SqBiTree * T, int n);		 //	创建树 
DataType Root_BiTree(SqBiTree * T);			 //	获取根结点 
int Count_BiTree(SqBiTree * T);				 //	获取树的结点数 
int Depth_BiTree(SqBiTree * T);				 //	获取树的深度 
void Print_BiTree(SqBiTree * T);			 //	打印二叉树的结点
void PreOrder_Traverse(SqBiTree * T,int n);	 //	先序遍历二叉树 
void InOrder_Traverse(SqBiTree * T, int n);	 //	中序遍历二叉树 
void PostOrder_Traverse(SqBiTree * T, int n);//	后序遍历二叉树
void Level_Traverse(SqBiTree * T, int n);	 //	层序遍历二叉树 
bool Destroy_BiTree(SqBiTree * T);			 //	销毁二叉树 

int main()
{
	SqBiTree T;

	Init_BiTree(&T);
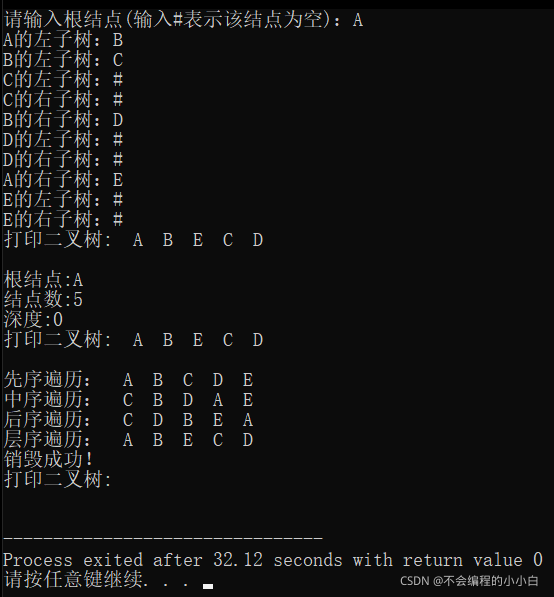
	printf("请输入根结点(输入#表示该结点为空)："); 
	Creat_BiTree(&T,1);
	printf("打印二叉树:");
	Print_BiTree(&T);
	printf("\n");
	
	printf("根结点:%c\n",Root_BiTree(&T));
	printf("结点数:%d\n", Count_BiTree(&T));
	printf("深度:%d\n",Depth_BiTree(&T));
	printf("打印二叉树:");
	Print_BiTree(&T);
	printf("\n");
	
	printf("先序遍历：");
	PreOrder_Traverse(&T,1);
	printf("\n");
	
	printf("中序遍历：");
	InOrder_Traverse(&T,1);
	printf("\n");
	
	printf("后序遍历：");
	PostOrder_Traverse(&T,1);
	printf("\n");
	
	printf("层序遍历：");
	Level_Traverse(&T, 1);
	printf("\n");
	
	if(Destroy_BiTree(&T))
		printf("销毁成功！\n");
	else
		printf("销毁失败！\n");
	printf("打印二叉树:");
	Print_BiTree(&T);
	printf("\n");
		 
	return 0;
} 

void Init_BiTree(SqBiTree * T)
{
	int i;
	for(i=0; i<MaxSize; ++i) // 清除所用内存空间的杂乱数据 
	{
		T->data[i] = '\0';
	}
	
	T->BiTreeNum = 0; 
	return; 
}

void Creat_BiTree(SqBiTree* T, int n)
{
	char ch;
	
	fflush(stdin);
	scanf("%c",&ch);
	if(ch == '#')
	{
		return;
	}
	else
	{
		T->data[n] = ch;
		T->BiTreeNum++;
		printf("%c的左子树：",ch);
		Creat_BiTree(T, 2*n);
		printf("%c的右子树：",ch);
		Creat_BiTree(T,(2*n+1));
	}
}

DataType Root_BiTree(SqBiTree * T)
{
	return T->data[1];
}

int Count_BiTree(SqBiTree * T)
{
	if(T->BiTreeNum == 0)
		return 0;
	else
		return T->BiTreeNum;
	
}

int Depth_BiTree(SqBiTree * T)
{
	if(!T)
		return 0;
	
	int k;
	pow(2,k) - 1 == T->BiTreeNum;
	return k;
}

void Print_BiTree(SqBiTree * T)
{
	int i;
	
	for(i=1; i<=T->BiTreeNum; ++i)
	{
		if(T->data[i] != '\0') 
			printf("%3c",T->data[i]);
		
	}
	printf("\n");
}

void PreOrder_Traverse(SqBiTree * T, int n)
{
	if(T->data[n] == '\0')
		return;
	else
	{
		printf("%3c",T->data[n]);
		PreOrder_Traverse(T, 2*n);
		PreOrder_Traverse(T, (2*n+1));
	}
} 

void InOrder_Traverse(SqBiTree * T, int n)
{
	if(T->data[n] == '\0')
		return;
	else
	{
		InOrder_Traverse(T, 2*n);
		printf("%3c",T->data[n]);
		InOrder_Traverse(T, (2*n+1));
	}
}

void PostOrder_Traverse(SqBiTree * T, int n)
{
	if(T->data[n] == '\0')
		return;
	else
	{
		PostOrder_Traverse(T, 2*n);
		PostOrder_Traverse(T, (2*n+1));
		printf("%3c",T->data[n]);
	}
}

void Level_Traverse(SqBiTree * T, int n)
{
	int i;
	for(i=n; i<=T->BiTreeNum; ++i)
		printf("%3c",T->data[i]);	
}
 
bool Destroy_BiTree(SqBiTree * T)
{
	T->BiTreeNum = 0;
	return true;
}