哈夫曼树（C语言实现）——最优二叉树

#include<stdio.h> 
#include<stdlib.h>
#include<stdbool.h>
#define QueueSize 100
//	哈夫曼树的结点元素类型 
typedef struct HTNode
{
	int weight;						//	权值 
	int parent, lchild, rchild;		//	双亲结点、左、右孩子结点在数组中的下标 
	
}ElemType; 
 
typedef struct
{
	ElemType * data;				//	利用数组存储哈夫曼树结点 
	int n; 							//	记录树结点的个数 
	
}HuffmanTree;
 
void Init_HuffmanTree(HuffmanTree * T, int w[], int n);	//	初始化哈夫曼树 
void Creat_HuffmanTree(HuffmanTree * T); 				//	建立哈夫曼树 
int* Select_MinIndex(HuffmanTree * T);					//	挑选权值最小的两个根结点下标 
void Print_HuffmanTree(HuffmanTree * T);				//	打印哈夫曼树 
void PreOrder_Traverse(HuffmanTree * T, int index);		//	前序遍历哈夫曼树 
void InOrder_Traverse(HuffmanTree * T, int index);		//	中序遍历哈夫曼树 
void PostOrder_Traverse(HuffmanTree * T, int index);	//	后序遍历哈夫曼树 
void Level_Traverse(HuffmanTree * T, int index);		//	层序遍历哈夫曼树 
bool Destroy_HuffmanTree(HuffmanTree * T);				//	销毁哈夫曼树 

int main()
{
	int n;
	HuffmanTree T;
	int w[250] = {2,3,4,5};
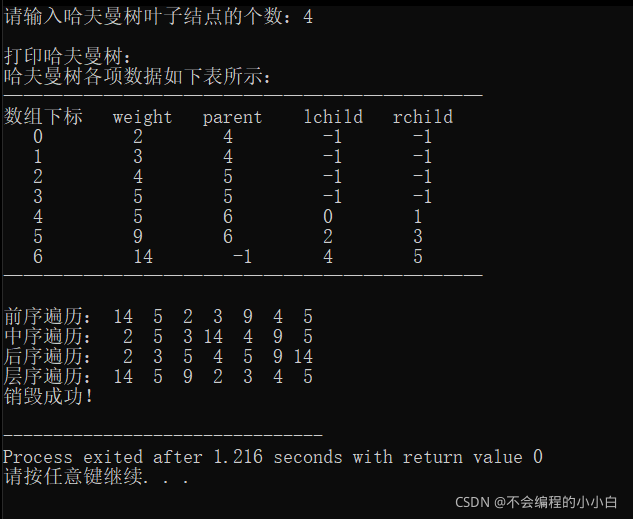
	printf("请输入哈夫曼树叶子结点的个数：");
	scanf("%d",&n);
	Init_HuffmanTree(&T, w, n);
	Creat_HuffmanTree(&T);
    printf("\n");
	printf("打印哈夫曼树：");
	Print_HuffmanTree(&T);
	
	printf("前序遍历：");
	PreOrder_Traverse(&T, T.n-1);		//	数组下标越大，权值越大，越靠近根结点 
	printf("\n");
	
	printf("中序遍历："); 
	InOrder_Traverse(&T, T.n-1);
	printf("\n");
	
	printf("后序遍历：");
	PostOrder_Traverse(&T, T.n-1);
	printf("\n");
	
	printf("层序遍历："); 
	Level_Traverse(&T,T.n-1);
	printf("\n");
	
	if(Destroy_HuffmanTree(&T))
		printf("销毁成功！\n");
	else
		printf("销毁失败！\n");
	
	return 0;
}
 
void Init_HuffmanTree(HuffmanTree * T, int w[], int n)
{
	int i;
	T->data = (ElemType*)malloc(sizeof(ElemType)*(2*n-1));	//	动态分配数组存储空间 
	T->n = n;
	 
	//	构造n棵只有根结点的树
	for(i=0; i<n; i++)
		T->data[i].weight = w[i];
	 
	for(i=0; i<2*n-1; ++i)
	{
	//	初始化，所有结点都没有双亲和左、右孩子	
		T->data[i].parent = -1;
		T->data[i].lchild = -1;
		T->data[i].rchild = -1;
	}	
}
 
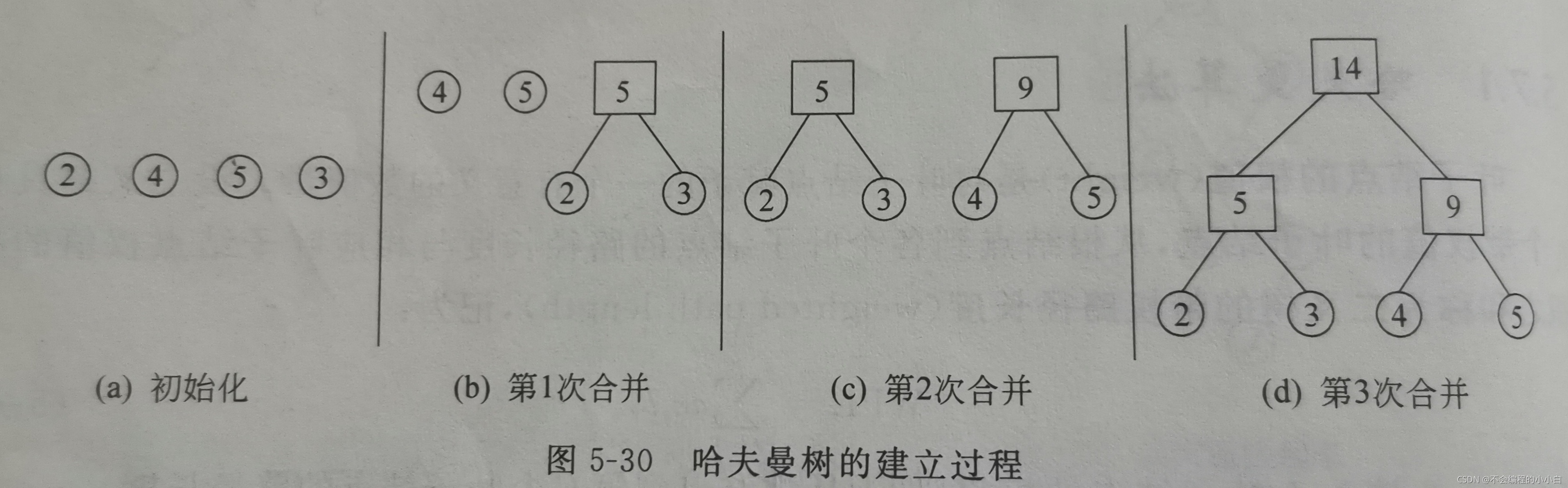
void Creat_HuffmanTree(HuffmanTree * T)
{
	int k;
	int n = T->n;
	int m = 2*n-1;
	
	for(k=n; k<m; ++k)	//	n-1次合并 
	{
		int * res = Select_MinIndex(T);	//	求出权值最小的两个下标 
		int index1 = res[0];
		int index2 = res[1];
		T->data[k].weight = T->data[index1].weight + T->data[index2].weight;
		T->data[k].lchild = index1;
		T->data[k].rchild = index2;
		T->data[index1].parent = k;
		T->data[index2].parent = k;
		T->n++;	
	}
	
	return ;
}
 
int* Select_MinIndex(HuffmanTree * T)
{
	int i;
	int firstindex,secondindex;
	int firstmin = 1000;
	int secondmin = 1000;
	
	for(i=0; i<T->n; ++i)
	{
		if(T->data[i].parent == -1)
		{
			if(T->data[i].weight<firstmin)
			{
				firstmin = T->data[i].weight;
				firstindex = i;
			}
		}
	} 
	
	for(i=0; i<T->n; ++i)
	{
		if(T->data[i].parent == -1)
		{
			if(T->data[i].weight<secondmin && T->data[i].weight!=firstmin)
			{
				secondmin = T->data[i].weight;
				secondindex = i;
			}
		}
	} 
	
	int * res = (int*)malloc(sizeof(int)*2);
	res[0] = firstindex;
	res[1] = secondindex;
	return res;
} 
 
void Print_HuffmanTree(HuffmanTree * T)
{
	int i;
	 
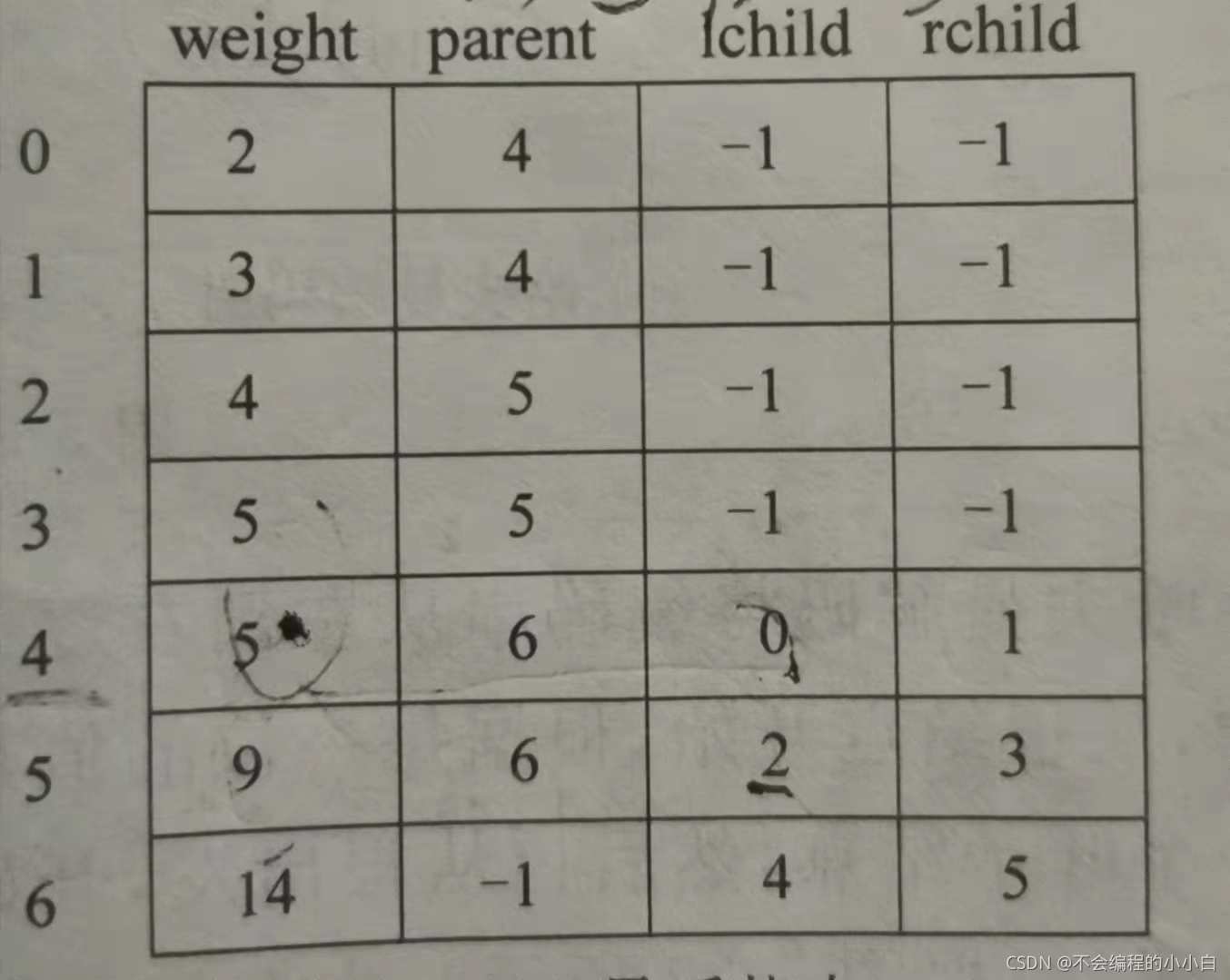
	printf("\n哈夫曼树各项数据如下表所示：\n");
	printf("————————————————————————\n");
	printf("数组下标   weight   parent    lchild   rchild\n");
	for(i=0; i<T->n-1; ++i)
	{
		printf("   %d         %d        %d	        %d	 %d\n",i,T->data[i].weight,T->data[i].parent,T->data[i].lchild,T->data[i].rchild);
	}
	printf("   %d         %d        %d	%d        %d\n",i,T->data[i].weight,T->data[i].parent,T->data[i].lchild,T->data[i].rchild);
 	printf("————————————————————————\n\n");
}
 
void PreOrder_Traverse(HuffmanTree * T, int index)
{
	if(index != -1) 
	{
		printf("%3d", T->data[index].weight);
		PreOrder_Traverse(T, T->data[index].lchild);
		PreOrder_Traverse(T, T->data[index].rchild);
	}
} 
 
void InOrder_Traverse(HuffmanTree * T, int index)
{
	if(index != -1)
	{
		InOrder_Traverse(T, T->data[index].lchild);
		printf("%3d", T->data[index].weight);
		InOrder_Traverse(T, T->data[index].rchild);
	}
}
 
void PostOrder_Traverse(HuffmanTree * T, int index)
{
	if(index != -1)
	{
		PostOrder_Traverse(T, T->data[index].lchild);
		PostOrder_Traverse(T, T->data[index].rchild);
		printf("%3d", T->data[index].weight);
	}
}

void Level_Traverse(HuffmanTree * T, int index)
{
	int i,j;
	int Queue[QueueSize];
	int front=0,rear=0;
	
	if(index != -1) 
		printf("%3d",T->data[index].weight);	//	先遍历输出根结点（第一层结点） 
 	Queue[rear++] = index;						//	根结点入队，遍历它的左、右孩子 
	while(front != rear)
	{
		int index = Queue[front++];				//	将结点出队，遍历结点的左、右孩子 
		
		if(T->data[index].lchild != -1)
		{
			i = T->data[index].lchild; 
			printf("%3d", T->data[i].weight);
		}
		Queue[rear++] = i;						//	输出该结点后便将其入队，用以访问下一层它的左、右孩子 
		
		if(T->data[index].rchild != -1)
		{
			j = T->data[index].rchild; 
			printf("%3d", T->data[j].weight);
		
		}
		Queue[rear++] = j;						//	输出该结点后便将其入队，用以访问下一层它的左、右孩子 
	}
	
	return ; 
} 

bool Destroy_HuffmanTree(HuffmanTree * T)
{	
	T->n = 0;
	return true;
}