如何判断点是否在凸包内部

例题

https://vjudge.net/problem/UVALive-7281
直接上例题，稍稍梳理一下，如下图

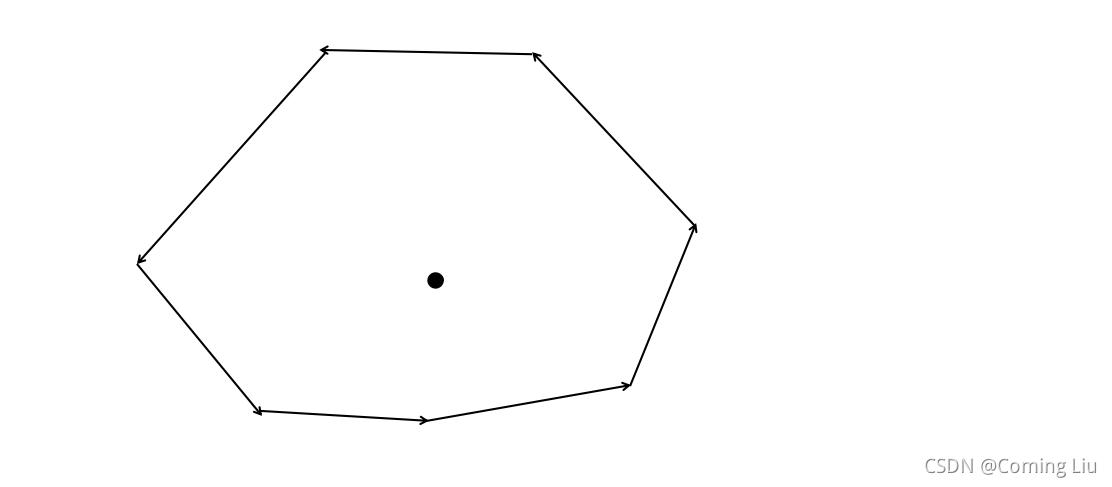
• 思考一下，最简单的办法，按照$Andrew$求凸包的思路，从凸包的某个点沿着逆时针顺序行进，同时看这个点是不是在这条线段左侧，如果到某条线段发现点在这条线段右侧，那么说明这个点就在凸包外侧，判断点在线段的哪一侧使用叉积即可
• 这样的判断时间复杂度是$O(n)$的，对于大规模询问显然不行
• 我们有更好的办法，我们在凸包上进行二分，看下面的图
  
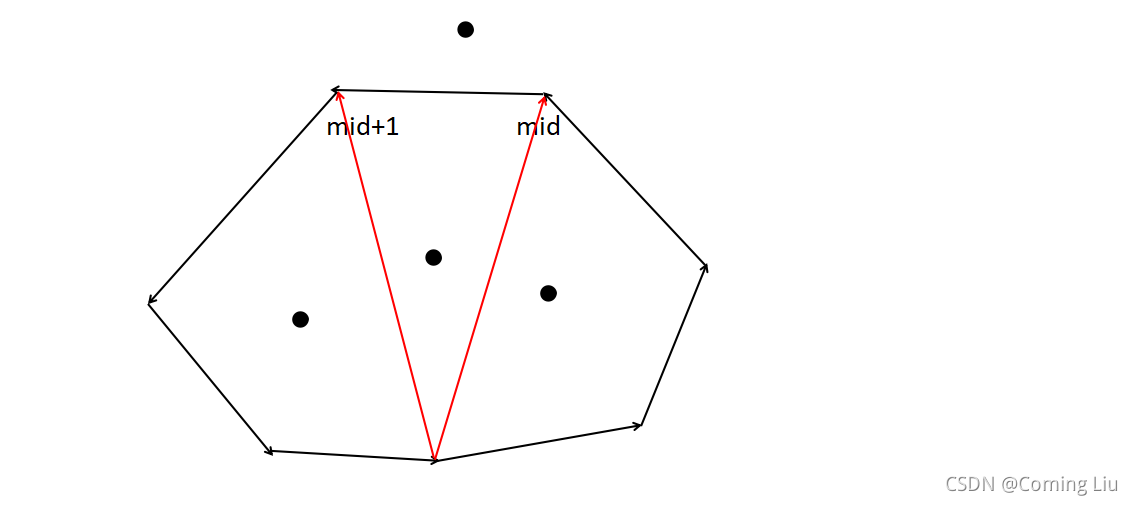
• 这个点的位置只有四种情况（边界一样），在外侧的两种情况可以通过叉积来判断，这是非法情况，内侧的情况可能是合法情况，只需要判断一下这个点是不是在上面的线内部即可，使用叉积判断，比较简单就不细说了，做一下上面的那道题，整理一下模板

#include <bits/stdc++.h>

using namespace std;
#define db double
const db eps = 1e-10;
const int MAXN = 1e4 + 100;
int sgn(db x){
    
    
    if(fabs(x) < eps) return 0;
    return x < 0 ? -1 : 1;
}
struct Point{
    
    
    db x, y;
    Point(){
    
    }
    Point(db x, db y): x(x), y(y){
    
    }
    Point operator + (const Point &B)const{
    
    
        return Point(x + B.x, y + B.y);
    }
    Point operator - (const Point &B)const{
    
    
        return Point(x - B.x, y - B.y);
    }
    bool operator < (const Point &B)const{
    
    
        return sgn(x - B.x) < 0 || (sgn(x - B.x) == 0 && sgn(y - B.y) < 0);
    }
    bool operator == (const Point &B)const{
    
    
        return sgn(x - B.x) == 0 && sgn(y - B.y) == 0;
    }
}s[MAXN], ch[MAXN];
typedef Point Vector;
db Cross(Vector A, Vector B){
    
    
    return A.x * B.y - A.y * B.x;
}
int Convex_hull(int n){
    
    
    int v = 0;
    for(int i=0;i<n;i++){
    
    
        while(v > 1 && sgn(Cross(ch[v - 1] - ch[v - 2], s[i] - ch[v - 2])) <= 0){
    
    
            v -= 1;
        }
        ch[v++] = s[i];
    }
    int j = v;
    for(int i=n-2;i>=0;i--){
    
    
        while(v > j && sgn(Cross(ch[v - 1] - ch[v - 2], s[i] - ch[v - 2])) <= 0){
    
    
            v -= 1;
        }
        ch[v++] = s[i];
    }
    if(n > 1) v -= 1;
    return v;
}
bool check(Point A, int n){
    
    
    int l = 1;
    int r = n - 1;
    while(r - l > 1){
    
    
        int mid = ((r - l) >> 1) + l;
        db a1 = Cross(ch[mid] - ch[0], A - ch[0]);
        db a2 = Cross(ch[mid + 1] - ch[0], A - ch[0]);
        if(sgn(a1) >= 0 && sgn(a2) <= 0){
    
    
            if(sgn(Cross(ch[mid + 1] - ch[mid], A - ch[mid])) >= 0) return true;
            return false;
        }else if(sgn(a1) < 0){
    
    
            r = mid;
        }else{
    
    
            l = mid;
        }
    }
    return false;
}
int main(){
    
    
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int n, m;
    db x, y;
    while(cin >> n){
    
    
        for(int i=0;i<n;i++){
    
    
            cin >> s[i].x >> s[i].y;
        }sort(s, s + n);
        n = unique(s, s + n) - s;
        int len = Convex_hull(n);
        cin >> m;
        int ans = 0;
        for(int i=0;i<m;i++){
    
    
            cin >> x >> y;
            if(check(Point(x, y), len)) ans += 1;
        }
        cout << ans << '\n';
    }
    return 0;
}