机器学习----从线性回归到逻辑斯特回归

原Blog：http://blog.csdn.net/zx10212029/article/details/49889319

Linear Regression

在学习李航《统计学习方法》的逻辑斯特回归时，正好coursera上相应的线性回归和逻辑斯特回归都学习完成，在此就一起进行总结，其中图片多来自coursera课程上。 
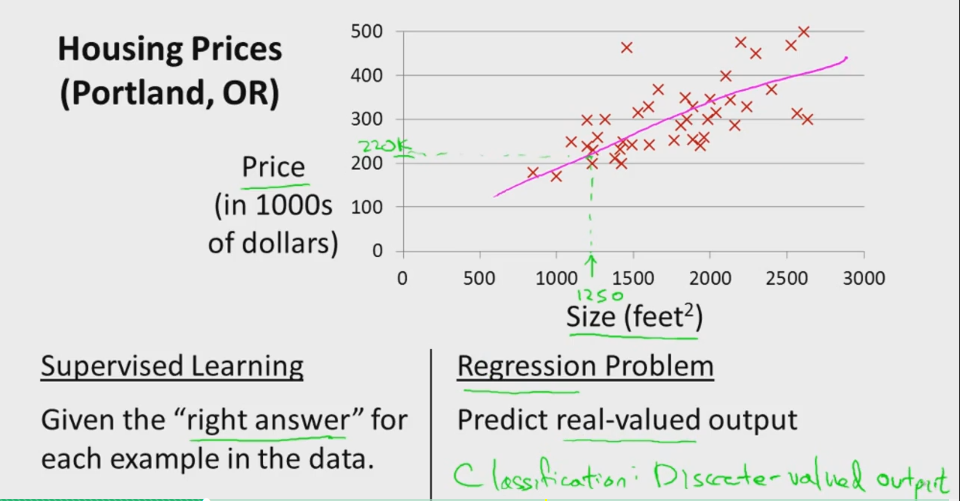
线性回归是机器学习中很好理解的一种算法。我们以常见的房屋销售为例来进行简单分析： 
假设我们统计的一个房屋销售的数据如下： 

在此，我们从单一变量谈起，直观上比较容易理解。训练集定义为 { (x(1),y(1)),(x(2),y(2)),…,(x(m),y(m))} ,其中 x  是输入特征， y  是输出目标， m  是样本的总数目。线性回归的最终目的如下所示，就是通过学习，得到一个拟合函数，使得通过输入特征就能预测目标输出值，本例即通过房屋大小估计房屋价格。 

假设空间

实际线性回归假设能够拟合各种不同的曲线，实际的房子价格可能与房间面积、房间厅室、房间朝向等多个变量有关，我们可以定义特征 x={ x1,x2,…,xi} 那么我们可以定义拟合函数为: 

h(x)=hθ(x)=θ0+θ1x1+θ2x2+…+θixi=θTx

其中  θT=[θ0,θ1,…,θi],xT=[x1,x2,…,xi] ,最后是其向量表达形式。我们可以看出，每一组 θ 值对应一个拟合函数，为了选出其中最好的 θ ，我们定义一个评价标准，即损失函数(loss function)或代价函数(cost function)。

代价函数

在线性回归中，我们定义代价函数为： 

J(θ)=1m∑i=1m12(hθ(x(i))−y(i))2

minθJθ

其中，系数 12 是为了求导方便， 1m 在不同的讲义中可能会有所不同，我们以斯坦福的讲义为标准。 
从表达式我们可以看出，学习的最终目的就是优化代价函数，使代价函数变小了，预测值和真值的差异就越小，训练出来的模型就越好。如何求解 J(θ) 有很多种办法，常见的有梯度下降法和最小二乘法。

梯度下降法

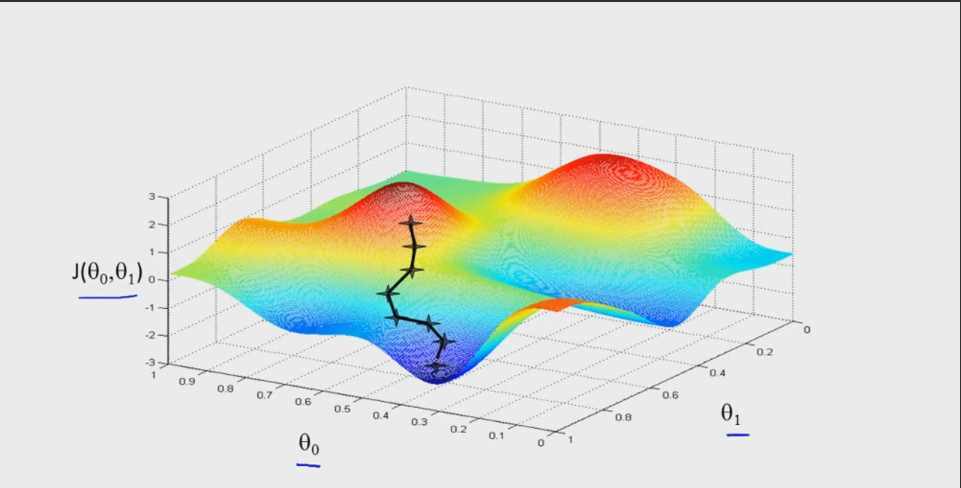
梯度下降法是求解无约束最优化问题的一种最常见的方法，其实现简单，易于理解。如下图所述带有二元参数的目标函数 J(θ0,θ1) ,求解其最小值。我们可以初始化一个参数值 (θ0,θ1) ,然后求 J(θ0,θ1) 在各个方向的偏导，通过一个学习步长来改变参数，并最终求得 J(θ0,θ1) 的最小值。具体算法流程为：

• Algorithm 6.1
• initialize  θ ， θ={ 0,0,…,0}
• for k = 1 : NumIter do
•      θj=θj−α∂∂θjJ(θ)

• end for 
  在线性线性回归中: 
  

  ∂∂θjJ(θ)=1m∑i=1m(hθ(x(i))−y(i))xij
  
  其中 xij 是第 i 个样本实例的第 j 维特征。由此我们就可以学习出每个特征的参数。 
  
  在梯度下降法中有两个个关键参数选择：学习率 α 和初始化 θ 。

• 对于合适的学习率 α ，目标函数  J(θ) 在每次迭代中都会减小，因此可以通过 J(θ) 的值检测算法的正确性。在实际操作中， α 太小，算法的收敛速度会很慢，当 α 太大时，则会出现震荡，学习不到最佳参数。

• 对于初始参数 θ ，不同的起点，可能会得到不同的最优解，即陷入局部最优。

最小二乘法

梯度下降法需要不断的迭代计算，一般来说，收敛速度都会比较慢，另一种快速求解最佳解的方法是最小二乘法，具体公式为： 

θ=(XTX)−1XTY

在自我编程实现中，矩阵逆的求解是一个难点。另外，也存在不可解的情况：一是特征相互关联，不独立；二是样本数少于特征数，可能使得矩阵的逆不存在。

扫描二维码关注公众号，回复： 13301126 查看本文章

过拟合和正则化

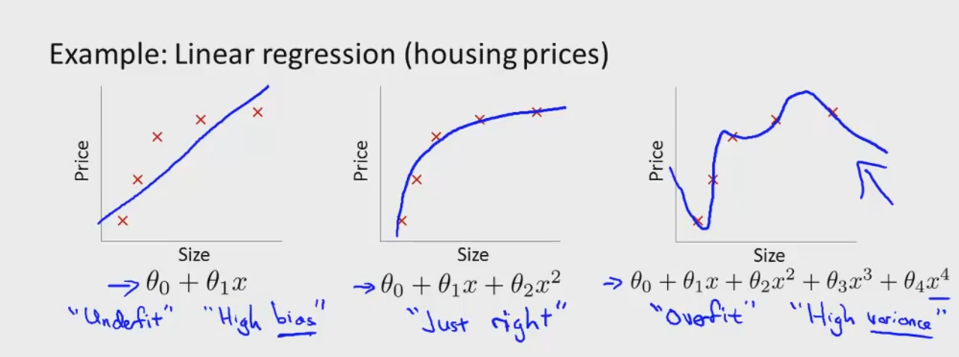
过拟合是机器学习中很普遍的例子，指的是训练模型在训练集上有很好的分类回归效果，但是在新的测试数据集上表现却很差，即模型的泛化能力差。 
如下图所示，依旧以“大小-房价”线性回归为例来说明。房价与房屋大小可能是非线性关系，如图1所示，假设模型为 θ0+θ1x ,即线性关系，拟合效果不好，称为欠拟合；图2则是非线性拟合，假设模型为 θ0+θ1x+θ2x2 ,能够比较好的拟合两者之间的关系；图3所示的多项式 θ0+θ1x+θ2x2+θ3x3+θ4x4 则能够拟合所有的数据，即对训练样本的学习效果很好，但是这明显不是我们所期望的学习模型，存在严重过拟合。 

解决过拟合问题常有以下几种方式：

• 减少特征数量 
     - 人为选择特征，去掉不必要的特征 
     - 机器学习选择特征，主成分分析降维等

• 正则化 
     - 保持所有特征，但是减小学习参数 θ 的值。 
  如上图3所示，通过惩罚项使最终的学习参数 θ3,θ4 极小，则最终模型与图2模型很相近。即： 
  

  min1m{ ∑i=1m(hθ(x(i))−y(i))+1000θ23+1000θ24}
  
  通过将 θ3,θ4 带入到损失函数中，使函数考虑模型复杂度的影响。正则化的目的就是将模型的复杂度考虑到代价函数中，使模型趋于简单，不易过拟合。对于线性回归，正则化代价函数为: 
  
  J(θ)=12m[∑i=1m(hθ(x(i))−y(i))2+λ∑i=1nθ2j]
  
  其中，前面一部分是对训练数据集的拟合误差，后一部分正则化项是对模型复杂度的约束， λ 是调节两则之间的权重：

• 当 λ 较小时，极限情况下 λ=0 ，则不考虑模型的复杂度，是原有的损失函数

• 当 λ 较大时，则训练的参数很小，模型可能会欠拟合

Logistic Regression

回归问题一般是连续预测：如房价预测、销售额预测，即输出 y 的状态可能有无限多种； 
分类问题则是离散预测：邮件分类(垃圾/正常)，细胞检测(正常/癌变)，输出一般对应有限状态。 
一般来说，线性回归不能直接用于分类问题，因为回归是连续性模型，而且受噪音比较大，我们一般选择logistic回归来进行分类。logistic本质是线性回归，只是在特征到结果的映射中加入了一层映射函数。

逻辑斯特回归模型

对于二分类系统，我们希望学习模型的输出为0或1，对于固定的特征，我们希望学习模型预测其属于正例的概率。即： hθ(x)=P(y=1|x:θ) ,对于二分类系统， P(y=1|x:θ)+P(y=0|x:θ)=1 。logistic的假设函数为： 

hθ(x)=g(θTx)=11+e−θTx

如下图所示，我们定义逻辑斯特回归的学习规则为：

• θTx≥0 ,则 hθ(x)≥0.5 ,此时认为样本属于正样本的概率更大，即 y=1
• θTx<0 ,则 hθ(x)<0.5 ,此时认为样本属于正样本的概率更大，即 y=0  
  

决策边界

对于分类问题，最终就是得到一个分类边界，使样本能够被准确区分开。如下图所示的两类样本，我们假设红色为正样本，即 y=1 ,蓝色为负样本，即 y=0 。分类决策面有两个特征 x1,x2 ，因此我们定义假设模型为： hθ(x)=g(θ0+θ1x1+θ2x2) 。取 θT=[−3,1,1] ,即分类平面为 −3+x1+x2=0 ,我们可以看到：

• 当 −3+x1+x2≥0 时，即 θTx≥0 ，此时有 hθ(x)≥0.5 ，决策为正样本，从图中我们可以看到 −3+x1+x2=0 右上侧为正样本
• 同理，当 −3+x1+x2<0 时，即 θTx<0 有 hθ(x)<0.5 ，决策为负样本。 
  通过该直线我们可以将二分类样本正确区分开，这样的边界也称为决策边界。如果样本是非线性可分的，我们也可以通过复杂多项式进行分类。逻辑斯特回归最终学习到的模型就是这样的边界图，在边界的两边就是两个不同的类别。 
  

损失函数

逻辑斯特回归代价函数一般定义为： 

Cost(hθ(x),y)={ −log(hθ(x)),−log(1−hθ(x)),if y=1if y=0

因为 hθ(x) 是输出为(0,1)之间的函数，如果真值为 y=1 ，预测值 hθ(x) 越接近1，代价越小，即预测越正确。同理，真值为 y=0 ，预测值 hθ(x) 越接近0，代价越小，即预测越正确。我们可以将代价函数改写为： 

Cost(hθ(x),y)=−ylog(hθ(x))−(1−y)log(1−hθ(x))

最终的代价函数为： 

J(θ)=−1m∑i=1m[y(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i)))]

如果考虑模型的复杂度，即加入正则项，则为： 

J(θ)=−1m∑i=1m[y(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i)))]+12m∑j=1nθ2j

最终目标是最小化目标函数，用梯度下降法求解，则： 

∂∂θjJ(θ)=−1m∑i=1m[y(i)1hθ(x(i))h′θ(x(i))−(1−y(i))11−hθ(x(i))h′θ(x(i))]=−1m∑i=1m[y(i)−y(i)hθ(x(i))−hθ(x(i))+y(i)hθ(x(i))hθ(x(i))(1−hθ(x(i)))]h′θ(x(i))=−1m∑i=1m[y(i)−hθ(x(i))11+e−θTxe−θTx1+e−θTx]e−θTx(1+e−θTx)2x(i)j=1m∑i=1m(hθ(x(i))−y(i))x(i)j

通过推导我们发现逻辑斯特回归的代价函数与线性回归形式上很像，不同之处在于模型假设不一样，线性回归是 hθ(x)=θTx ， 而逻辑回归在此基础上多了一层映射 hθ(x)=11+e−θTx

多分类问题

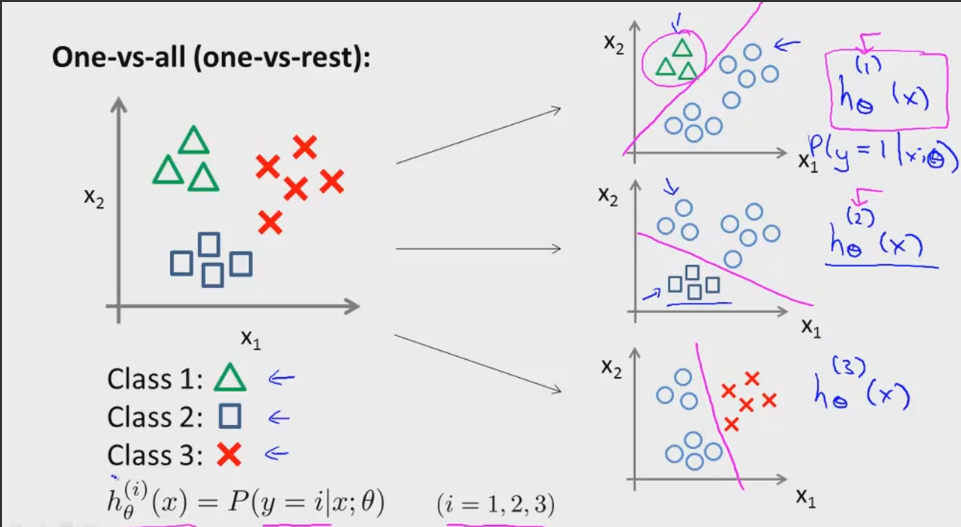
logistic回归也可用于扩展用于多分类问题，解决办法常见的就是一对多。如下图所示有三类样本，我们可以先用一个分类器将类别一与另外两类区分开(右图1)，然后用同样的办法训练两个分类器，将每个类别区分开。在得到的三个假设模型中，我们计算每个样本在每个模型中的值，即概率，通过选取最大的概率，就能确定样本所属的类别。 

Python实现

最后我们通过Python实现了简单的logistic二分类问题，具体代码如下： 
读取txt文件中的训练数据，包含特征和标签，并给特征加上偏置项1

# load training data set
def loadData(path):
    dataMat = []; labelMat = [];
    f = open(path)
    data= f.read().split()
    for datastring in data:
        dataMat.append([1,float(datastring.split(',')[0]),float(datastring.split(',')[1])])
        labelMat.append(int(datastring.split(',')[2]))
    return dataMat,labelMat
 
  
  

   
   
1
   
   
2
   
   
3
   
   
4
   
   
5
   
   
6
   
   
7
   
   
8
   
   
9
  
  

从txt中读取的特征值很大，进行标准归一化之后进行训练。

def featureNormalize(dataMat):
    dataMatrix = mat(dataMat)
    data_norm = dataMatrix;
    m,n = shape(dataMatrix)
    mu = mean(dataMatrix[:,1:3],axis = 0)
    sigma = std(dataMatrix[:,1:3],axis = 0)
    data_norm[:,1:3]= [x/y for x,y in zip((dataMatrix[:,1:3]-tile(mu,(m,1))),tile(sigma,(m,1)))]
    return data_norm,mu,sigma
 
  
  

   
   
1
   
   
2
   
   
3
   
   
4
   
   
5
   
   
6
   
   
7
   
   
8
  
  

绘制最终分类效果图和损失函数的变化

# plot data set
def plotdata(theta,mu,sigma,dataMat,labelMat):
    dataArr = array(dataMat)
    positive_x =[]; positive_y = []
    negtive_x =[]; negative_y = []
    for i in range(len(labelMat)):
        if 1 == int(labelMat[i]):
            positive_x.append(dataArr[i,1]);positive_y.append(dataArr[i,2])
        else:
            negtive_x.append(dataArr[i,1]);negative_y.append(dataArr[i,2])
    fig1 = plt.figure('fig1')
    ax = fig1.add_subplot(111)
    ax.scatter(positive_x,positive_y,s=30,c='red',marker='s')
    ax.scatter(negtive_x,negative_y,s=30,c='green')
    min_x = min(dataArr[:,1])
    max_x = max(dataArr[:,1])
    y_min_x = (-theta[0]-theta[1]*(min_x-mu[0,0])/sigma[0,0])*sigma[0,1]/theta[2]+mu[0,1]
    y_max_x = (-theta[0]-theta[1]*(max_x-mu[0,0])/sigma[0,0])*sigma[0,1]/theta[2]+mu[0,1]
    ax.plot([min_x,max_x],[y_min_x,y_max_x],'-g')
    plt.xlabel('X1');plt.ylabel('X2');plt.legend();
    plt.show()

# plot cost
def plotJ(J_history):
    fig2 = plt.figure('fig2')
    ax = fig2.add_subplot(111)
    x = arange(0,len(J_history),1)
    ax.plot(x,J_history)
    plt.xlabel('Iter');plt.ylabel('cost');plt.legend();
    plt.show()
 
  
  

   
   
1
   
   
2
   
   
3
   
   
4
   
   
5
   
   
6
   
   
7
   
   
8
   
   
9
   
   
10
   
   
11
   
   
12
   
   
13
   
   
14
   
   
15
   
   
16
   
   
17
   
   
18
   
   
19
   
   
20
   
   
21
   
   
22
   
   
23
   
   
24
   
   
25
   
   
26
   
   
27
   
   
28
   
   
29
   
   
30
  
  

梯度下降算法：

# sigmoid function
def sigmoid(z):
    return 1.0 / (1+exp(-z))

# train 
def gradientReg(dataMat,labelMat,alpha,lambda1,MaxIter):
    dataMatrix = mat(dataMat)
    labelMatrix = mat(labelMat).transpose()
    m,n = shape(dataMatrix)
    J = zeros((MaxIter,1))
    theta = zeros((n,1))
    for k in range(MaxIter):
        h = sigmoid(dataMatrix*theta)
        J[k] = 1.0/m*sum(-multiply(labelMatrix,log(h))-multiply((1-labelMatrix),log(1-h)))+\
        lambda1/(2*m)*(sum(theta[2:n]**2))
        error = (h-labelMatrix)
        for i in range(n):
            if 0 == i:
                theta[i] = theta[i] - alpha*1.0/m*(error.transpose()*dataMatrix[:,i])
            else:
                theta[i] = theta[i] - alpha*1.0/m*(error.transpose()*dataMatrix[:,i]+lambda1*theta[i]) 
    return theta,J  
 
  
  

   
   
1
   
   
2
   
   
3
   
   
4
   
   
5
   
   
6
   
   
7
   
   
8
   
   
9
   
   
10
   
   
11
   
   
12
   
   
13
   
   
14
   
   
15
   
   
16
   
   
17
   
   
18
   
   
19
   
   
20
   
   
21
   
   
22
  
  

通过训练模型进行分类预测

# predict 
def predict(theta,dataMat):
    prob = sigmoid(dataMat*theta)
    p = double(prob>0.5)
    return p;
 
  
  

   
   
1
   
   
2
   
   
3
   
   
4
   
   
5
  
  

主函数

# main
if __name__=="__main__":
    dataMat = []; labelMat = [];
    alpha = 0.1;lambda1 = 0; MaxIter = 1000;
    datapath = 'F:\Program\Python\Machine_Learning\Logistic\src\ex2data1.txt'
    dataMat,labelMat=loadData(datapath)
    data_norm,mu,sigma =featureNormalize(dataMat)
    theta,J_history = gradientReg(data_norm,labelMat,alpha,lambda1,MaxIter)
    plotdata(theta,mu,sigma,dataMat,labelMat)
    plotJ(J_history)
    p = predict(theta,data_norm)
    print "the classify accuracy is:%.3f%%" %(mean(double(p.transpose() == labelMat)) * 100)
 
  
  

   
   
1
   
   
2
   
   
3
   
   
4
   
   
5
   
   
6
   
   
7
   
   
8
   
   
9
   
   
10
   
   
11
   
   
12
  
  

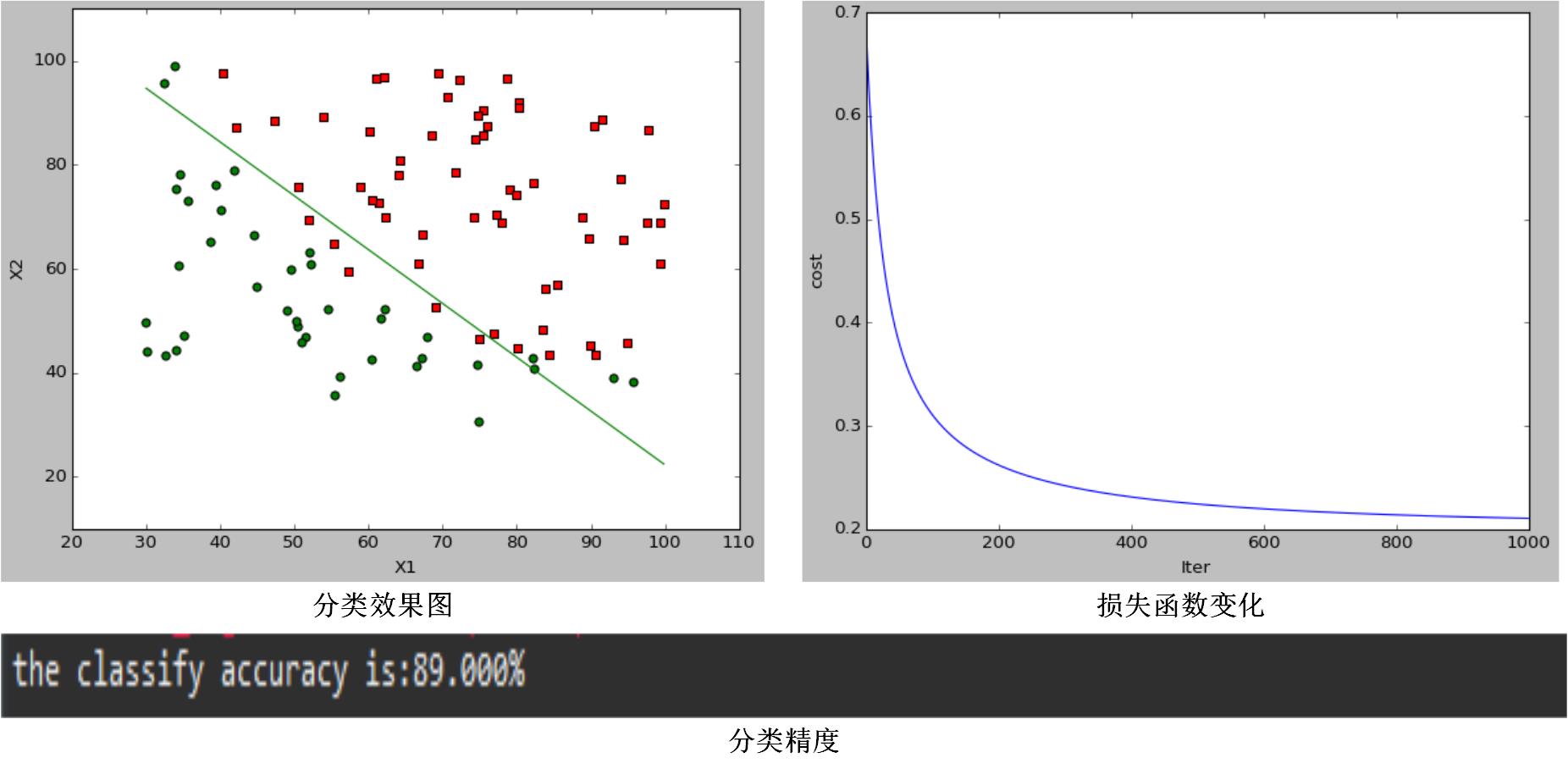
当 α=0.1,λ=0 时，分类效果图为： 

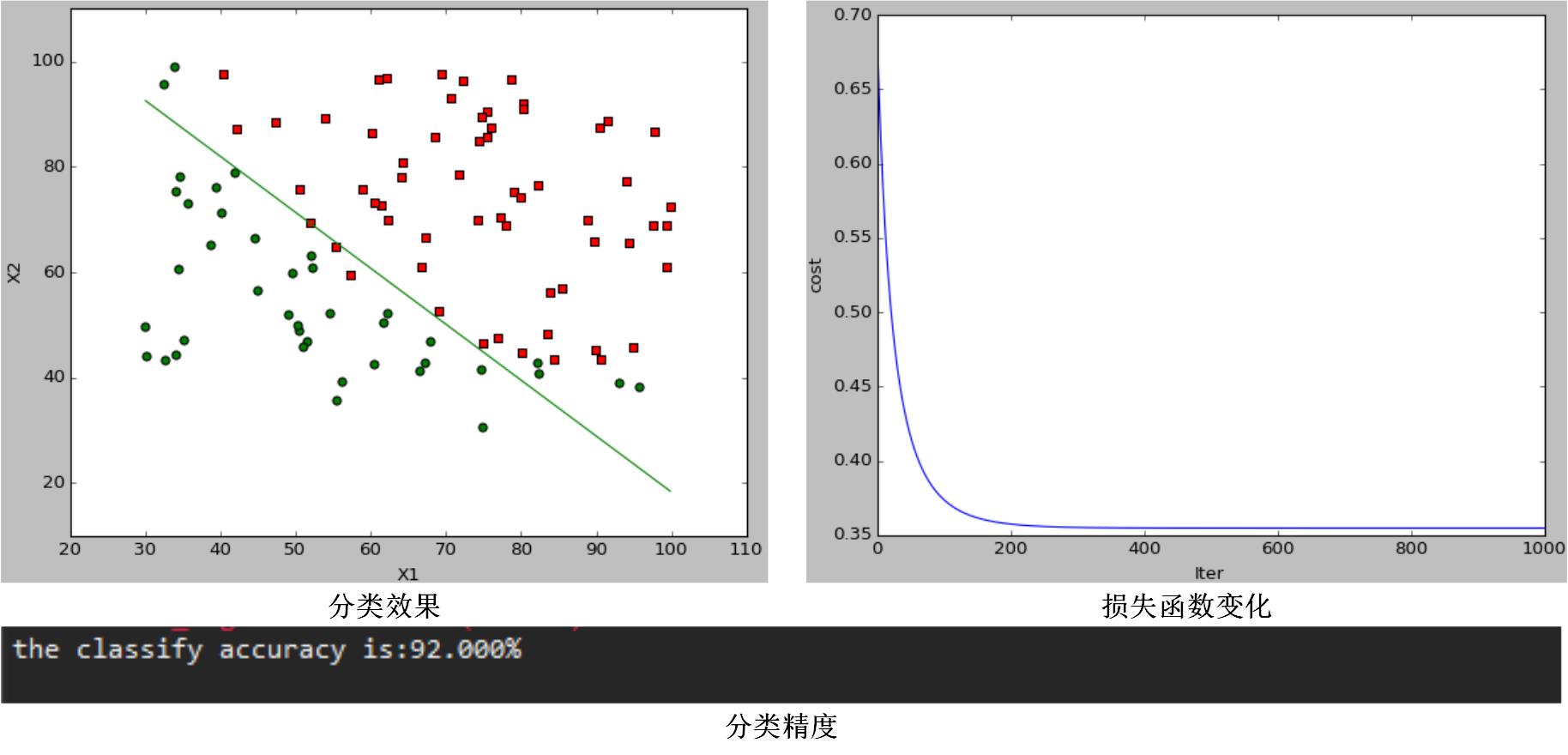
当 α=0.1,λ=10 时，分类效果图为： 

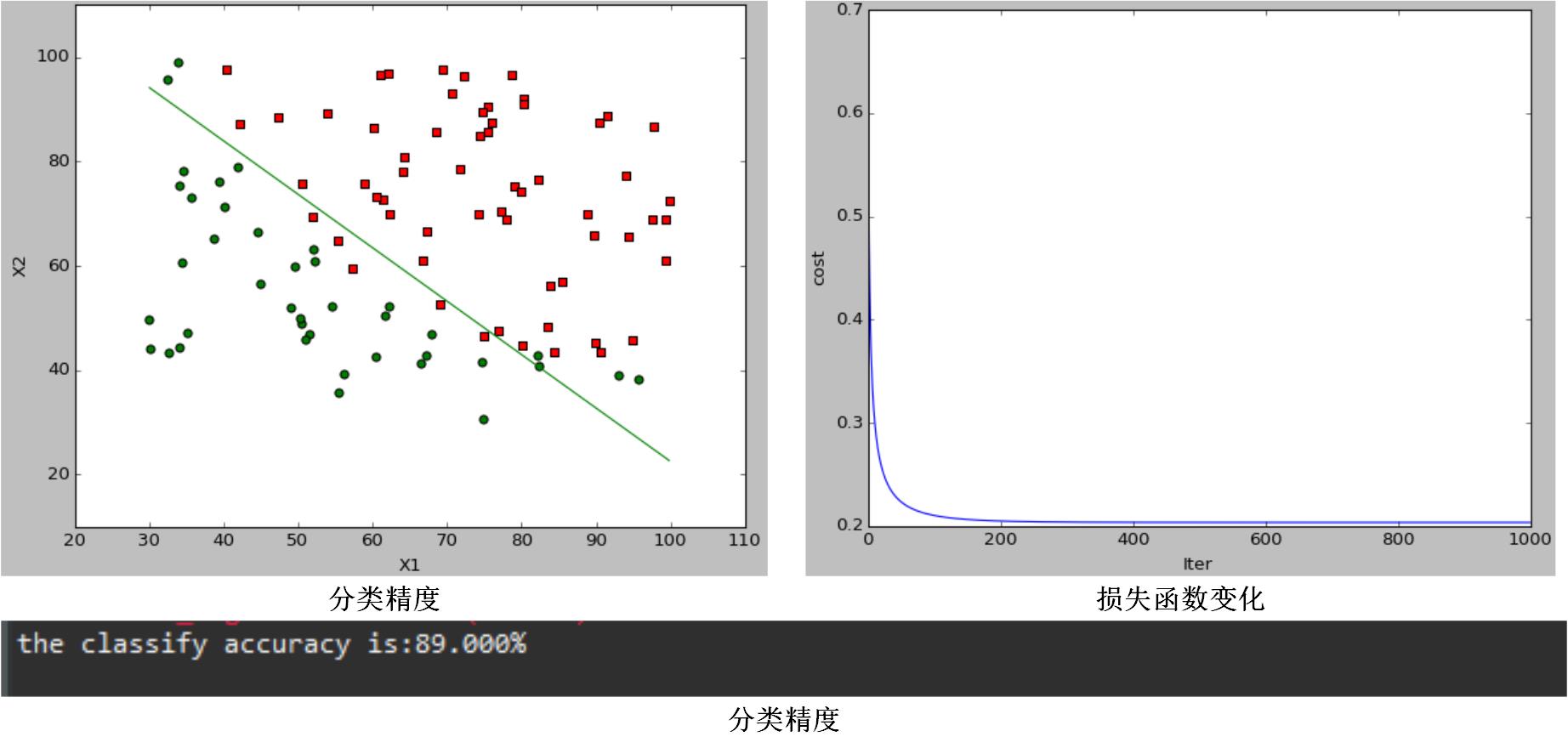
当 α=1,λ=0 时，分类效果图为： 

通过对比图1和图2，可以发现当调节参数 λ 变化时，代价函数会改变，分类效果和分类结果都会变化，说明它通过引入正则项可以改变模型的复杂程度；通过对比图1和图3，可以发现，在一定范围内 α 越大，代价函数收敛越快，模型学习迭代次数越少，但是模型最终分类效果和分类结果都没变化，学习率只影响了模型训练速度，而不会影响模型的性能。