卷积神经网络(Convolutional Neural Network, CNN)是一种前馈神经网络,和普通神经网络相似,都是由具有可学习权重和偏差的神经元组成。那有什么区别,ConvNet架构明确假设输入是图像,这允许我们将某些属性编码到架构中。然后,这些使得前向功能更有效地实现并且大大减少了网络中的参数量。
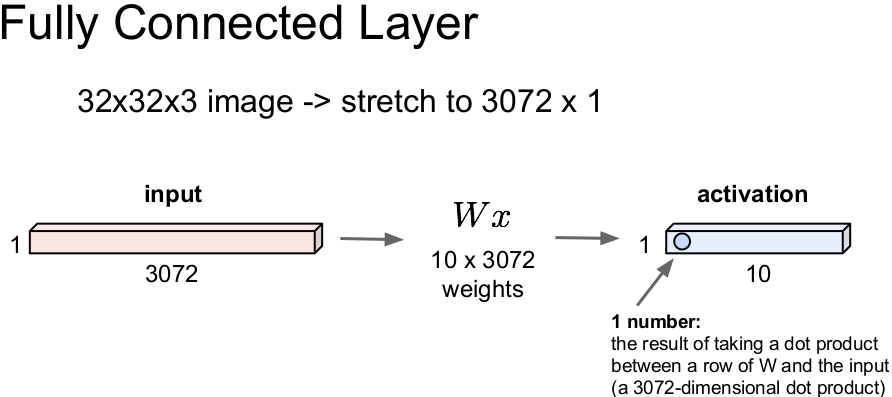
常规神经网络采用完全连接结构,对于 32*32*3 的图像会先“拍平”成 3072*1 再进行运算,而卷积神经网络利用输入由图像组成的事实,依然保留着原来的空间结构。
|
|
|
构建ConvNets的主要层包括卷积层,池化层和完全连接层。
卷积层 Convolutional Layer
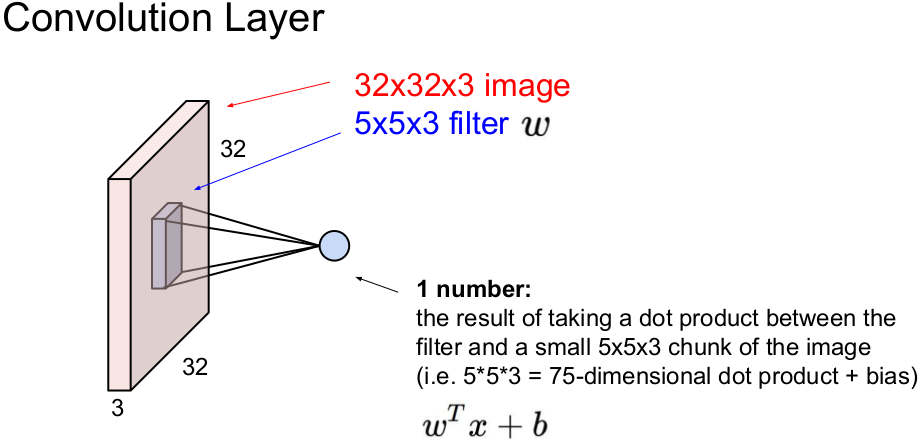
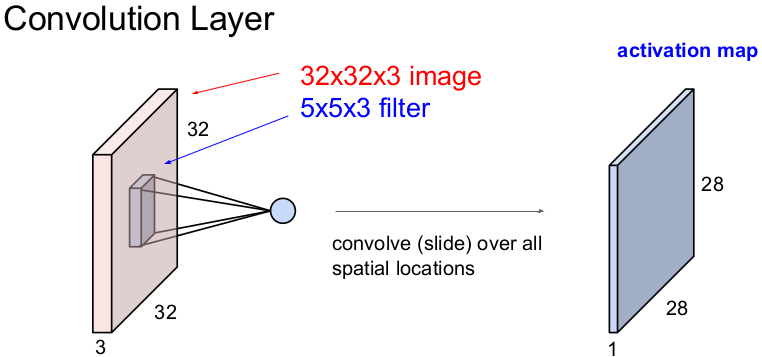
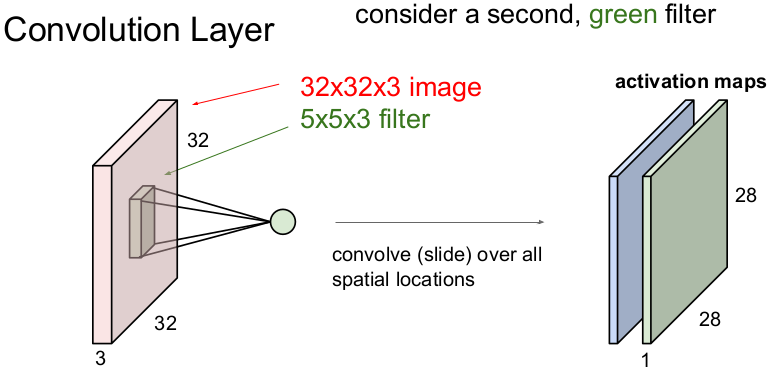
Conv层是卷积网络的核心构建块,Conv层的参数由一组可学习的过滤器组成。在前向传递过程中,我们在输入体积的宽度和高度上滑动(更准确地说,卷积)每个滤波器,并计算滤波器条目和任何位置输入之间的点积,将生成一个二维激活图,该图在每个空间位置给出该滤波器的响应,沿深度维度堆叠这些激活图并生成输出量。
|
|
|
那卷积过程到底如何操作的,几个参数了解下:
- 深度 depth : 神经元个数,也决定了输出的 depth ,也代表滤波器个数
- 步长 stride : 滤波器滑动间距
- 补零 zero-padding : 在输入体外围补0来控制输出体积空间大小(不是必须的),如右下图
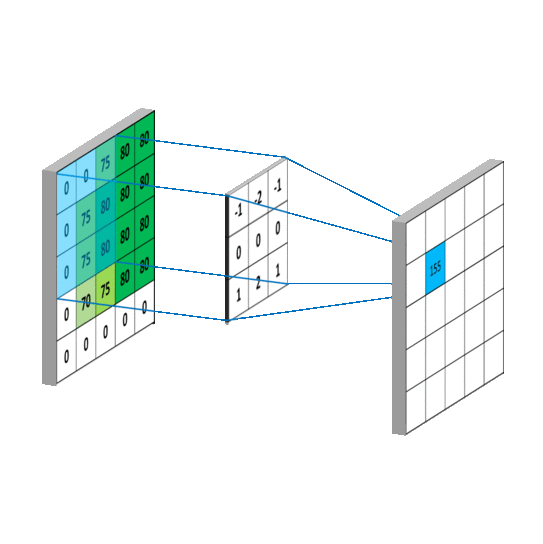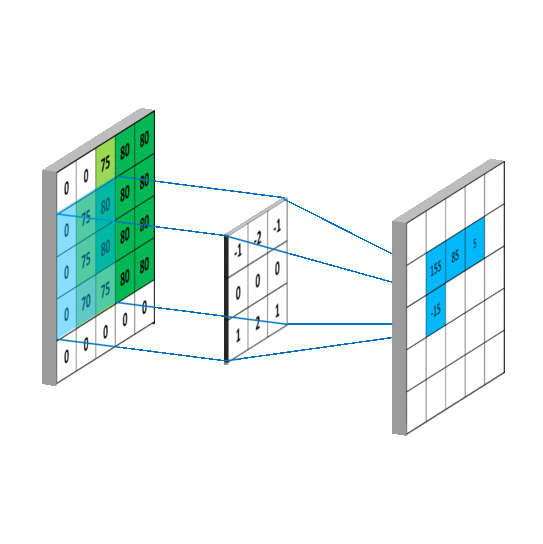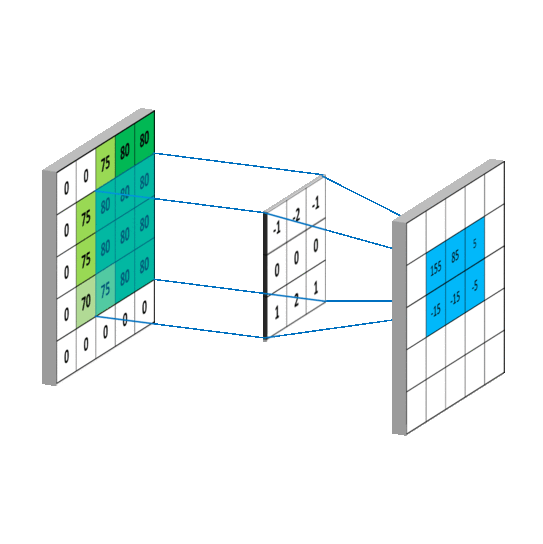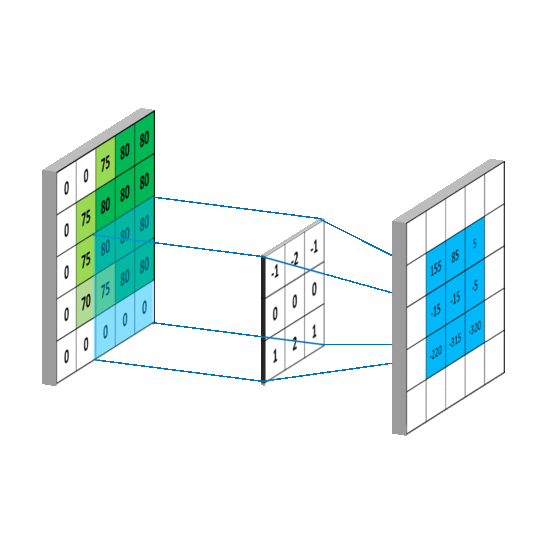
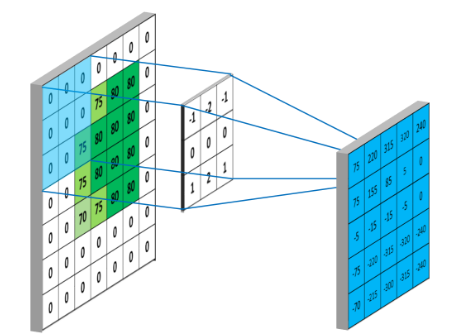
下图左边显示了输入5x5,步长为1,深度为1,未补0时的卷积计算过程。所谓卷积,通俗来讲,在离散空间为加权求和,以第一个计算结果155为例:
0 x (-1) + 0 x (-2) + 75 x (-1) + 0 x 0+ 75 x 0+ 80 x 0+ 0 x 1+ 75 x 2+ 80 x 1 = 155
|
|
|
对于输出的空间大小有如下描述:
给定输入体积size W,感知野大小(滤波器size)F,步长S,补零数P,那么输出为 。
eg. 输入体积为 32 x 32 x 3 ,10个5x5滤波器,步长1,补零为2,则输出体积大小为 (32 + 2*2 -5)/1 + 1 = 32,即 32 x 32 x 10,该层的参数个数为 (5*5*3 + 1)*10 = 760.
|-------- 每个滤波器参数 (+1是因为偏置量)
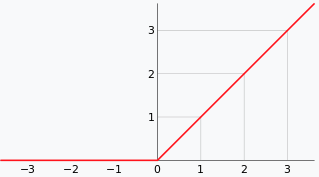
线性整流层 Rectified Linear Units layer, ReLU layer



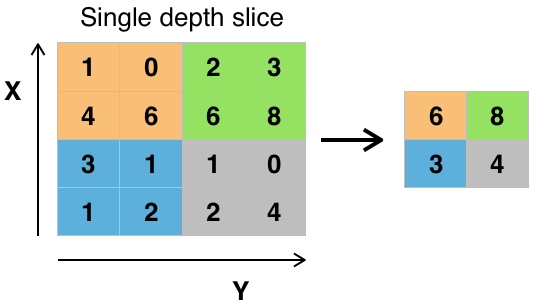
池化层 Pooling Layer
实际上是一种形式的下采样。有多种不同形式的非线性池化函数,而其中“最大池化(Max pooling)”是最为常见的。它是将输入的图像划分为若干个矩形区域,对每个子区域输出最大值。池化层会不断地减小数据的空间大小,因此参数的数量和计算量也会下降,这在一定程度上也控制了过拟合。
|
|
|
需要注意的是现在很多人建议丢弃这一层,而是在卷积层使用较大的步长来减少数据空间大小,并且发现这对于训练出好的模型非常重要,例如变分自编码器VAEs,可能在将来架构中,池化层会比较少用。
Summary
- 卷积神经网络是对卷积层,池化层和全连接层的堆叠
- 趋向于更小的滤波器和更深的架构
- 趋向于控制池化层和全连接池(只使用卷积层)
- 经典的架构类似
[(CONV-RELU)*N-POOL?]*M-(FC-RELU)*K,SOFTMAX
where N is usually up to ~5, M is large, 0 <= K <= 2.但是目前比较流行的 ResNet/GoogLeNet
在挑战这种框图
Q:为什么Conv有效
1. 局部相关性。图像的空间联系是局部的像素联系比较密切,而距离较远的像素相关性较弱,因此,每个神经元没必要对全局 图像进行感知,只要对局部进行感知,然后在更高层将局部的信息综合起来得到全局信息。
2. 权值共享,降低了模型参数数量,控制了模型复杂度。基于一个合理的假设:如果一个特征对于在某个空间位置(x,y)计算 是有用的,那么在一个不同位置(x2 ,y2)上计算它也应该是有用的。