4.语法分析
自顶向下(Top Down)【从文法产生语言的角度】(从根开始,逐步为某语句构造一棵语法树):
- 递归子程序法
- 预测分析法(LL(1))
自底向上(Bottom Up)【从自动机识别语言的角度】(相反,将一句子归约为开始符号):
- 算符优先分析法
- LR(0),SLR(1),LR(1),LALR(1)
这些是解决确定性问题的。也就是说每种算法由他的判定条件来决定使用什么文法。
同时假定文法是压缩的:即产生了无用产生式。(如S->ab,A->c,后者是走不到的状态,输入的时候就该删掉了)
4.1自顶向下语法分析
4.1.1基本思想
- 自顶向下语法分析的基本思想
- 从文法的开始符号出发,寻求所给的输入符号串的一个最左推导
- 从树根S开始,构造所给输入符号串的语法树
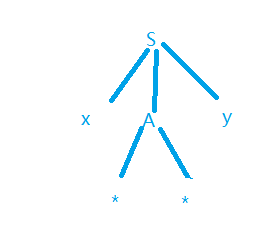
例:设有G: S − > x A y {S->xAy} S−>xAy , A − > ∗ ∗ ∣ ∗ {A->**|* } A−>∗∗∣∗ ,输入串: x ∗ ∗ y {x**y} x∗∗y
S − > x A y − − > {S->xAy-->} S−>xAy−−> x ∗ ∗ y {x**y} x∗∗y
4.1.2二义性问题
- 对于文法G,如果L(G)中存在一个具有两棵或两颗以上分析树的句子,则称G是二义性的。也可以等价地说:如果L(G)中存在一个具有两个或两个以上最左(或最右)推导的句子,则G是二义性文法
- 如果一个文法G是二义性的,则 w ∈ L ( G ) {w∈L(G)} w∈L(G)且w存在两个最左推导,则在对w进行自顶向下的语法分析时,语法分析程序无法确定采用w的哪个最左推导。
比如给一个id+id*id。就有两种构造方式。因为没有规定出运算的优先级。如果把优先级定义清楚就可以消除二义性。

4.1.3回溯问题
- 文法中每个语法变量A的产生式右部称为A的候选式,如果A有多个候选式存在公共前缀,则自顶向下的语法分析程序将无法根据当前输入符号准确地选择用于推导的产生式,只能试探。当试探不成功时就需退回到上一步推导,看A是否还有其他的候选式。
- Ge:E->T,E->E+T,E->E-T,T->F,T->T*F,T->T/F,F->(E),F->id
- 例如,考虑为输入串id+id*id建立最左推导
- E = > T {E=>T} E=>T
- E = > T = > F {E=>T=>F} E=>T=>F
- E = > T = > F = > ( E ) {E=>T=>F=>(E)} E=>T=>F=>(E)
- E = > T = > F = > i d {E=>T=>F=>id} E=>T=>F=>id
- E = > T = > T ∗ F {E=>T=>T*F} E=>T=>T∗F
- …
之后将采用提取左因子的方法来改造文法,以便减少推导过程中回溯现象的产生。当然单纯通过提取左因子无法彻底避免回溯现象产生。
4.1.4左递归-无穷推导问题
- 假设A是文法G的某个语法变量,如果存在推导 A = > + α A β {A\stackrel{\mathrm{+}}{=>}αAβ} A=>+αAβ,则称文法G是递归的。当 α \alpha α= ϵ \epsilon ϵ时称之为左递归;如果 A α A β {AαAβ} AαAβ至少需要两步推导,则称文法G是间接递归的,当 α \alpha α= ϵ \epsilon ϵ时称之为间接左递归。如果文法G中存在形如 A = > α A β {A{=>}αAβ} A=>αAβ的产生式,则称文法G是直接递归的,当 α \alpha α= ϵ \epsilon ϵ时称之为直接左递归。
- Ger:E->T,E->E+T, E->E-T,T->T*F,T->T/F,F->(E),F->id
- 考虑为输入串id+id*id建立一个最左推导
- E − > E + T − > E + T + T − > E + T + T − > . . . . {E->E+T->E+T+T->E+T+T->....} E−>E+T−>E+T+T−>E+T+T−>....
- 间接左递归: E − > F + a , F − > E − b {E->F+a},{F->E-b} E−>F+a,F−>E−b
- E = > E − b + a E=>E-b+a E=>E−b+a
4.1.5对上下文无关文法的改造
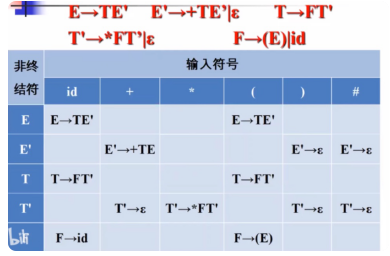
4.1.5.1引入新的文法变量划分优先级
越下面的优先级更高,越上面的优先级越低。

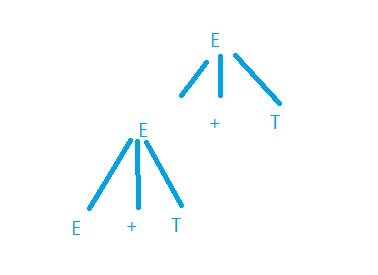
i d + i d ∗ i d {id+id*id} id+id∗id 时对应的是左边的语法树。因为最开始推导的时候这个E只能解释成加法式,减法式子,或者T。若先走T会变成 E = > T = > T ∗ F {E=>T=>T*F} E=>T=>T∗F对于F表示id没有问题,但是对于T表示id+id就是不合理的了。因此规避了加减法和乘除法优先级不对的问题。
扫描二维码关注公众号,回复: 13465021 查看本文章
i d + i d − i d {id+id-id} id+id−id又对应的是什么情况呢?
E=》E+T=》E=》E+T+T
E=》E-T=》E+T-T

4.1.5.2消除左递归(直接和间接)
-
直接左递归的消除(转化为右递归)
-
引入新的变量 A ′ {A'} A′,将左递归产生式 A − > A α ∣ β {A->Aα|β} A−>Aα∣β替换为 A − > β A ’ {A->βA’} A−>βA’, A ′ − > α A ’ ∣ ϵ {A'->αA’|{\epsilon}} A′−>αA’∣ϵ
4.1.5.3提取左因子
消除一步的选择困难

练习:
提取左因子: S − > a A ∣ a B ∣ a C ∣ a ∣ b ∣ c S->aA|aB|aC|a|b|c S−>aA∣aB∣aC∣a∣b∣c
S − > a S ′ ∣ a ∣ b ∣ c {S->aS'|a|b|c} S−>aS′∣a∣b∣c
S ′ − > A ∣ B ∣ C {S'->A|B|C} S′−>A∣B∣C
4.1.6回退式语法分析
什么样的文法对其句子才能进行确定的自顶向下分析
从开始符号(根)往下扩展的途中怎么确定下一步用什么产生式子呢?
最基本的方法就是遍历,试错。错了回溯。
遍历有两种:一种是dfs,一种是bfs。
普遍来说,我们只能来猜。
4.1.6.1bfs

- 语法分析可视为搜索过程。
- 就如上面的int+int,扩展到某一层出现了int+int。因此该树链就是所有的推导过程。

做法:
- 维护一个工作列表,用于存储待处理的句型,初始值只包含开始符号
- While工作列表不为空
- 每次从工作列表取出一个句型,从列表中删除
- 如果弹出的句型与待识别的字符串一样,则成功
- 否则将此句型一步推导的所有句型入队列
分析:
- 最坏情况下是指数级,不管空间和时间
- 而且大多数搜到的状态都是无用的,效率低下

优化:扩展节点时都只看最左边一步推导的状态(最左推导)
- 节点扩展的时候规模变小的,底数变小,总体复杂度不变。只是一定程度提高。
4.1.6.2dfs
同样,我们dfs也考虑最左推导。
dfs的期望复杂度比bfs好。

4.1.6.3bfs与dfs的比较
- BFS parsing
- 适用于任何文法
- 效率低
- DFS parsing
- 无法处理左递归
- 期望O(nlogn),也能到指数级
因此需要人写出不错的文法来达到特定算法的运行效率提高。
由此我们搞出了前瞻式语法分析:如LL(1)
4.1.7前瞻式语法分析
核心思想:利用前瞻字符确定产生式的选择
多数是线性算法
处理文法范围更小(需要文法满足特定条件,也就是用表达能力换取计算效率)
需要预测分析表
4.1.7.1 LL(1)语法分析
LL(1)
第一个L:字串读入方向
第二个L:推导方向为最左推导
(1):往前看1个字符(前瞻字符的个数)
- LL(1)语法分析总程序
- 需要给定LL(1)预测分析表
- 预测分析表构建
- 需要给定FIRST,FOLLOW集合
- FIRST,FOLLOW集合
- 定义、算法

4.1.7.1.1预测分析表匹配
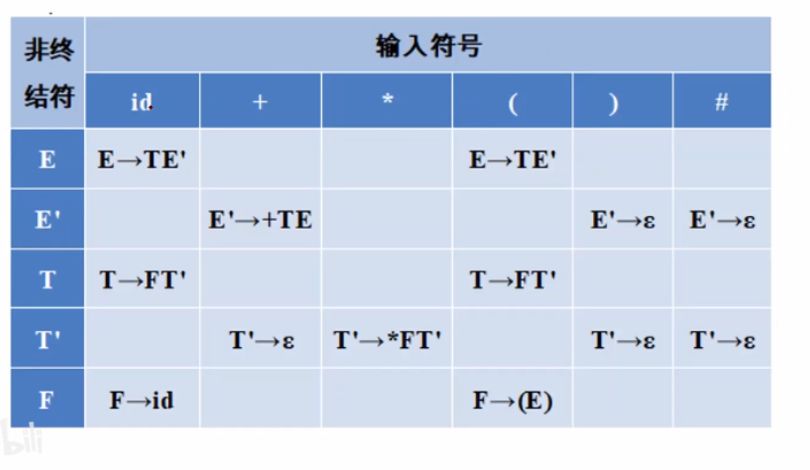
- 非终结符就是行标题
- 列坐标是所有可能出现的终结符
- 如果当前在分析非终结符时往后看了一步发现下一步读入的字符串是列坐标这(比如id),这时候应该用哪个产生式扩展就放在表格里。
- 如果没有写却出现了,报错。 比如分析到E’->id,但是表格里没有

匹配的过程主要有两个:
- Predict Step:
- 前瞻
- 查表选定产生式
- 推导并压栈
- Match Step
- 匹配终结符
- 弹出栈并后移读串光标
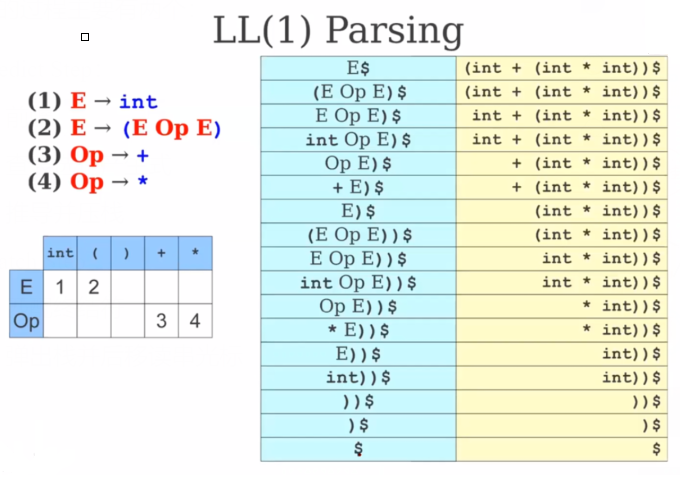
- 把匹配的过程标号写出来就可以构建语法树

练习①:
缓冲区: i d + i d ∗ i d {id+id*id} id+id∗id
练习②:
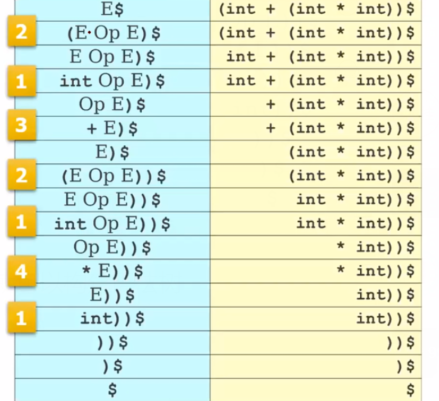
( 1 ) E − > i n t {(1)E->int} (1)E−>int
( 2 ) E − > ( E o p E ) {(2)E->(E op E)} (2)E−>(EopE)
( 3 ) O p − > + {(3)Op->+} (3)Op−>+
( 4 ) O p − > ∗ {(4)Op->*} (4)Op−>∗
缓冲区: ( i n t ( i n t ) ) {(int(int))} (int(int))
做的时候分析结果说明字符串错了,文法不接受这个匹配串。
KaTeX parse error: Expected '}', got 'EOF' at end of input: {OpE)}$ ( i n t ) ) {(int))} (int))
Op匹配不到(。
- 预测分析程序的总控程序
输入:输入串w和文法G=(G,T,P,S)的分析表M
输出:如果w属于 L ( G ) {L(G)} L(G),则报告accpet并输入w的最左推导,否则error
步骤:
- 将结束符号#和文法开始符S压入栈
- 在w末尾添加#,输入指针指向w首字母
- while 栈不空 do
- 记当前栈顶符号为X,当前输入符号为a
- if X=a=# then report accept
- if X∈T∪{#} them //Match step
- if X ≠ a then report error
- else 将弹出栈,并前移输入指针
- else //Predict step
- if M[X,a] 无定义 then report error
- else 记M[X,a] 为X-> Y 1 Y 2 . . . Y k {Y_{1}Y_{2}...Y_{k}} Y1Y2...Yk
- 将X弹出栈,依次将 Y 1 Y 2 . . . Y k {Y_{1}Y_{2}...Y_{k}} Y1Y2...Yk入栈
- 输出产生式:X-> Y 1 Y 2 . . . Y k {Y_{1}Y_{2}...Y_{k}} Y1Y2...Yk
4.1.7.1.2什么是确定的自顶向下分析
栈顶非终结符与输入终结符a决定所用的(唯一)产生式
因此我们给出定义:如果给定一个文法,对于任意给定非终结符E与终结符a,都能唯一地确定产生式(确定的自顶向下语法分析),则称该文法为LL(1)文法。
S − > a A ∣ a B {S->aA|aB} S−>aA∣aB
A − > a {A->a} A−>a
B − > b {B->b} B−>b
上述是否满足LL(1)文法定义。
不能。对于开始非终结符号S,不能决定是aA还是aB。共用了一个终结符前缀。
比如 X − > w 1 ∣ w 2 ∣ . . . ∣ w n {X->w_{1}|w_{2}|...|w_{n}} X−>w1∣w2∣...∣wn ,假如里面存在 w i {w_{i}} wi和 w j {w_{j}} wj存在a为前缀,遇到这种输入就不能唯一确定产生式了。
S − > A ∣ B {S->A|B} S−>A∣B
A − > a a {A->aa} A−>aa
B − > a b {B->ab} B−>ab
假如LL(1)文法,缓冲区为ab的时候,只能看到a,不能保证唯一。进一步推导不能保证唯一前缀。
因此启发我们不能只看一步推导。
比如说下面的式子。
对于非终结符EXPR(5)(6)(7)(8)和TERM都是唯一的,因为没有两个推导存在公共前缀。
对于(4),经过一步推导是可以到id和constant的。
对于(1)和(2)碰到if和while是唯一的。
而(3)遇到的是EXPR,也就是说EXPR可能遇到的他都可能遇到,成为首终结符。
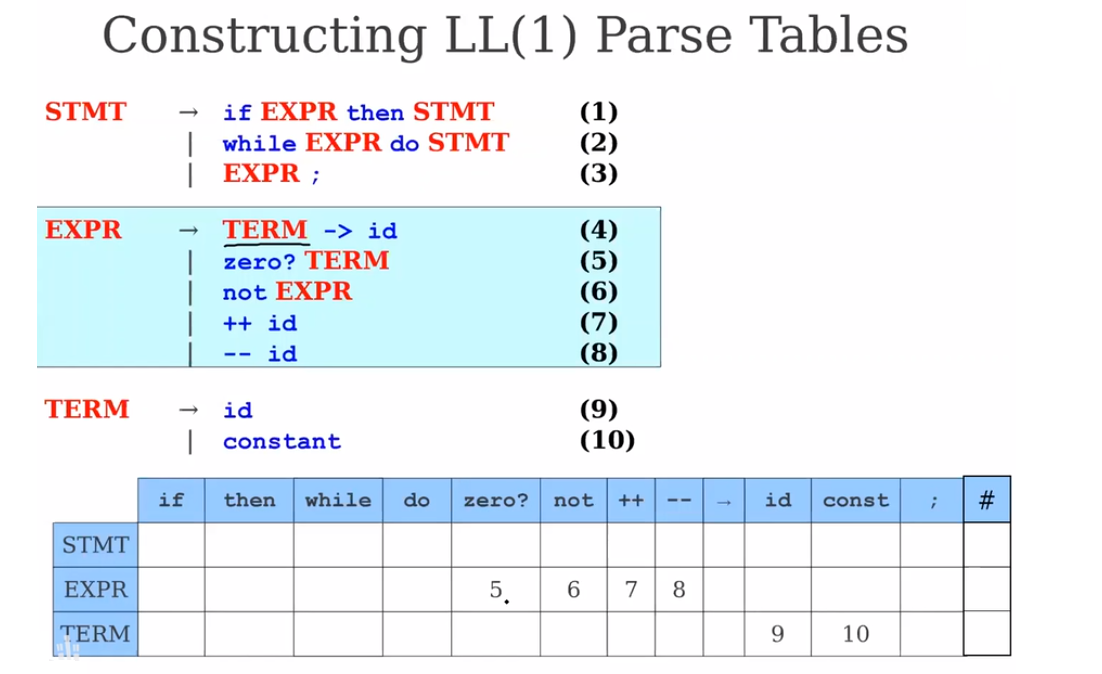
比如说当STMT对应id的匹配的时候,先STMT->EXPR->TERM->id,其中的TERM->id。也就是说考虑当前非终结符经过一步或者多步推出的是唯一的终结符。而不是推出的终结符们存在公共前缀。
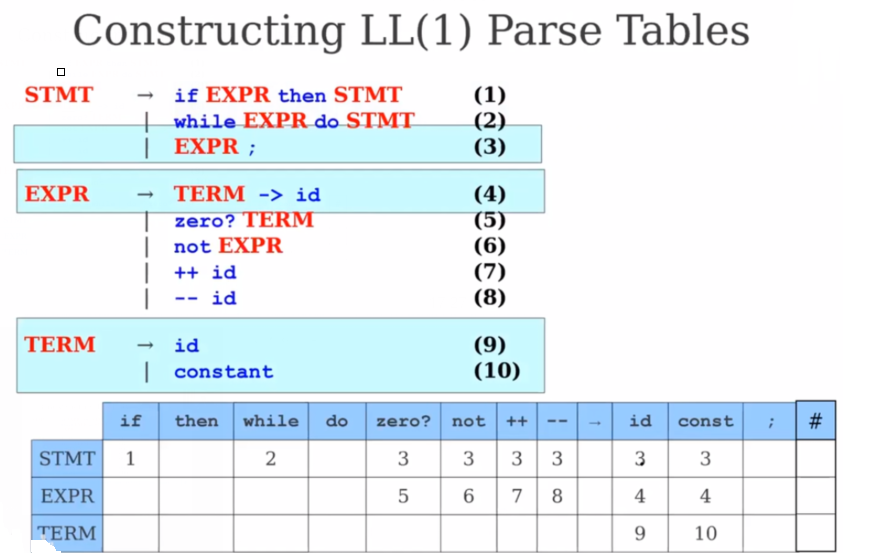
考察 X = > + w {X\stackrel{+}{=>}}w X=>+w,w的首个终结符是唯一的
也就是当A有多个候选式时,当前选中的候选式必须是唯一的。
- 栈顶非终结符与输入终结符a决定所用的(唯一)产生式
- 考察 X = > + w {X\stackrel{+}{=>}}w X=>+w,w的首个终结符是唯一的
由此我们定义首个终结符集合——firstX。
定义:假设α是文法G=(V,T,P,S)的符号串,即A∈V,从A推导出的任意串的首个终结符号集记作
FIRST(A): F I R S T ( A ) = b ∣ A = > + b β , b ∈ T , β ∈ ( V ∪ T ) ∗ {FIRST(A)={b|A \stackrel{+}{=>}b\beta,b∈T,\beta∈(V∪T)^{*}}} FIRST(A)=b∣A=>+bβ,b∈T,β∈(V∪T)∗
特别的,如果 A = > ϵ {A=>\epsilon} A=>ϵ,则 ϵ ∈ F I R S T ( A ) {\epsilon∈FIRST(A)} ϵ∈FIRST(A)。
之后有一个判断两个集合没有交集的方法来判断该文法是不是LL(1)文法。
4.1.7.1.3构建预测分析表(重点)
构建之前至少需要两个集合,一个是first集,一个是follow集合。
对于first集合。手工做法就是画个栈,对每个文法的开头非终结符递归进去,直到搜到非终结符。特别地。如果X=>ε,那么first(X)=ε。同时要考虑对于A->BC,若B->ε,C->a,则first(A)=a。
即如果当前文法能连续前面非终结符能推出ε,则first(A)=first(第一个不能推出ε的非终结符号)。如果该非终结符号的first集合还不知道就递归进去。
多迭代几次直到所有的first集合都不再更新了就结束了。
对于follow集合:
- 若S为开始符号,则FOLLOW(S)包含$.
- 若A->αBβ,若β能推出ε,则follow(B)加上follow(A)∪{first(β)-ε}。不然的话follow(B)就单纯加上first(β)即可
- 若A->αB,则follow(B)加上follow(A)即可。
- 注意这个B可以代表文法推导式子中的任意非终结符。
图片理解:
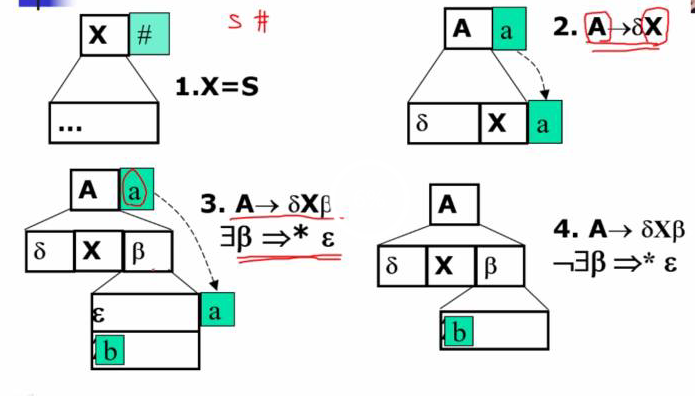
对于构建预测表,两种方式。一种方式是再构造一个select集合。
给定上下文无关文法的产生式A→α, A∈VN,α∈V*。
- 若α不能推导出ε,则SELECT(A→α)=FIRST(α)
- 如果α能推导出ε则:SELECT(A→α)=(FIRST(α) –{ε})∪FOLLOW(A)
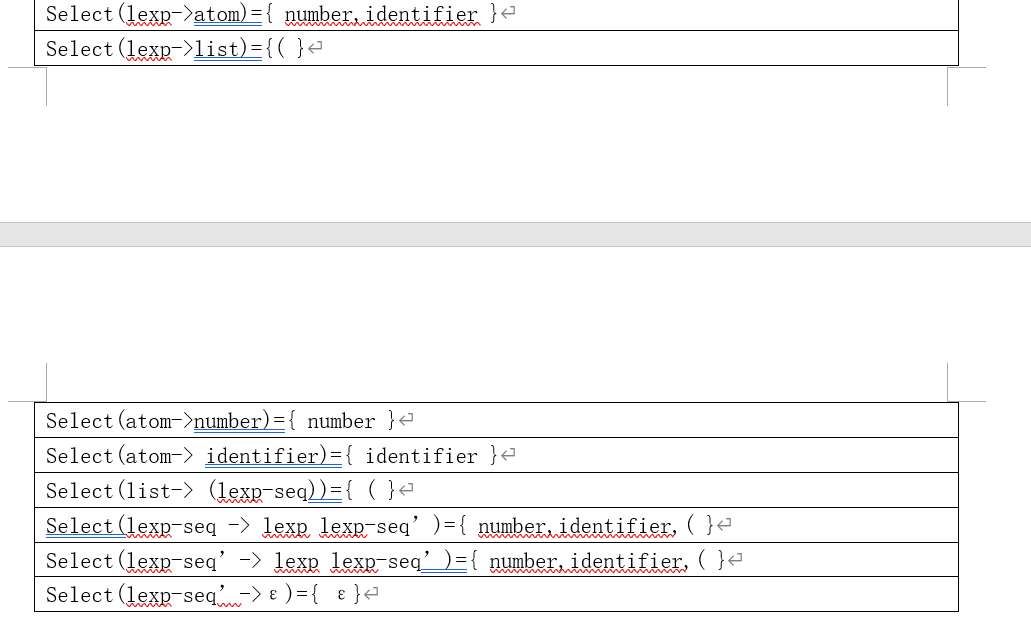
同时注意这样去做会发现一些字符串是没有在推导first集合中出现的,不过这些大概是两种情况。一种是首个字符是终结符。对于首个字符是终结符的串其select就是终结符。
对于多个非终结符的串就是首个非终结符号的first。【比如select(TE’),我们选了first(T)】

- 实例
这个实例来自实验,所以虽然一些样例对了我也不知道first和follow最终是否正确。
① : lexp->atom|list
② :atom->number|identifier
③ :list->(lexp-seq)
④ :lexp-seq->lexp-seq lexp|lexp
① : lexp->atom|list
② :atom->number|identifier
③ :list->(lexp-seq)
④ :lexp-seq->lexp lexp-seq’
⑤ : lexp-seq’->lexp lexp-seq’|ε


| 非终结符 | 输入符号 | |||||
|---|---|---|---|---|---|---|
| ( | number | identifier | ) | ε | ||
| lexp | lexp->list | lexp->atom | lexp->atom | |||
| atom | atom->number | atom->identifier | ||||
| list | list->(lexp-seq) | |||||
| lexp-seq | lexp-seq-> lexp lexp-seq’ | lexp-seq-> lexp lexp-seq’ | lexp-seq-> lexp lexp-seq’ | |||
| lexp-seq’ | lexp-seq’-> lexp lexp-seq’ | lexp-seq’-> lexp lexp-seq’ | lexp-seq’-> lexp lexp-seq’ | |||
| lexp-seq’ | lexp-seq’->ε | |||||
- 举一下课件上的例子方便复习对照
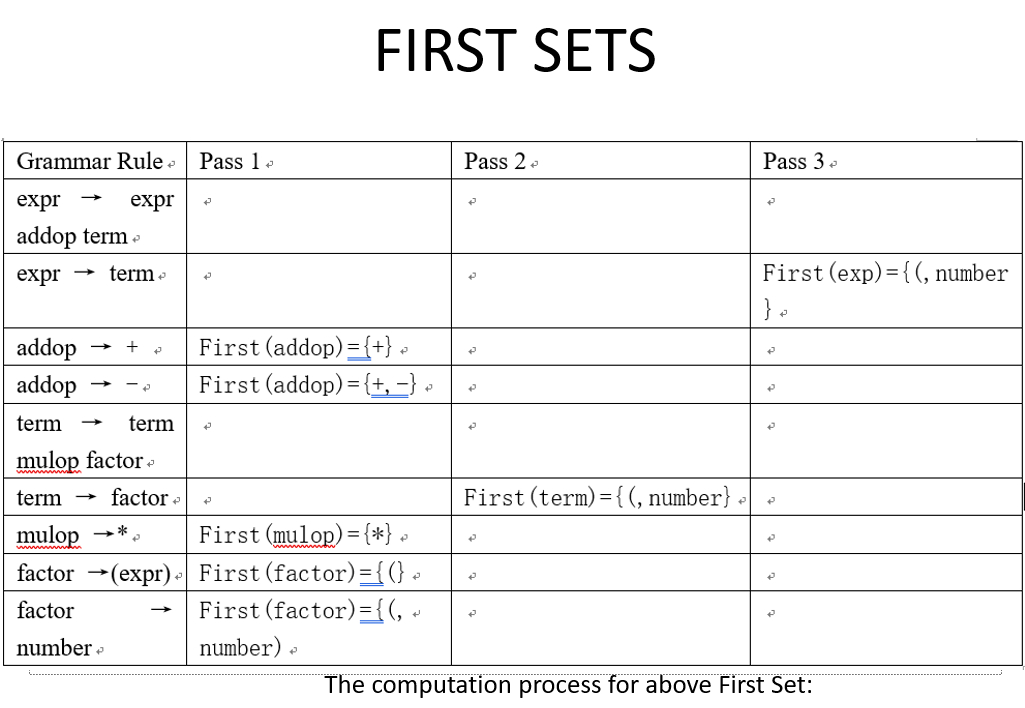



4.1.7.2 递归下降分析法
递归下降就是直接暴力去递归找了。这部分可以直接看实验的代码来理解。