目录
1. 标量无偏估计无参数变换时的CRLB定理
如果要从采集到的一组观测量数据:
![]()
并利用概率密度函数![]() (此时该函数被称为似然函数)去估计未知参数
(此时该函数被称为似然函数)去估计未知参数![]() 。如果
。如果![]() 满足正则条件,即:
满足正则条件,即:
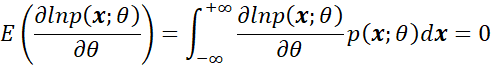
那么对于参数![]() 的任意无偏估计
的任意无偏估计![]() 的方差,满足:
的方差,满足:
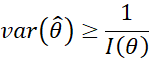
其中:

2. 标量无偏估计有参数变换时的CRLB定理
如果要从采集到的一组观测量数据:
![]()
并利用![]() 估计未知参数
估计未知参数![]() ,且
,且![]() 满足正则条件,此时对于参数
满足正则条件,此时对于参数![]() 的任意无偏估计
的任意无偏估计![]() 的方差,满足CRLB定理,即:
的方差,满足CRLB定理,即:
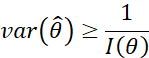
那么参数![]() 经过函数
经过函数![]() 变化后的参数
变化后的参数![]() 的任意无偏估计
的任意无偏估计![]() 的方差满足:
的方差满足:
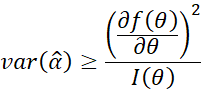
其中:
![]()
3. 标量无偏估计有参数变换时的CRLB证明
首先由于是无偏估计,因此存在:
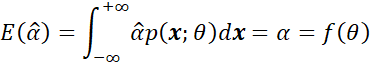
将上式对![]() 进行一阶偏导,可以得到:
进行一阶偏导,可以得到:

除了PDF非零域与未知参数![]() 有关,那么一般可以对上式中的导数与积分互换。可以得到:
有关,那么一般可以对上式中的导数与积分互换。可以得到:
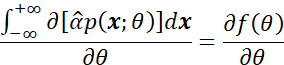
而![]() 中应该只包含采集数据信息,而不包含未知参数
中应该只包含采集数据信息,而不包含未知参数![]() ,因此可以得到:
,因此可以得到:
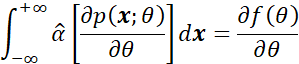
利用对数函数求导的性质,即:
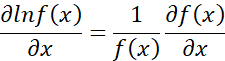
上式转换为:
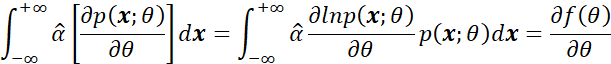
而由正则条件可以得到:

那么两边都乘系数![]() ,得到:
,得到:

因此,两式相减之后可以得到:
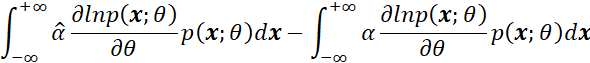

为了能够利用Cauchy-Schwarz不等式,即:
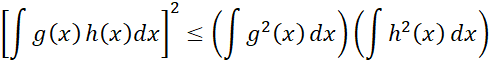
且由于概率密度都大于等于0,因此将上式可以拆分为:
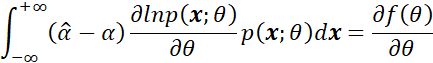

那么利用Cauchy-Schwarz不等式可以得到:
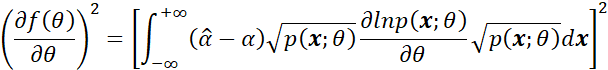
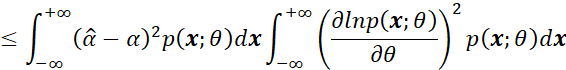
其中:


因此最终可以得到:
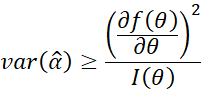
证明完毕。
3. 参数变化后CRLB的具体应用案例与讨论
3.1 用于直接得到参数无变换时的CRLB公式
作为一种简化的参数变化形式,即:
![]()
此时就是参数无变换的特殊情况,带入公式,得到:

这个结果与标量无偏估计的一致,因此参数无变化情况下的CRLB是参数变换CRLB的一种特殊情况。《统计信号处理基础-估计与检测理论》书中附录3A也仅对参数变化后的CRLB定理进行了证明。
3.1.1 例子
用万用表观察直流信号,采集到的数据为:
![]()
其中:
![]()
现在用如下方法估计直流电平![]() :
:
![]()
那么由:

得到:
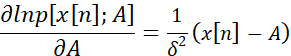
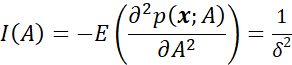
因此:
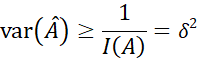
又因为:
![]()
因此无偏估计![]() 还达到了CRLB下限,因此
还达到了CRLB下限,因此![]() 还是最小方差无偏估计。
还是最小方差无偏估计。
3.2 参数线性变换后的CRLB
已知参数θ,其无偏估计![]() 的CRLB为
的CRLB为![]() ,那么参数θ线性变换过得到参数α,一般形式可以表示为:
,那么参数θ线性变换过得到参数α,一般形式可以表示为:
![]()
当选择估计量为:
![]()
可以得到:
![]()
显然,参数线性变换后的估计量,仍然是无偏的。
通过参数变换后的CRLB公式,可以得到![]() 的任意无偏估计方差满足:
的任意无偏估计方差满足:
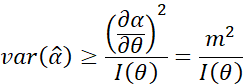
如果![]() 能达到CRLB下限,即:
能达到CRLB下限,即:
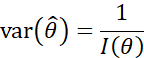
那么进一步可以得到:
![]()
另外,由于:
![]()
因此当估计参数能够达到CRLB下限时,参数线性变换后的也能达到CRLB下限。
于是可以得到结论:参数线性变换能够保持估计量的有效性。
3.2.1 例子
结合上面的例子,如果信号![]() 经过了一个增益为m的理想线性放大器,即:
经过了一个增益为m的理想线性放大器,即:
![]()
而在放大器的输入端,测得:
![]()
且根据上述分析有:
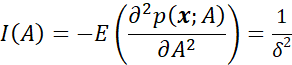
那么经过理想线性放大器之后的输出信号估计的方差满足:
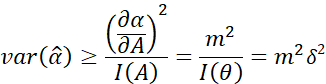
又由于上例中的![]() 为最小方差无偏估计,因此:
为最小方差无偏估计,因此:
![]()
那么存在:
![]()
观察后发现,参数线性变换后的![]() ,也是最小方差无偏估计,线性变换维持了估计参数的有效性。
,也是最小方差无偏估计,线性变换维持了估计参数的有效性。
3.3 参数非线性变换后的CRLB
已知参数![]() ,其无偏估计
,其无偏估计![]() 的CRLB为
的CRLB为![]() ,那么参数
,那么参数![]() 非线性变换过后得到参数
非线性变换过后得到参数![]() 。非线性变换的形式比较多,例如:
。非线性变换的形式比较多,例如:
![]()
![]()
![]()
那么按照参数变换的CRLB公式,任意估计![]() 的方差满足:
的方差满足:
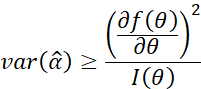
3.3.1 例子
仍然用上面万用表采集直流信号的例子,现在如果估计该直流信号的功率,再已知
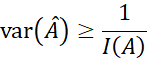
且信号功率的参数变换为:
![]()
那么:
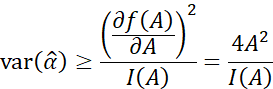
结合上述例子,存在:
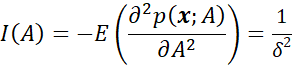
因此:
![]()
而又由于:
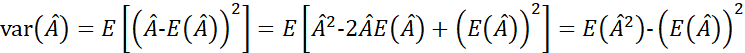
得到:
![]()
因此![]() 不是无偏估计,也就是非线性变换,破坏了原估计量的有效性。
不是无偏估计,也就是非线性变换,破坏了原估计量的有效性。