题目：
如果观测到数据
其中
求A的CRLB。有效估计量存在么，存在的话求方差。
解答：
此题目用标量形式已经推导完毕，现在用矢量参数的形式，再推导一遍，结论应该一致。
首先推导多维高斯分布的矢量形式：
一维情况时，如果
那么
的概率密度函数可以表示为：
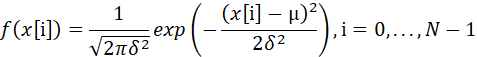
扩展到二维矢量情况时，如果用：
那么存在：
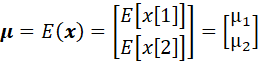
其中
当
独立时，存在：
因此：
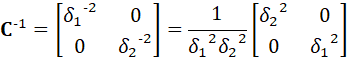
那么：
此时
的概率密度可以用
表示，由于
独立，因此：
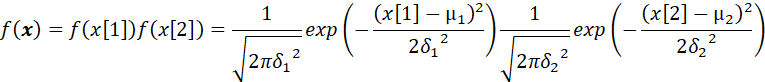
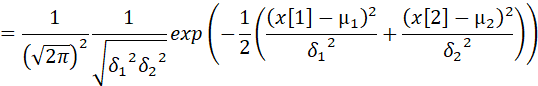
而由于：
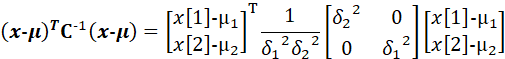
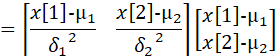
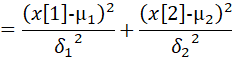
因此：
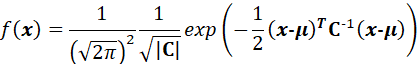
如果推广到N维，那么有：
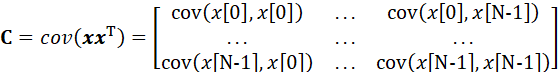
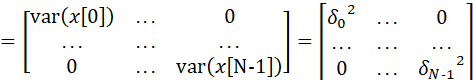
那么x 的概率密度函数，可以表示为：
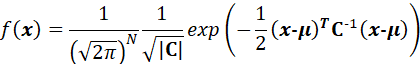
上式就是多维高斯分布的矢量形式。
回到题目，那么：
其中
那么，关于参数A的似然函数可以表示为：
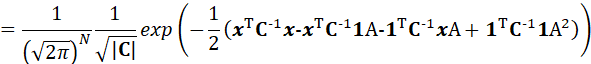
由于A是标量，那么：
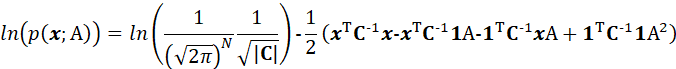
又由于
其中
是对角矩阵，因此似然函数可以进一步表示为：
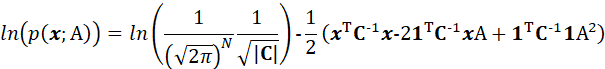
那么：
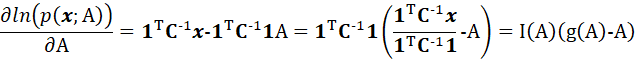
满足达到下限的无偏估计量条件，因此有效估计量存在：
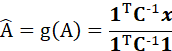
而下限方差可以表示为：
进一步简化，如果
是独立同分布，且方差为
，那么：
那么
因此，无偏估计量可以表示为：
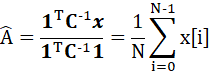
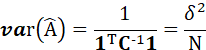
这和用标量结果求得的有效估计量及方差结果一致。