统计信号处理基础 习题解答2-8

题目：

---

对于例2.1描述的问题，利用习题2.3的结果，证明当N→∞ 时，A→A 。为此，对于任意的ε>0，证明： 

 此时的估计量 称为一致（Consistent）估计。如果用另一个估计量：

 代替，考虑一下会发生什么情况。

---

解答：

由习题2-3的结果可知：

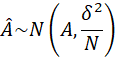
那么：

因此：

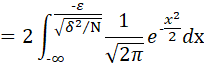
由于当N→∞ 时， ，因此：

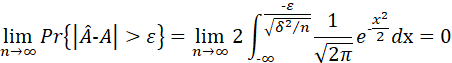
于是可以得到：估计量 称为一致（Consistent）估计。

---

对于估计量 ，可以证明：

 因此 的概率密度函数为：

又由于：

 而

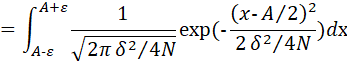
令：

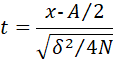
上式变为：

 因此，

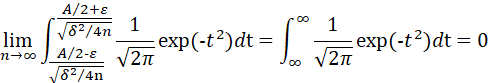
于是有：

下图给出了 的概率密度函数，因此在A=10附近±ε 的概率趋近于0,因此从直观上描述了 趋近于1，估计量 不是一致（Consistent）估计。

​​​​​​​