虽然随机梯度下降仍然是非常受欢迎的优化方法,但其学习过程有时会很慢。Momentum旨在加速学习,特别是处理高曲率、小但一致的梯度,或是带噪声的梯度。Momentum 积累了之前梯度指数级衰减的移动平均,并且继续沿该方向移动。Momentum的效果如下图所示所示:
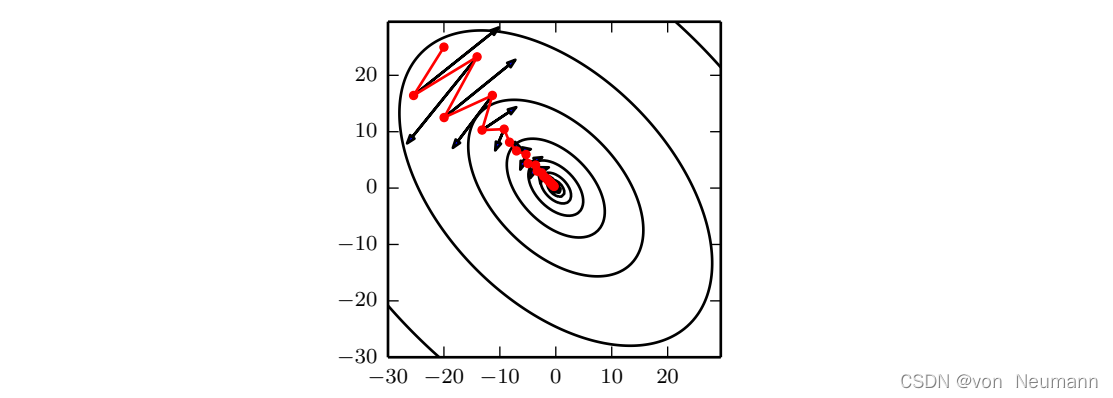
Momentum的主要目的是解决两个问题:Hessian矩阵的病态条件和随机梯度的方差。我们通过此图说明Momentum如何克服这两个问题的第一个。等高线描绘了一个二次损失函数(具有病态条件的Hessian矩阵)。横跨轮廓的红色路径表示Momentum学习规则所遵循的路径,它使该函数最小化。在该路径的每个步骤画一个箭头,表示梯度下降将在该点采取的步骤。可以看到,一个病态条件的二次目标函数看起来像一个长而窄的山谷或具有陡峭边的峡谷。Momentum正确地纵向穿过峡谷,而普通的梯度步骤则会浪费时间在峡谷的窄轴上来回移动。
从形式上看,Momentum引入了变量 v v v充当速度角色——它代表参数在参数空间移动的方向和速率。速度被设为负梯度的指数衰减平均。名称Momentum来自物理类比,根据牛顿运动定律,负梯度是移动参数空间中粒子的力。动量在物理学上定义为质量乘以速度。在Momentum中,我们假设是单位质量,因此速度向量 v v v也可以看作粒子的动量。超参数 α ∈ [ 0 , 1 ) \alpha\in[0,1) α∈[0,1)决定了之前梯度的贡献衰减得有多快。更新规则如下:
v = α v − ϵ ∇ θ ( 1 m ∑ i = 1 m L ( f ( x i ) ) ) θ = θ + v v = \alpha v-\epsilon\nabla_\theta(\frac{1}{m}\sum_{i=1}^mL(f(x^{i})))\\ \theta=\theta+v v=αv−ϵ∇θ(m1i=1∑mL(f(xi)))θ=θ+v
速度 v v v累积了梯度元素 ∇ θ ( 1 m ∑ i = 1 m L ( f ( x i ) ) ) \nabla_\theta(\frac{1}{m}\sum_{i=1}^mL(f(x^{i}))) ∇θ(m1∑i=1mL(f(xi)))。相对于 ϵ \epsilon ϵ, α \alpha α越大,之前梯度对现在方向的影响也越大。
Momentum(Gradient Descent with Momentum, GDM)第 k k k次迭代
输入:学习率 ϵ \epsilon ϵ;初始化参数 θ 0 \theta_0 θ0或第 k − 1 k-1 k−1次输出参数 θ k − 1 \theta_{k-1} θk−1;动量参数 α \alpha α;第 k − 1 k-1 k−1次输出速度 v k − 1 v_{k-1} vk−1
输出:第 k k k次迭代后的参数 θ k \theta_k θk
(1) while 停止准则为满足 \quad\text{停止准则为满足} 停止准则为满足
(2) \quad 从训练集中采包含 m m m个样本 { x ( 1 ) , x ( 2 ) , ⋯ , x ( m ) } \{x^{(1)}, x^{(2)}, \cdots, x^{(m)}\} { x(1),x(2),⋯,x(m)}的小批量,其中 x ( i ) x^{(i)} x(i)对应目标为 y ( i ) y^{(i)} y(i)
(3) \quad 计算梯度估计: g k = 1 m ∇ θ ∑ i L ( f ( x ( i ) ; θ ) , y ( i ) ) g_k = \frac{1}{m}\nabla_\theta\sum_iL(f(x^{(i)}; \theta), y^{(i)}) gk=m1∇θ∑iL(f(x(i);θ),y(i))
(4) v k = α v k − 1 − ϵ g k \quad v_k = \alpha v_{k-1} - \epsilon g_k vk=αvk−1−ϵgk
(5) θ k = θ k − 1 + v \quad\theta_k = \theta_{k-1}+ v θk=θk−1+v
(6) k = k + 1 \quad k = k + 1 k=k+1
(7) return θ k \theta_k θk
之前,步长只是梯度范数乘以学习率。现在,步长取决于梯度序列的大小和排列。当许多连续的梯度指向相同的方向时,步长最大。如果Momentum总是观测到梯度 g g g,那么它会在方向 − g -g −g上不停加速,直到达到最终速度,其中步长大小为:
ϵ ∣ ∣ g ∣ ∣ 1 − α \frac{\epsilon||g||}{1-\alpha} 1−αϵ∣∣g∣∣
因此将Momentum的超参数视为 1 1 − α \frac{1}{1-\alpha} 1−α1有助于理解。例如, α = 0.9 \alpha=0.9 α=0.9对应着最大速度10倍于梯度下降算法。在实践中, α \alpha α的一般取值为0.5、0.9和0.99。和学习率一样, α \alpha α也会随着时间不断调整。一般初始值是一个较小的值,随后会慢慢变大。随着时间推移调整 α \alpha α没有收缩 ϵ \epsilon ϵ重要。
我们可以将Momentum视为模拟连续时间下牛顿动力学下的粒子。这种物理类比有助于直觉上理解Momentum和梯度下降算法是如何表现的。粒子在任意时间点的位置由 θ ( t ) \theta(t) θ(t)给定。粒子会受到净力 f ( t ) f(t) f(t)。该力会导致粒子加速:
f ( t ) = ∂ 2 ∂ t 2 θ f(t)=\frac{\partial^2}{\partial t^2}\theta f(t)=∂t2∂2θ
与其将其视为位置的二阶微分方程,我们不如引入表示粒子在时间t处速度的变量 v ( t ) v(t) v(t),将牛顿动力学重写为一阶微分方程:
v ( t ) = ∂ ∂ t θ ( t ) f ( t ) = ∂ ∂ t v ( t ) v(t)=\frac{\partial}{\partial t}\theta(t)\\ \quad\\ f(t)=\frac{\partial}{\partial t}v(t) v(t)=∂t∂θ(t)f(t)=∂t∂v(t)
由此,Momentum包括通过数值模拟求解微分方程。求解微分方程的一个简单数值方法是欧拉方法,通过在每个梯度方向上小且有限的步来简单模拟该等式定义的动力学。这解释了动量更新的基本形式。力正比于代价函数的负梯度 − ∇ θ J ( θ ) -\nabla_\theta J(\theta) −∇θJ(θ)。该力推动粒子沿着代价函数表面下坡的方向移动。梯度下降算法基于每个梯度简单地更新一步,而使用Momentum的牛顿方案则使用该力改变粒子的速度。我们可以将粒子视作在冰面上滑行的冰球。每当它沿着表面最陡的部分下降时,它会累积继续在该方向上滑行的速度,直到其开始向上滑动为止。另一个力也是必要的。如果代价函数的梯度是唯一的力,那么粒子可能永远不会停下来。想象一下,假设理想情况下冰面没有摩擦,一个冰球从山谷的一端下滑,上升到另一端,永远来回振荡。要解决这个问题,我们添加另一个正比于 − v ( t ) -v(t) −v(t)的力。在物理术语中,此力对应于黏性阻力,就像粒子必须通过一个抵抗介质,如糖浆。这会导致粒子随着时间推移逐渐失去能量,最终收敛到局部极小点。
因为 − v ( t ) -v(t) −v(t)在数学上的便利——速度的整数幂很容易处理。然而,其他物理系统具有基于速度的其他整数幂的其他类型的阻力。例如,颗粒通过空气时会受到正比于速度平方的湍流阻力,而颗粒沿着地面移动时会受到恒定大小的摩擦力。这些选择都不合适。湍流阻力正比于速度的平方,在速度很小时会很弱,不够强到使粒子停下来。非零值初始速度的粒子仅受到湍流阻力,会从初始位置永远地移动下去,和初始位置的距离大概正比于 O ( log t ) O(\log t) O(logt),因此我们必须使用速度较低幂次的力。如果幂次为零,相当于干摩擦,那么力太强了。当代价函数的梯度表示的力很小但非零时,由于摩擦导致的恒力会使得粒子在达到局部极小点之前就停下来。黏性阻力避免了这两个问题——它足够弱,可以使梯度引起的运动直到达到最小,但又足够强,使得坡度不够时可以阻止运动。