卷积层的相关概念 与 卷积层输出图片大小计算

本文内容

常见问题：听课时感觉听懂了，一些代码，发现啥都不懂，各个参数的数值应如何指定呢？

本文会以Pytorch为例，讲解CNN过程中各个参数应如何计算

卷积层的相关概念

• 图片的channel：图片的通道数，例如，当图片是彩色时，通道数为3，分别是RGB。如果图片是黑白的，那么通道数为1。每个通道对应的图片矩阵称为Feature Map，如果是3个通道，即3个Feature Map。

• 卷积的计算过程：见图片
  

• 滤波器（Filter）和卷积核（convolving kernel）：在上图中，
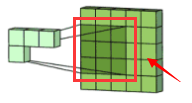
  这玩意称为Kernel。多个卷积核叠加起来组成一个Filter。所以Kernel和Filter的区别是：Kernel是二维的，Filter是三维的，Filter是多个二维的Kernel叠加起来的，所以Filter比Kernel多了一个高度的参数，但由于高度必须和通道数一致，所以一般在代码中不用指定

• Feature Map：每个通道对应的图片矩阵，称为Feature Map，也就是图上黄色矩阵 和红、绿、蓝的那三个大矩阵
  。一个 Filter 会对应生成一个二维的Feature Map。

• stride：步长，只卷积核移动时，一次往前挪动几格

• padding：在原始图片外部填充一圈数值，例如，一个128x128的图片在外围填充一圈数值后，大小变成130x130

• padding_mode：填充的策略，例如：zeros 表示全填0

---

Conv2d使用方法：

torch.nn.Conv2d(in_channels=3, # 输入的channel数
           out_channels=64, # 输出的channel数，即输出的Feature Map数
           kernel_size=3, # 卷积核的长宽
           stride=1, # 步长
           padding=1 # padding大小
           padding_mode='zeros', # 填充策略
           bias=True # Filter也可以有Bias
           )

由于一个Filter对应生成一个Feature Map，而输出Channel数就是输出的Feature Map的数量，所以out_channels也是Filter的数量

扫描二维码关注公众号，回复： 14142324 查看本文章

一个Filter也可以有一个Bias

所以卷积层的参数量为：

$$\text{参数量}=\text{输入Channel数}\times \text{卷积核长}\times \text{卷积核宽}\times \text{Filter数}+\text{Filter的Bias数}$$

对于上面的卷积层为：

$$\text{参数量}=3\times 3\times 3\times 64+64=1792$$

输出的图片尺寸公式为：

$$\text{W或H}=\lfloor (输入大小-卷积核大小+2\times \text{Padding})/\text{stride}\rfloor +1$$

例如，若图片的大小为 128x128，padding为1，stride为2，卷积核为3x3，则输出图片的大小为：

$$输出图片长宽=\lfloor (128-3+2\times 1)/2\rfloor +1=\lfloor 63.5\rfloor +1=64$$

---

案例：数量2张128x128的彩色图片，卷积后输出32个Feature Map，Feature Map的尺寸为64x64

conv = nn.Conv2d(in_channels=3,
           out_channels=32,
           kernel_size=3,
           stride=2,
           padding=1
           )
image = torch.randn(2, 3, 128, 128)
conv(image).size()

torch.Size([2, 32, 64, 64])

---

进阶：卷积核的长宽不一定非要一致，包括卷积过程中右移的步长和下移的步长也不一定一致，甚至上下的padding数和左右的padding也可以不一致。所以源码中kernal_size，stride 和 padding 是可以传 tuple 的

例如：

conv = nn.Conv2d(in_channels=3,
           out_channels=32,
           kernel_size=(3, 4), # 卷积核的尺寸为 3x4
           stride=(2, 4), # 右移步长为2，下移步长为4
           padding=(1, 2) # 左右填充padding数为1，上下填充padding数为2
           )
image = torch.randn(2, 3, 128, 128)
conv(image).size()

torch.Size([2, 32, 64, 33])

上面例子中，最终Feature Map的宽计算公式为：

$$W=\lfloor (128-3+2\times 1)/2\rfloor +1=\lfloor 63.5\rfloor +1=64$$

高的计算公式为：

$$H=\lfloor (128-4+2\times 2)/4\rfloor +1=33$$

所以最终的Feature Map的尺寸为 64x33

---

参考资料

CNN中feature map、卷积核、卷积核个数、filter、channel的概念解释，以及CNN 学习过程中卷积核更新的理解：https://blog.csdn.net/xys430381_1/article/details/82529397