上一篇:03 梯度(Gradient)很小怎么办(Local Minima与Saddle Point)-学习笔记-李宏毅深度学习2021年度
下一篇:05 Classification-学习笔记-李宏毅深度学习2021年度
本节内容及相关链接
自动调整 Learning Rate 的常见策略
课堂笔记
当training陷入瓶颈时,不一定是gradient太小,有可能是由于学习率太大,导致其在山谷之间震荡,无法抵达最小值
对应到gradient的函数图像如下图:
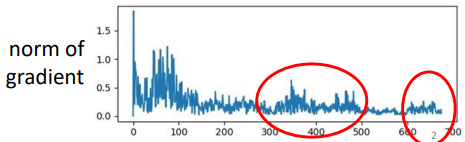
x x x 轴为更新次数, y y y 为gradient的大小
要根据迭代次数,当前梯度等因素,自动调整 Learning Rate。 θ \theta θ 的更新公式改为: θ i t + 1 ← θ i t − η σ i t g i t \theta_i^{t+1}\leftarrow \theta_i^t - \frac{\eta}{\sigma_i^t}g^t_i θit+1←θit−σitηgit
对于Learning Rate的调整,都是通过调整 σ \sigma σ 来实现
常见的调整策略有:
- Root Mean Square:考虑本次的梯度和过去的所有梯度
- RMSProp:重点考虑本次的梯度,稍微考虑过去的所有梯度
- Adam:结合了RMSProp和Momentum
- Learning Rate Decay:随着更新次数的增多,因为我们就会越接近目标,所以要将Learning Rate调小
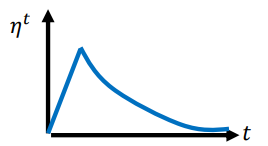
- Warm Up:一开始Learning Rate小一点,然后随着迭代次数增多而增大,然后到某一个点时,再随着迭代次数增多而减小。如图所示:
Root Mean Square公式为: σ i t = 1 t + 1 ∑ i = 0 t ( g i t ) 2 \sigma_{i}^{t}=\sqrt{\frac{1}{t+1} \sum_{i=0}^{t}\left(g_{i}^{t}\right)^{2}} σit=t+11i=0∑t(git)2
RMSProp公式为: σ i t = α ( σ i t − 1 ) 2 + ( 1 − α ) ( g i t ) 2 \sigma_{i}^{t}=\sqrt{\alpha\left(\sigma_{i}^{t-1}\right)^{2}+(1-\alpha)\left(g_{i}^{t}\right)^{2}} σit=α(σit−1)2+(1−α)(git)2 其中 α \alpha α 为要调的超参数, 0 < α < 1 0<\alpha<1 0<α<1
Adam 建议采用Pytorch默认的参数。
Adam的调整策略如下:
