图神经网络（一）图信号处理与图卷积神经网络（4）图滤波器

0. 图滤波器

有了上一节中图信号的频率定义之后，接下来我们就可以对图滤波器（Graph Filter）进行定义了。¹类比于离散型号处理，在图信号处理中，我们将图滤波器定义为对给定图信号的频谱中各个频率分量的强度进行增强或衰减的操作。假设图滤波器为$H\in R^{N\times N}$，则$H$:$R^N\to R^N$，令输出图信号为$\mathbf{y}$，则：
$$\mathbf{y}=H\mathbf{x}=\sum _{k=1}^N(h({\lambda }_k){\tilde{x}}_k){\mathbf{v}}_k$$ 对比上一节的逆图傅里叶变换的展开向量形式的公式，我们可以清楚地看到增强还是衰减是通过h(λ)项来控制的。为了进一步看清楚H的形式，我们需要对上式进行变换：
$$\begin{array}{rl}\mathbf{y}& =H\mathbf{x}=\sum _{k=1}^N(h({\lambda }_k){\tilde{x}}_k){\mathbf{v}}_k=\left[\begin{array}{cccc}⋮& ⋮& \cdots & ⋮\\ {\mathbf{v}}_1& {\mathbf{v}}_2& \cdots & {\mathbf{v}}_N\\ ⋮& ⋮& \cdots & ⋮\end{array}\right]\left[\begin{array}{c}h({\lambda }_1){\tilde{x}}_1\\ h({\lambda }_2){\tilde{x}}_2\\ ⋮\\ h({\lambda }_N){\tilde{x}}_N\end{array}\right]\\ & =V\left[\begin{array}{ccc}h({\lambda }_1)& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & h({\lambda }_N)\end{array}\right]\left[\begin{array}{c}{\tilde{x}}_1\\ ⋮\\ {\tilde{x}}_N\end{array}\right]\\ & =V\left[\begin{array}{ccc}h({\lambda }_1)& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & h({\lambda }_N)\end{array}\right]V^{\text{T}}\mathbf{x}\end{array}$$于是得到：
$$H=V\left[\begin{array}{ccc}h({\lambda }_1)& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & h({\lambda }_N)\end{array}\right]V^{\text{T}}=V{\Lambda }_h{V}^{\text{T}}$$ 相较于拉普拉斯矩阵，$H$仅仅改动了对角矩阵上的值，因此，$H$具有以下形式：$H_{ij}=0$，如果$i\ne j$或者$e_{ij}\ne E$。也就是说，$H$矩阵只在对角与边坐标上时才可能取非零值。从算子角度来看，$H\mathbf{x}$描述了一种作用在每个节点一阶子图上的变换操作。一般来说，我们称满足上述性质的矩阵为$G$的图位移算子（Graph Shift Operator），拉普拉斯矩阵与邻接矩阵都是典型的图位移算子。事实上，本章讲解的所有图信号处理的相关理论，都可以被扩展到图位移算子上，并不局限在拉普拉斯矩阵上。

 图滤波器具有以下性质：

 (1) 线性：$H(\mathbf{x}+\mathbf{y})=H\mathbf{x}+H\mathbf{y}$；

 (2) 滤波操作是顺序无关的：$H_1(H_2\mathbf{x})=H_2(H_1\mathbf{x})$；

 (3) 如果$h(\lambda )\ne 0$，则该滤波操作是可逆的。

 我们称${\Lambda }_h$为图滤波器$H$的频率响应矩阵，对应的函数$h(\lambda )$为$H$的频率响应函数，不同的频率响应函数可以实现不同的滤波效果。在信号处理中，常见的滤波器有3类：低通滤波器、高通滤波器、带通滤波器。

图1 3类滤波器的频率响应函数

 图1所示为3类滤波器的频率响应函数：从a图可以看出，低通滤波器只保留信号中的低频部分，更加关注信号中平滑的部分；从b图中可以看出，高通滤波器只保留信号中的高频部分，更加关注信号中快速变化的部分；从c图中可以看出，带通滤波器只保留信号特定频段的成分。

 理论上，我们希望实现任意性质的图滤波器，也就是实现任意类型函数曲线的频率响应函数。通过逼近理论，我们可以用泰勒展开——多项式逼近函数去近似任意函数。下面，我们将目光聚焦在拉普拉斯矩阵多项式拓展形式的图滤波器上：
$$H=h_0{L}^0+h_1{L}^1+h_2{L}^2+\cdots +h_K{L}^K=\sum _{k=0}^K{h}_k{L}^k$$ 其中$K$是图滤波器$H$的阶数。和图信号一样，对于图滤波器，我们也可以同时从空域视角和频域视角来理解。

1. 空域视角

 对于$\mathbf{y}=H\mathbf{x}={\sum }_{k=0}^K{h}_k{L}^k\mathbf{x}$，如果我们设定：
$${\mathbf{x}}^{(k)}=L^k\mathbf{x}=L{\mathbf{x}}^{(k-1)}$$ 则：
$$\mathbf{y}=\sum _{k=0}^K{\mathbf{h}}_k{\mathbf{x}}^{(k)}$$ 通过上式，将输出图信号变成了$(K+1)$组图信号的线性加权。对于式(5)，由于$L$是一个图位移算子，因此，${\mathbf{x}}^{(k-1)}$到${\mathbf{x}}^{(k)}$的变换只需要所有节点的一阶邻居参与计算。总的来看，${\mathbf{x}}^{(k)}$的计算只需要所有节点的$k$阶邻居参与，我们称这种性质为图滤波器的局部性。

 从空域角度来看，滤波操作具有以下性质：

 (1) 具有局部性，每个节点的输出信号值只需要考虑其$K$阶子图；

 (2) 可通过$K$步迭代式的矩阵向量乘法来完成滤波操作。

 我们以图2为例来看图信号滤波操作在空域的计算过程：

图2 空域视角滤波计算示意图

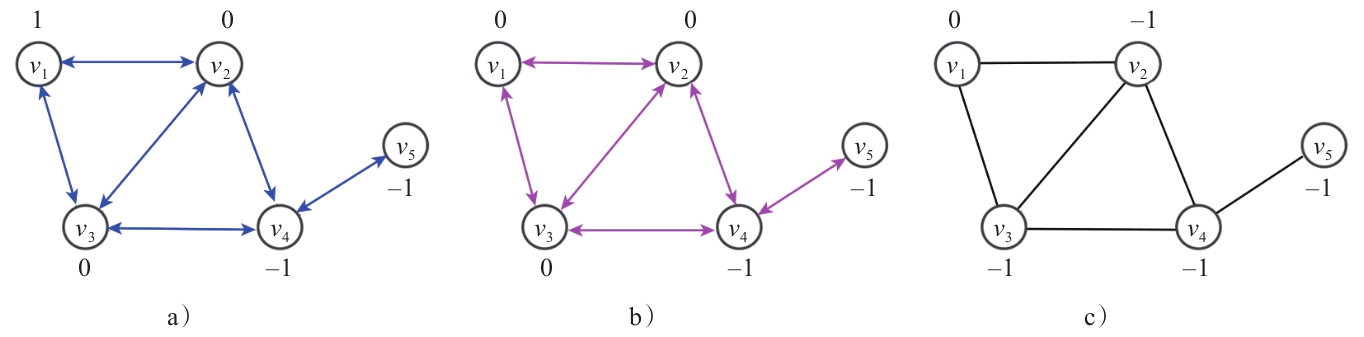
 首先将图G的邻接矩阵作为图滤波器：
$$H=A=\left[\begin{array}{ccccc}0& 1& 1& 0& 0\\ 1& 0& 1& 1& 0\\ 1& 1& 0& 1& 0\\ 0& 1& 1& 0& 1\\ 0& 0& 0& 1& 0\end{array}\right]$$

 给定图信号$\mathbf{x}={\left[\begin{array}{ccccc}1& 0& 0& -1& -1\end{array}\right]}^{\text{T}}$，系数向量$\mathbf{h}={\left[\begin{array}{ccc}1& 0.5& 0.5\end{array}\right]}^{\text{T}}$，根据公式$\mathbf{y}={\sum }_{k=0}^K{\mathbf{h}}_k{\mathbf{x}}^{(k)}$，我们可以得到滤波输出的图信号为：
$$\mathbf{y}=h_0{\mathbf{x}}^{(0)}+h_1{\mathbf{x}}^{(1)}+h_2{\mathbf{x}}^{(2)}$$ 其中$$\begin{array}{rl}& {\mathbf{x}}^{(0)}=\mathbf{x}={\left[\begin{array}{ccccc}1& 0& 0& -1& -1\end{array}\right]}^{\text{T}}，\\ & {\mathbf{x}}^{(1)}=H\mathbf{x}={\left[\begin{array}{ccccc}0& 0& 0& -1& -1\end{array}\right]}^{\text{T}}，\\ & {\mathbf{x}}^{(2)}=H{\mathbf{x}}^{(1)}={\left[\begin{array}{ccccc}0& -1& -1& -1& -1\end{array}\right]}^{\text{T}}。\end{array}$$ 带入数据，得到$\mathbf{y}$：
$$\begin{array}{rl}\mathbf{y}& =1\mathbf{x}+0.5{\mathbf{x}}^{(1)}+0.5{\mathbf{x}}^{(2)}\\ & =\left[\begin{array}{c}1\\ 0\\ 0\\ -1\\ -1\end{array}\right]+0.5\left[\begin{array}{c}0\\ 0\\ 0\\ -1\\ -1\end{array}\right]+0.5\left[\begin{array}{c}0\\ -1\\ -1\\ -1\\ -1\end{array}\right]\\ & =\left[\begin{array}{c}1\\ -0.5\\ -0.5\\ -2\\ -2\end{array}\right]\end{array}$$ ${\mathbf{x}}^{(1)}$、${\mathbf{x}}^{(2)}$的计算在图2中已给出，由于空域滤波操作的局部性，$H$等价于一个聚合邻居的操作算子，如a图、b图中的箭头所示，从a图、b图、c图中可以清楚地看出，${\mathbf{x}}^{(0)}\to {\mathbf{x}}^{(1)}\to {\mathbf{x}}^{(2)}$的计算是一个迭代式的过程。

2. 频域角度

 $H$由于$L=V\Lambda V^{\text{T}}$，则：
$$\begin{array}{rl}H& =\sum _{k=0}^K{h}_k{L}^k\\ & =\sum _{k=0}^K{h}_k(V\Lambda V^{\text{T}}{)}^k\\ & =V\left(\sum _{k=0}^K{h}_k{\Lambda }^k\right)V^{\text{T}}\\ & =V\left[\begin{array}{ccc}{\sum }_{k=0}^K{h}_k{\lambda }_1^k& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & {\sum }_{k=0}^K{h}_k{\lambda }_N^k\end{array}\right]\end{array}$$ 通过上式，我们可以清楚地看出$H$的频率响应函数为$\lambda$的$K$次代数多项式，如果$K$足够大，我们可以用这种形式去逼近任意一个关于$\lambda$的函数。

 如果我们用该滤波器进行类别，则：
$$\mathbf{y}=H\mathbf{x}=V\left(\sum _{k=0}^K{h}_k{\Lambda }^k\right)V^{\text{T}}\mathbf{x}$$ 上式即为频域视角下的滤波操作，其变换过程由以下3步组成：

 (1) 通过傅里叶变换，即$V^{\text{T}}\mathbf{x}$将图信号变换到频域空间；

 (2) 通过${\Lambda }^k={\sum }_{k=0}^K{h}_k{\Lambda }^k$对频率分量的强度进行调节，得到$\tilde{\mathbf{y}}$；

 (3) 通过逆图傅里叶变换，即$V\tilde{\mathbf{y}}$将$\tilde{\mathbf{y}}$反解成图信号$\mathbf{y}$。

 我们假设所有的多项式系数$h_k$构成向量$h$，则$H$的频率响应矩阵为：
$${\Lambda }^k=\sum _{k=0}^K{h}_k{\Lambda }^k=\text{diag}(\Psi \mathbf{h})$$ 其中:
$$\Psi =\left[\begin{array}{cccc}1& {\lambda }_1& \cdots & {\lambda }_1^K\\ 1& {\lambda }_2& \cdots & {\lambda }_2^K\\ ⋮& ⋮& \ddots & ⋮\\ 1& {\lambda }_N& \cdots & {\lambda }_N^K\end{array}\right]$$为范德蒙矩阵，我们可以反解的带多项式系数：
$$h={\Psi }^{-1}{\text{diag}}^{-1}({\Lambda }^k)$$其中，${\text{diag}}^{-1}$表示将对角矩阵编程列向量。

 上式说明给定我们想要的频率响应矩阵，可以通过上式反解得到多项式系数。显然，这个十字对于特定性质的图滤波器的设计具有十分重要的意义。

 图3是对图信号进行低通滤波的操作示意图。从中可以看到，相较于原始图信号，对其进行低通滤波后，图信号变得更加平滑了。

图3 频域滤波过程示意图

 从频域角度来看，我们可以对图滤波操作作出以下性质总结：

 (1) 从频域视角能够更加清晰地完成对图信号的特定滤波操作；

 (2) 图滤波器如何设计具有显式的公式指导；

 (3) 对矩阵进行特征分解是一个非常耗时的操作，具有$O(N^3)$的时间复杂度，相比空域视角中的矩阵向量乘法而言，有工程上的局限性。

参考文献

---

1. [1] 刘忠雨, 李彦霖, 周洋.《深入浅出图神经网络: GNN原理解析》.机械工业出版社. ↩︎