深度学习之强化学习（1）强化学习案例

人工智能=深度学习+强化学习——David Silver

 强化学习时机器学习领域除有监督学习、无监督学习外的另一个研究分支，它主要利用智能体与环境进行交互，从而学习到能获得良好结果的策略。与有监督学习不同，强化学习的动作并没有明确的标注信息，只有来自环境的反馈的奖励信息，它通常具有一定的滞后性，用于反映动作的“好与坏”。

 随着深度学习神经网络的兴起，强化学习这一领域也获得了蓬勃的发展。2015年，英国DeepMind公司提出了基于深度神经网络的强化学习DQN，在太空入侵者、打砖块、乒乓球等49个Atari游戏中取得了与人类相当的游戏水平；2017年，DeepMind提出的AlphaGo程序以3:0的比分战胜当时围棋世界排名第一的选手柯洁；同年，AlphaGo的新版本AlphaGo Zero在无任何人类知识的条件下，通过自我博弈训练的方式以100:0战胜了AlphaGo；2019年，OpenAI Five程序以2:0战胜Dota2世界冠军OG队伍，尽管这次比赛的游戏规则有所限制，但是对于Dota2这种对于需要超强个体只能水平和良好团队协作的游戏，这次胜利无疑再次坚定了人类对于AGI的信念。

 本章我们将介绍强化学习中的主流算法，其中包含在太空入侵者等游戏上取得类人水平的DQN算法、制胜Dota2的主要功臣PPO算法等。

强化学习案例

 强化学习算法的设计与传统的有监督学习不太一样，包含了大量的新的数学公式推导。在进入强化学习算法的学习过程之前，我们先通过一个简单的例子来感受强化学习算法的魅力。

 此节不需要掌握每个细节，以直观感受为主，获得第一印象即可。

1. 平衡杆游戏

 平衡杆游戏系统包含了三个物体：滑轨、小车和杆。如图1所示，小车可以自由在滑轨上移动，杆的一侧通过轴承固定在小车上。在初始状态，小车位于滑轨中央，杆竖直立在小车上，智能体通过控制小车的左右移动来控制杆的平衡，当杆与竖直方向的角度大于某个角度或者小车偏离滑轨中心位置一定距离后视为游戏结束。游戏时间越长，游戏给予的回报也就越多，智能体的操控水平也越高。

图1. 平衡杆游戏系统

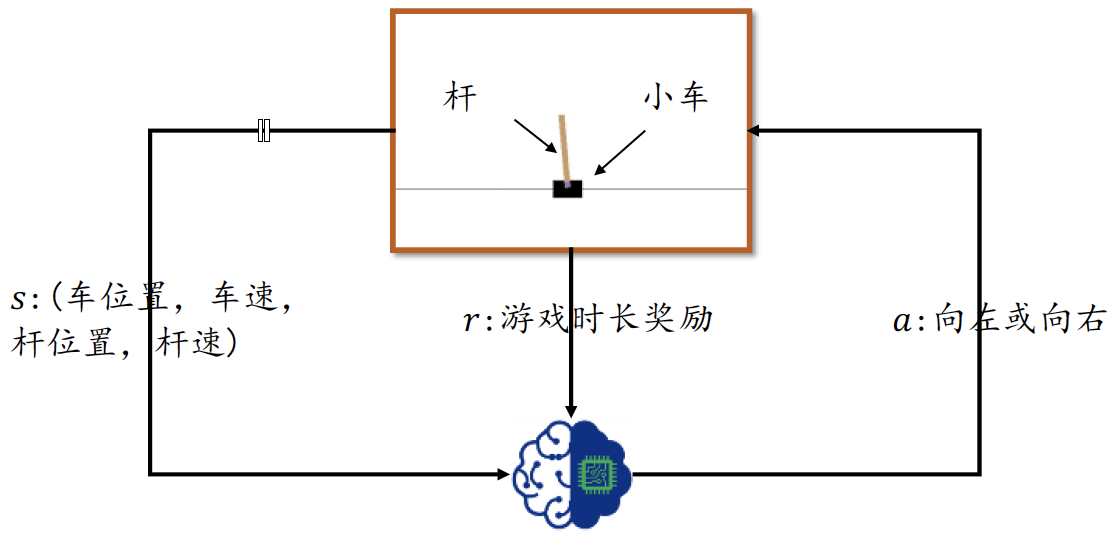
 为了简化环境状态的表示，我们这里直接取高层的环境特征向量s作为智能体的输入，它一共包含了四个高层特征，分别为：小车位置、小车速度、杆角度和杆的速度。智能体的输出动作$a$为向左移动或者向右移动，动作施加在平衡杆系统上会产生一个新的状态，同时系统也会返回一个奖励值，这个奖励值可以简单的记为1，即时长加1。在每个时间戳$t$上面，智能体通过观察环境状态$s_t$而产生动作$a_t$，环境接收动作后状态改变为$s_{t+1}$，并返回奖励$r_t$。

2. 策略网络

 下面我们来探讨强化学习中最为关键的环节：如何判断和决策？我们把判断和决策叫做策略（Policy）。策略的输入是状态$s$，输出为某具体的动作$a$或动作的分布${\pi }_{\theta }(a|s)$，其中$\theta$为策略函数$\pi$的参数，可以利用神经网络来参数化${\pi }_{\theta }$函数，如图2所示：

图2. 策略网络

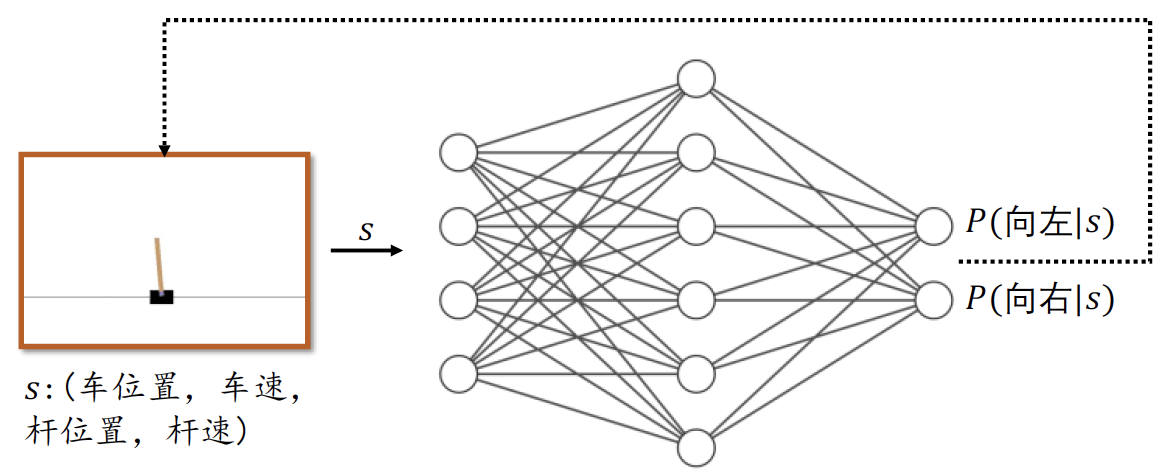
 图中神经网络${\pi }_{\theta }$的输入为平衡杆系统的状态$s$，即长度为4的向量，输出为所有动作的概率${\pi }_{\theta }(a|s)$：向左的概率$P(向左|s)$和向右的概率$P(向右|s)$，并满足所有动作概率之和为1的关系：
$$\sum _{a\in A}{\pi }_{\theta }(a|s)=1$$
其中$A$为所有动作的集合。${\pi }_{\theta }$网络代表了智能体的策略，称为策略网络。很自然地，我们可以将策略函数具体化为输入节点为4个，中间多个全连接隐藏层，输出层的输出节点数为2的神经网络，代表了这两个动作的概率分布。在交互时，选择概率最大的动作
$$a_t=\underset{a}{\mathrm{argmax}}{\pi }_{\theta }(a|s_t)$$
作为决策结果，作用与环境中，并得到新的状态$s_{t+1}$和奖励$r_t$，如此循环往复，直至游戏回合结束。

 我们将策略网络实现为一个2层的全连接网络，第一层将长度为4的向量转换为长度为128的向量，第二层将128的向量转换为2的向量，即动作的概率分布。和普通的神经网络的创建过程一样，代码如下：

class Policy(keras.Model):
    # 策略网络，生成动作的概率分布
    def __init__(self):
        super(Policy, self).__init__()
        self.data = [] # 存储轨迹
        # 输入为长度为4的向量，输出为左、右2个动作，指定W张量的初始化方案
        self.fc1 = layers.Dense(128, kernel_initializer='he_normal')
        self.fc2 = layers.Dense(2, kernel_initializer='he_normal')
        # 网络优化器
        self.optimizer = optimizers.Adam(lr=learning_rate)

    def call(self, inputs, training=None):
        # 状态输入s的shape为向量：[4]
        x = tf.nn.relu(self.fc1(inputs))
        x = tf.nn.softmax(self.fc2(x), axis=1)  # 获得动作的概率分布
        return x

 在交互时，我们将每个时间戳上的状态输入$s_t$，动作分布输出$a_t$，环境奖励$r_t$和新状态$s_{t+1}$作为一个4元组item记录下来，用于策略网络的训练。代码如下：

def put_data(self, item):
    # 记录r,log_P(a|s)
    self.data.append(item)

3. 梯度更新

 如果需要利用梯度下降算法来优化网络，需要知道每个输入$s_t$的标注信息$a_t$，并且确保从输入到损失值是连续可导的。但是强化学习与传统的有监督学习并不相同，主要体现为强化学习在每一个时间戳$t$上面的动作$a_t$并没有一个明确的好与坏的标准，奖励$r_t$可以在一定程度上反映动作的好坏，但不能直接决定动作的好坏，甚至有些游戏交互过程只有一个最终的代表游戏结果的奖励$r_t$信号，如围棋。那么给每个状态定义一个最优动作$a_t^{\ast }$作为神经网络输入$s_t$的标注可行吗？首先是游戏中的状态总数通常是巨大的，如围棋的状态数共有约$10^{170}$之多。再者每个状态很难定义一个最优动作，有些动作虽然短期回报不高，但是长期回报却是较好的，而且有时候甚至连人类自己都不知道哪个动作才是最优的。

 因此，策略的优化目标不应该是让输入$s_t$的输出尽可能地逼近标注动作，而是要最大化总回报的期望值。总回报可以定义为从游戏会和开始到游戏结束前的激励之和$\sum r_t$ 。一个好的策略，应能够在环境上面取得的总的回报的期望值$J({\pi }_{\theta })$最高。根据梯度上升算法的原理，我们如果能够求出$\frac{\partial J(\theta )}{\partial \theta }$，那么策略网络只需要按照
$${\theta }^{\prime }=\theta +\eta \cdot \frac{\partial J(\theta )}{\partial \theta }$$
即可迭代优化策略网络，从而忽的较大的期望总回报。

 很遗憾的是，总回报期望$J(\theta )$是由游戏环境给出的，如果无法得知环境模型，那么$\frac{\partial J(\theta )}{\partial \theta }$是不能通过自动微分计算的。那么即使$J(\theta )$表达式未知，能不能直接求解偏导数$\frac{\partial J(\theta )}{\partial \theta }$呢？

 答案是肯定的。我们这里直接给出$\frac{\partial J(\theta )}{\partial \theta }$的推导结果，具体的推导过程会在梯度推导的小节里详细介绍：
$$\frac{\partial J(\theta )}{\partial \theta }={\mathbb{E}}_{\tau \sim p_{\theta }(\tau )}\left[\right(\sum _{t=1}^T\frac{\partial }{\partial \theta }\text{log}{\pi }_{\theta }(a_t│s_t))R(\tau )]$$
利用上式，只需要计算出$\frac{\partial }{\partial \theta }\text{log}{\pi }_{\theta }(a_t│s_t)$，并乘以$R(\tau )$即可更新出$\frac{\partial J(\theta )}{\partial \theta }$，按照${\theta }^{\prime }=\theta -\eta \cdot \frac{\partial \mathcal{L}(\theta )}{\partial \theta }$方式更新策略网络，即可最大化$J(\theta )$函数。其中$R(\tau )$为某次交互的总回报，$\tau$为交互轨迹$s_1,a_1,r_1,s_2,a_2,r_2,\dots ,s_T$，$T$是交互的时间戳数量或步数，$\text{log}{\pi }_{\theta }(a_t│s_t)$为策略网络的输出中$a_t$动作的概率值取$\text{log}$函数，$\text{log}{\pi }_{\theta }(a_t│s_t)$可以通过TensorFlow自动微分求解出网络的梯度，这一部分是连续可导的。

 损失函数的代码实现为：

for r, log_prob in self.data[::-1]:  # 逆序取轨迹数据
    R = r + gamma * R  # 累加计算每个时间戳上的回报
    # 每个时间戳都计算一次梯度
    # grad_R=-log_P*R*grad_theta
    loss = -log_prob * R

完整的训练及更新代码如下：

def train_net(self, tape):
    # 计算梯度并更新策略网络参数。tape为梯度记录器
    R = 0  # 终结状态的初始回报为0
    for r, log_prob in self.data[::-1]:  # 逆序取轨迹数据
        R = r + gamma * R  # 累加计算每个时间戳上的回报
        # 每个时间戳都计算一次梯度
        # grad_R=-log_P*R*grad_theta
        loss = -log_prob * R
        with tape.stop_recording():
            # 优化策略网络
            grads = tape.gradient(loss, self.trainable_variables)
            # print(grads)
            self.optimizer.apply_gradients(zip(grads, self.trainable_variables))
    self.data = []  # 清空轨迹

4. 平衡杆游戏实战

我 们一共训练400个回合，在回合的开始，复位游戏状态，通过送入输入状态来采样动作，从而与环境进行交互，并记录每一个时间戳的信息，直至游戏回合结束。

 交互和训练部分代码如下：

for n_epi in range(400):
    s = env.reset()  # 回到游戏初始状态，返回s0
    with tf.GradientTape(persistent=True) as tape:
        for t in range(501):  # CartPole-v1 forced to terminates at 500 step.
            # 送入状态向量，获取策略
            s = tf.constant(s, dtype=tf.float32)
            # s: [4] => [1,4]
            s = tf.expand_dims(s, axis=0)
            prob = pi(s)  # 动作分布:[1,2]
            # 从类别分布中采样1个动作, shape: [1]
            a = tf.random.categorical(tf.math.log(prob), 1)[0]
            a = int(a)  # Tensor转数字
            s_prime, r, done, info = env.step(a)
            # 记录动作a和动作产生的奖励r
            # prob shape:[1,2]
            pi.put_data((r, tf.math.log(prob[0][a])))
            s = s_prime  # 刷新状态
            score += r  # 累积奖励

            if n_epi >1000:
                env.render()
                # im = Image.fromarray(s)
                # im.save("res/%d.jpg" % info['frames'][0])

            if done:  # 当前episode终止
                break
        # episode终止后，训练一次网络
        pi.train_net(tape)
    del tape

模型的训练过程如图3所示，横轴为训练回合数量，纵轴为回合的平均回报值。可以看到随着训练的进行，网络获得的平均回报越来越高，策略越来越好。实际上，强化学习算法对参数及其敏感，甚至修改随机种子都会导致截然不同的性能表现，在实现的过程中需要精调参数才能发挥出算法的潜力。

图3. 平衡杆游戏训练过程

 通过这个例子，我们对强化学习算法和强化学习的交互过程有了初步的印象和了解，接下来我们来正式化描述强化学习问题。

完整代码

import gym
import os
import numpy as np
import matplotlib
from matplotlib import pyplot as plt
# Default parameters for plots
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers, optimizers, losses
from PIL import Image

matplotlib.rcParams['font.size'] = 18
matplotlib.rcParams['figure.titlesize'] = 18
matplotlib.rcParams['figure.figsize'] = [9, 7]
matplotlib.rcParams['font.family'] = ['KaiTi']
matplotlib.rcParams['axes.unicode_minus'] = False

env = gym.make('CartPole-v1')  # 创建游戏环境
env.seed(2333)
tf.random.set_seed(2333)
np.random.seed(2333)
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'
assert tf.__version__.startswith('2.')

learning_rate = 0.0002
gamma = 0.98


class Policy(keras.Model):
    # 策略网络，生成动作的概率分布
    def __init__(self):
        super(Policy, self).__init__()
        self.data = [] # 存储轨迹
        # 输入为长度为4的向量，输出为左、右2个动作，指定W张量的初始化方案
        self.fc1 = layers.Dense(128, kernel_initializer='he_normal')
        self.fc2 = layers.Dense(2, kernel_initializer='he_normal')
        # 网络优化器
        self.optimizer = optimizers.Adam(lr=learning_rate)

    def call(self, inputs, training=None):
        # 状态输入s的shape为向量：[4]
        x = tf.nn.relu(self.fc1(inputs))
        x = tf.nn.softmax(self.fc2(x), axis=1)  # 获得动作的概率分布
        return x

    def put_data(self, item):
        # 记录r,log_P(a|s)
        self.data.append(item)

    def train_net(self, tape):
        # 计算梯度并更新策略网络参数。tape为梯度记录器
        R = 0  # 终结状态的初始回报为0
        for r, log_prob in self.data[::-1]:  # 逆序取轨迹数据
            R = r + gamma * R  # 累加计算每个时间戳上的回报
            # 每个时间戳都计算一次梯度
            # grad_R=-log_P*R*grad_theta
            loss = -log_prob * R
            with tape.stop_recording():
                # 优化策略网络
                grads = tape.gradient(loss, self.trainable_variables)
                # print(grads)
                self.optimizer.apply_gradients(zip(grads, self.trainable_variables))
        self.data = []  # 清空轨迹


def main():
    pi = Policy()  # 创建策略网络
    pi(tf.random.normal((4, 4)))
    pi.summary()
    score = 0.0  # 计分
    print_interval = 20  # 打印间隔
    returns = []

    for n_epi in range(400):
        s = env.reset()  # 回到游戏初始状态，返回s0
        with tf.GradientTape(persistent=True) as tape:
            for t in range(501):  # CartPole-v1 forced to terminates at 500 step.
                # 送入状态向量，获取策略
                s = tf.constant(s, dtype=tf.float32)
                # s: [4] => [1,4]
                s = tf.expand_dims(s, axis=0)
                prob = pi(s)  # 动作分布:[1,2]
                # 从类别分布中采样1个动作, shape: [1]
                a = tf.random.categorical(tf.math.log(prob), 1)[0]
                a = int(a)  # Tensor转数字
                s_prime, r, done, info = env.step(a)
                # 记录动作a和动作产生的奖励r
                # prob shape:[1,2]
                pi.put_data((r, tf.math.log(prob[0][a])))
                s = s_prime  # 刷新状态
                score += r  # 累积奖励

                if n_epi > 1000:
                    env.render()
                    # im = Image.fromarray(s)
                    # im.save("res/%d.jpg" % info['frames'][0])

                if done:  # 当前episode终止
                    break
            # episode终止后，训练一次网络
            pi.train_net(tape)
        del tape

        if n_epi % print_interval == 0 and n_epi != 0:
            returns.append(score/print_interval)
            print(f"# of episode :{n_epi}, avg score : {score/print_interval}")
            score = 0.0
    env.close()  # 关闭环境

    plt.plot(np.arange(len(returns))*print_interval, returns)
    plt.plot(np.arange(len(returns))*print_interval, returns, 's')
    plt.xlabel('Number of Rounds')  # 回合数
    plt.ylabel('Total Return')  # 总回报
    plt.savefig('reinforce-tf-cartpole.svg')
    plt.show()


if __name__ == '__main__':
    main()