图神经网络(一)图信号处理与图卷积神经网络(2)图信号与图的拉普拉斯矩阵
给定图 G = ( V , E ) G=(V,E) G=(V,E),V表示图中的节点集合,假设其长度为 N N N,图信号是一种描述 V → R V→R V→R的映射,表示成向量的形式: x = [ x 1 , x 2 , … , x N ] T x=[x_1,x_2,…,x_N]^{\rm T} x=[x1,x2,…,xN]T,其中 x i x_i xi表示的是节点 v i v_i vi上的信号强度,如图1-1所示,其中竖线长度表示节点上信号值的大小:
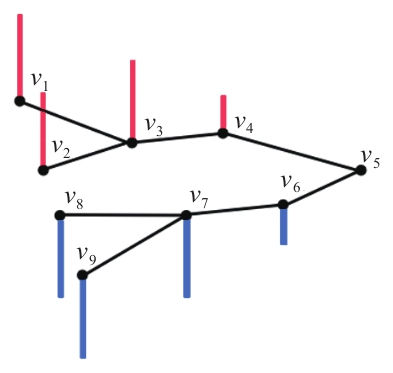
与离散时间信号不同,图信号是定义在节点上的信号,而节点之间有自己固有的关联结构。在研究图信号性质的时候,处理要考虑图信号的强度之外,还需要考虑图的拓扑结构,不同图上同一强度的信号,具有截然不同的性质。
拉普拉斯矩阵(Laplacian Matrix)是用来研究图的结构性质的核心对象,拉普拉斯矩阵的定义如下: L = D − A L=D-A L=D−A, D D D是一个对角矩阵, D i i = ∑ j A i j D_{ii}=∑_jA_{ij} Dii=∑jAij表示的是节点 v i v_i vi的度。拉普拉斯矩阵的元素级别定义如下:
L i j = { d e g ( v i ) if I = j − 1 if e i j ∈ E 0 otherwise L_{ij}=\begin{cases} deg(v_i) &\text{if}\quad I=j\\ -1 &\text{if}\quad e_{ij}\in E\\ 0 &\text{otherwise} \end{cases} Lij=⎩⎪⎨⎪⎧deg(vi)−10ifI=jifeij∈Eotherwise
拉普拉斯矩阵还有一种正则化的形式(symmetric normalized laplacian) L sym = D − 1 / 2 L D − 1 / 2 L_{\text{sym}}=D^{-1/2} LD^{-1/2} Lsym=D−1/2LD−1/2,元素级别定义如下:
L sym = { 1 if I = j − 1 ( d e g ( v i ) d e g ( v j ) if e i j ∈ E 0 otherwise L_{\text{sym}}=\begin{cases} 1&\text{if}\quad I=j\\ \frac{-1}{\sqrt{(deg(v_i )deg(v_j )}}&\text{if}\quad e_{ij}\in E\\ 0 &\text{otherwise} \end{cases} Lsym=⎩⎪⎪⎨⎪⎪⎧1(deg(vi)deg(vj)−10ifI=jifeij∈Eotherwise
拉普拉斯矩阵的定义来源于拉普拉斯算子,拉普拉斯算子是 n n n维欧式空间中的一个二维微分算子: ∆ f = ∑ i = 1 n ∂ 2 f ∂ x i 2 ∆f=∑_{i=1}^n\frac{∂^2f}{∂x_i^2} ∆f=∑i=1n∂xi2∂2f 。如果将该算子的作用域退化到离散的二维图像空间,就成了我们非常熟悉的边缘检测算子,其作用原理如下:
∆ f ( x , y ) = ∂ 2 f ( x , y ) ∂ x 2 + ∂ 2 f ( x , y ) ∂ y 2 = [ ( f ( x + 1 , y ) − f ( x , y ) ) − ( f ( x , y ) − f ( x − 1 , y ) ) ] + [ ( f ( x , y + 1 ) − f ( x , y ) ) − ( f ( x , y ) − f ( x , y − 1 ) ) ] = [ ( f ( x + 1 , y ) + f ( x − 1 , y ) ) + ( f ( x , y + 1 ) − f ( x , y − 1 ) ) ] − 4 f ( x , y ) \begin{aligned}∆f(x,y)&=\frac{∂^2 f(x,y)}{∂x^2} +\frac{∂^2f(x,y)}{∂y}^2\\ &=[(f(x+1,y)-f(x,y))-(f(x,y)-f(x-1,y))] +[(f(x,y+1)-f(x,y))-(f(x,y)-f(x,y-1))]\\ &=[(f(x+1,y)+f(x-1,y))+(f(x,y+1)-f(x,y-1))]-4f(x,y)\end{aligned} ∆f(x,y)=∂x2∂2f(x,y)+∂y∂2f(x,y)2=[(f(x+1,y)−f(x,y))−(f(x,y)−f(x−1,y))]+[(f(x,y+1)−f(x,y))−(f(x,y)−f(x,y−1))]=[(f(x+1,y)+f(x−1,y))+(f(x,y+1)−f(x,y−1))]−4f(x,y)
在处理图像的时候,上式中的算子会被表示成模板的形式:
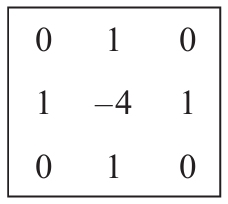
从模板中我们可以直观地看到,拉普拉斯算子也被用来描述中心节点与邻居节点之间的信号的差异。
同理,在图信号中,拉普拉斯算子也被用来描述中心节点与邻居节点之间的信号差异,这从下式中可以看出:
L x = ( D − A ) x = [ ⋯ , ∑ v j ∈ N ( v j ) , ⋯ ] L\boldsymbol x=(D-A)\boldsymbol x=[\dotsb, \sum_{v_j\in N(v_j)}, \dotsb] Lx=(D−A)x=[⋯,vj∈N(vj)∑,⋯]
由此可知,拉普拉斯矩阵是一个反映图信号局部平滑度的算子。更进一步来说,拉普拉斯矩阵可以让我们定义一个非常重要的二次型:
x T L x = ∑ v i ∑ v j ∈ N ( v i ) x i ( x i − x j ) = ∑ e i j ∈ E ( x i − x j ) 2 \boldsymbol x^\text{T}L\boldsymbol x=∑_{v_i}∑_{v_j∈N(v_i)}x_i(x_i-x_j )=∑_{e_{ij}∈E}(x_i-x_j )^2 xTLx=vi∑vj∈N(vi)∑xi(xi−xj)=eij∈E∑(xi−xj)2
令 T V ( x ) = x T L x = ∑ e i j ∈ E ( x i − x j ) 2 TV(\boldsymbol x)=\boldsymbol x^\text{T} L\boldsymbol x=∑_{e_{ij}∈E}(x_i-x_j)^2 TV(x)=xTLx=∑eij∈E(xi−xj)2,我们称 T V ( x ) TV(\boldsymbol x) TV(x)为图信号的总变差(Total Variation)。总变差是一个标量,它将各条边上信号的差值进行加和,刻画了图信号整体的平滑度。
参考文献
[1] 刘忠雨, 李彦霖, 周洋.《深入浅出图神经网络: GNN原理解析》.机械工业出版社.