持续创作,加速成长!这是我参与「掘金日新计划 · 6 月更文挑战」的第11天,点击查看活动详情
在给定观测序列的条件下,找到可以使观测序列出现概率最大的状态序列,也就是在观测序列和参数是已知条件下,找到一个让后验概率
P(I∣O,λ) 最大的状态序列
I
I^=IargmaxP(I∣O,λ)O={o1,o2,⋯,oT}
解码问题和预测问题
在给定观测序列的条件下,找到可以使观测序列出现概率最大的状态序列
P(i1,i2,⋯,iT∣o1,o2,⋯,oT)=P(o1,o2,⋯,oT)P(i1,i2,⋯,iT∣o1,o2,⋯,oT)
动态规划
我们将将求概率最大的问题转换为距离最短的问题,所以这里用动态规划来解决这个问题。这里要用算法就是一个比较基本动态规划算法,维特比(viterbi)算法。
δt(i)=i1,i2,⋯,it−1maxP(o1,o2,⋯,ot,i1,i2,⋯,it−1,it=qi)
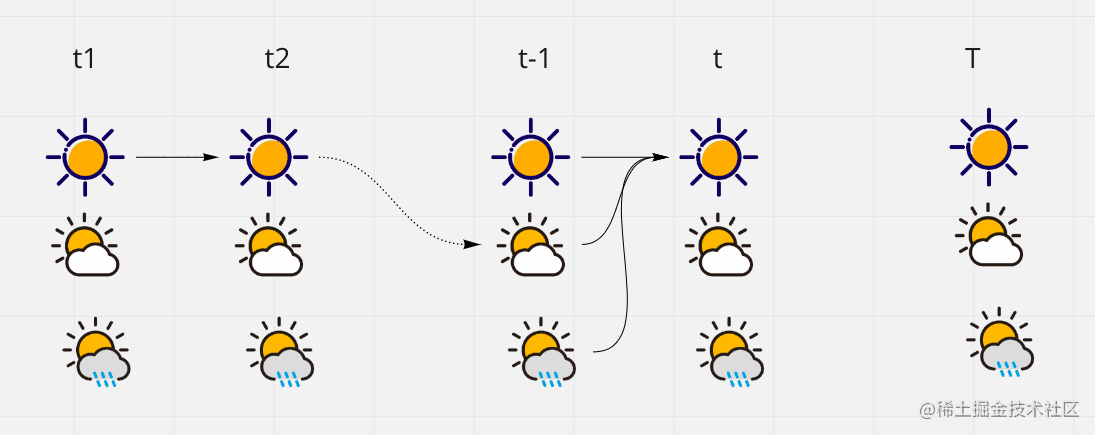
在 t 时刻到达
qi 状态的最大大概率的路径,
δt 就是表示最大值,上面公式因为
λ 是常数,所以就省略了。表示在 t 时刻前并不确定走那一条路径,只要在 t 时刻来到
qi 状态即可。从而这些排列组合可能路径中选择一条概率最大一条路径来将
δt 计算出来。
其实就是定义了局部状态,也就是在 t 时刻,当确定在 t 时刻状态为
qi 所有转移状态路径中概率最大路径,也就是局部状态,要找到路径所有可能性概率最大路径。也就是我们在 t 时刻知道其状态为
qi 我们是要找一条路径,这条路径到
qi 的概率最大。
φt(i)=1≤j≤Nargmax[δt(j)aji]
也就是上一个节点隐状态是什么,这里
φt−1(i) 是当我们已经找到了一条路径到当前时刻 t 状态为
qi 的概率最大路径,需要找到在这种情况下前一个时刻,也就是 t-1 时刻的状态是哪一个状态,这样好处是我们可以顺藤摸瓜找到 t 时刻概率最大所有对应一些列隐藏状态。
接下来根据
δt 定义来列出
θt+1(j) 当达到 t+1 时刻状态为
qj 让概率最大的路径,接下来工作就是找
δt 和
δt+1 之间的关系,也就是找到递推式
δt+1(j)=i1,⋯,itmaxP(o1,o2,⋯,ot,ot+1,i1,i2,⋯,it−1,it,it+1=qj)
maxδt(j)P(it+1=qj∣it=qi)P(ot+1∣it+1=qj)
aij=P(it+1=qj∣it=qi)bj(ot+1)=P(ot+1∣it+1=qj)
1≤i≤Nmaxδt(i)ajibj(ot+1)
也是也很好理解,也就是 j 是从 1 到 j 找到一个
δt 最大值然后乘以从 i 到 j 转移概率在乘以状态
qj 到
ot+1 的生成概率作为
δt+1(j) 的值
δt(i)=P(it=qi∣O,λ)
初始化
δ1(i)=πibi(o1)i=1,2,⋯,Nφ1(i)=0i=1,2,⋯,N
δt(i)=i≤j≤Nmax[δt−1(j)aji]bi(ot)φt(i)=i≤j≤Nargmax[δt−1(j)aji]
P∗=i≤j≤NmaxδT(i)
这里
p∗ 表示最可能出现隐藏状态序列出现概率,也就是让概率最大的隐含状态
iT∗=i≤j≤Nargmax[δT(i)]
在 T 时刻可以得到最可能隐藏状态,
it∗=φt+1(it+1∗) 根据
t+1 时刻发生概率最大隐状态
it+1∗ 就可以推出前一个时刻
t 时刻概率最大隐状态
it∗
实例
这里例子中,天气是状态,天气影响到 Bob 的心情,而这里观测变量是 Bob 的心情,然后在下图中列出状态转移概率和观测生成概率

为了便于计算表示我们将随机事件用具体数值表示,也就是随机变量的取值

观测序列如下,这就是我们观测 Bob 连续几天心情,由此我们来推测最近几天其所居住的城市天气状况

这里我们引入 numpy 来进行简单计算
import numpy as np
pi_0 = np.array([0.5,0.3,0.2])
A = np.array([
[0.6,0.2,0.2],
[0.5,0.3,0.2],
[0.6,0.2,0.2]
])
B = np.array([
[0.5,0.3,0.2],
[0.3,0.3,0.4]
])
复制代码
初始化
delta_1 = pi_0*B[0]
print(delta_1)
复制代码
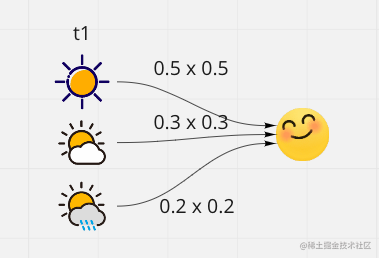
δ1(1)=π1b1(o1)=0.5×0.5=0.25δ1(1)=π1b1(o1)=0.3×0.3=0.09δ1(1)=π1b1(o1)=0.2×0.2=0.04
φ1(1)=φ1(2)=φ3(3)=0
迭代
δ2(1)=i≤j≤3max[δ1(j)aj1]b1(o2)=i≤j≤3max[0.25×0.6,0.09×0.5,0.04×0.6]×0.3=0.045δ2(2)=i≤j≤3max[δ1(j)aj1]b2(o2)=i≤j≤3max[0.25×0.2,0.09×0.3,0.04×0.2]×0.3=0.015δ2(3)=i≤j≤3max[δ1(j)aj1]b1(o2)=i≤j≤3max[0.25×0.2,0.09×0.2,0.04×0.2]×0.4=0.02
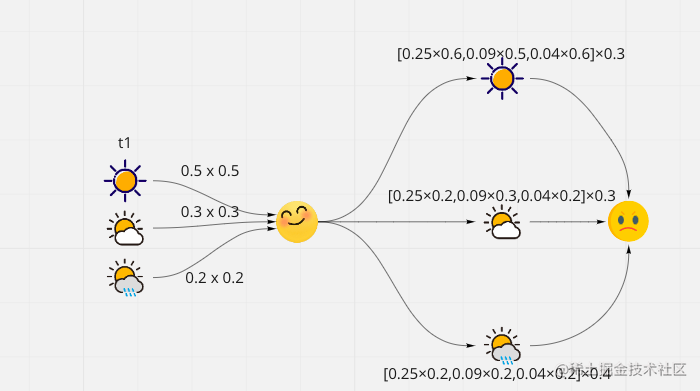
delta_2 = [ np.max(delta_1 * np.transpose(A)[idx]) for idx in range(3) ]*B[1]
print(delta_2)
复制代码
φ2(1)=1φ2(2)=1φ2(3)=1
print(np.argmax(delta_2))
复制代码
delta_3 = [ np.max(delta_2 * np.transpose(A)[idx]) for idx in range(3) ]*B[0]
print(delta_3)#[0.0135 0.0027 0.0018]
print(np.argmax(delta_3))#0
复制代码