卷积神经网络是最具代表性的深度学习算法之一,目前已经被大范围的应用与计算机视觉等领域,并且取得了众多突破性的进展,在学习卷积神经网络之前,我们需要学习图像卷积运算。
图像卷积运算的作用
图像卷积运算是一种图像处理算法。通过它可以实现很多不同的效果。例如,模糊图像中的细节。

提取图像中的边缘和轮廓。
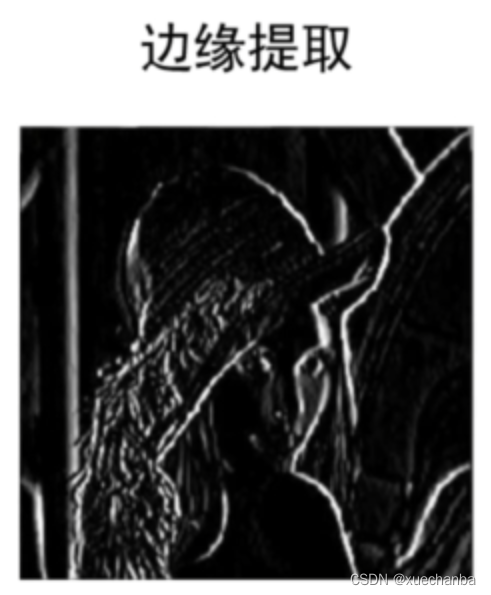
甚至把其变成浮雕效果。

那如何实现图像的卷积运算呢?
图像卷积运算的计算方法
数字图像在计算机中保存为一个矩阵,矩阵中每一个像素点的值就是图像中对应像素点的灰度值,对数字图像做卷积运算,
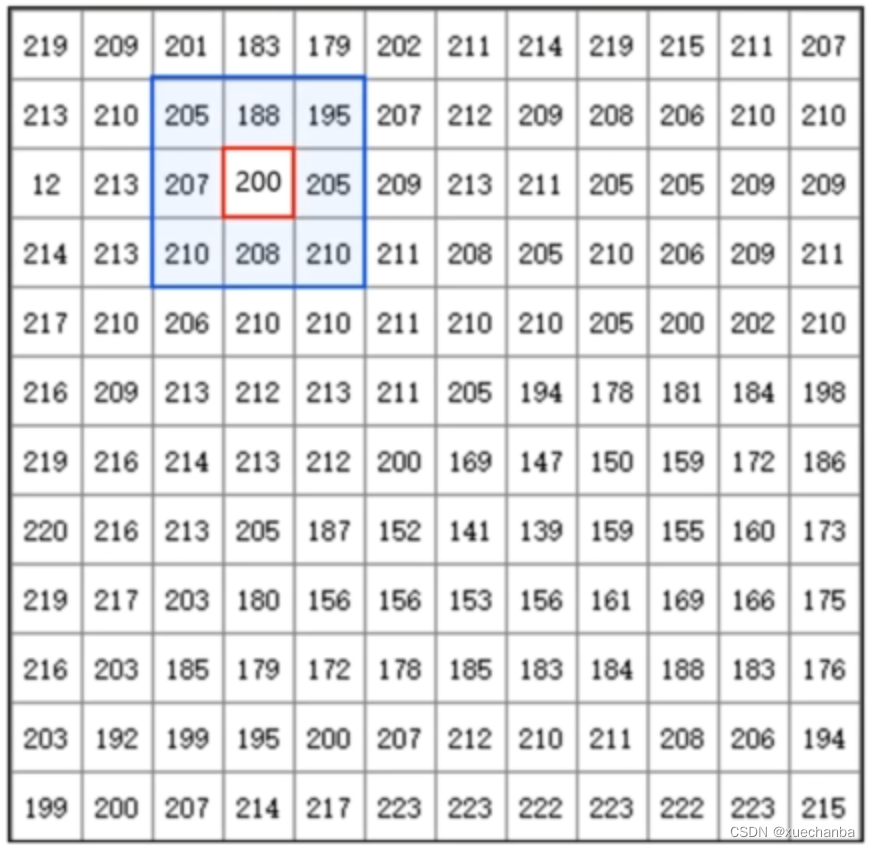
就是对图像中的每一个像素点,用它周围像素点的灰度值加权求和,从而调整这个点的灰度值。
首先,定义一个卷积核,卷积核也被称为卷积模板或卷积窗口。
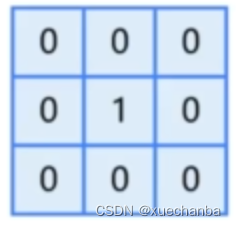
卷积核是一个 n x n 的矩阵,卷积核的尺寸决定了卷积运算的范围。它应该是一个奇数,这样才有一个中心点。卷积核中的数字就是这个点和它周围点的权值。
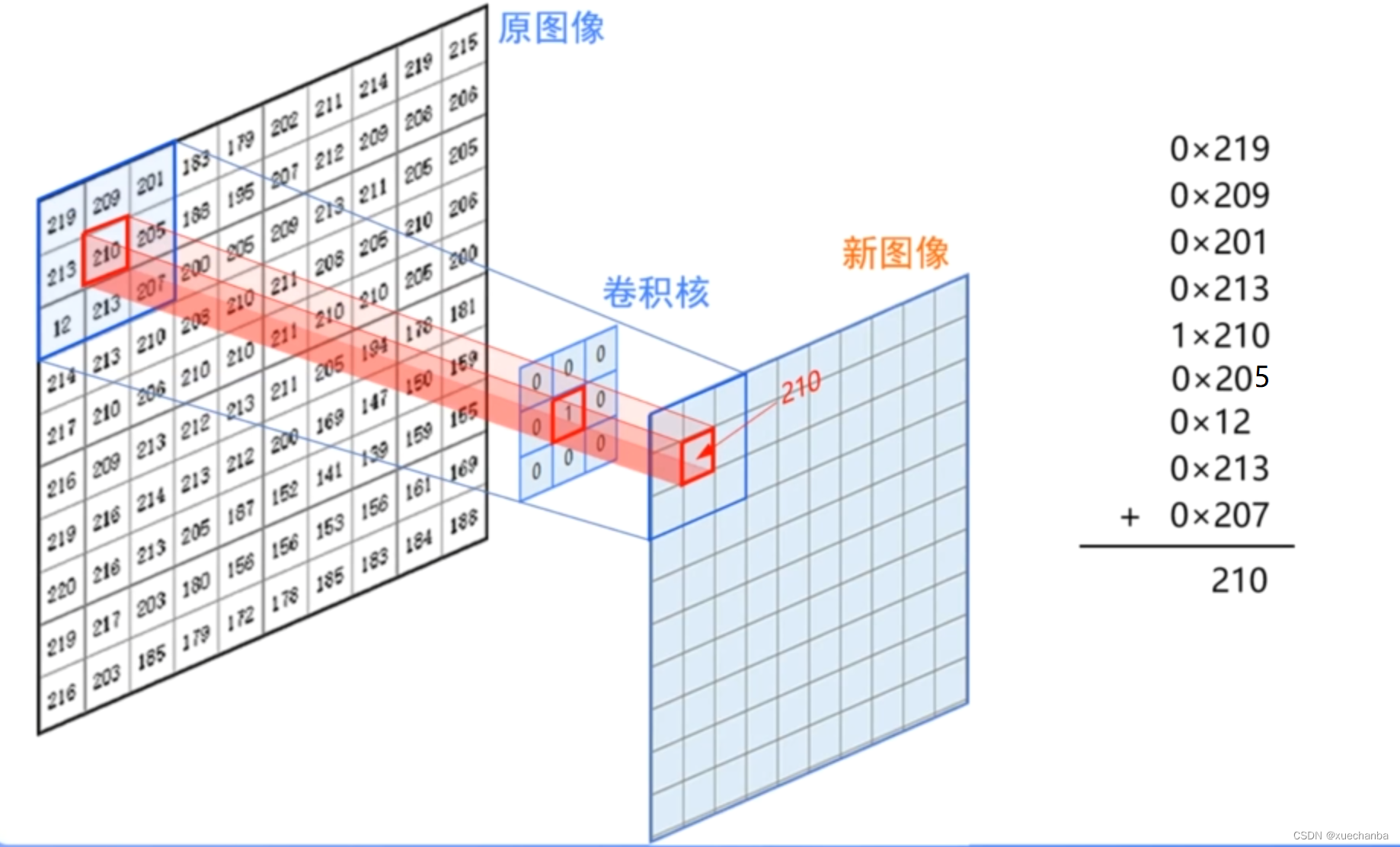
例如,在上图这个 3 x 3 的卷积核中,中心点的权值是 1 ,周围点的权值都是 0。
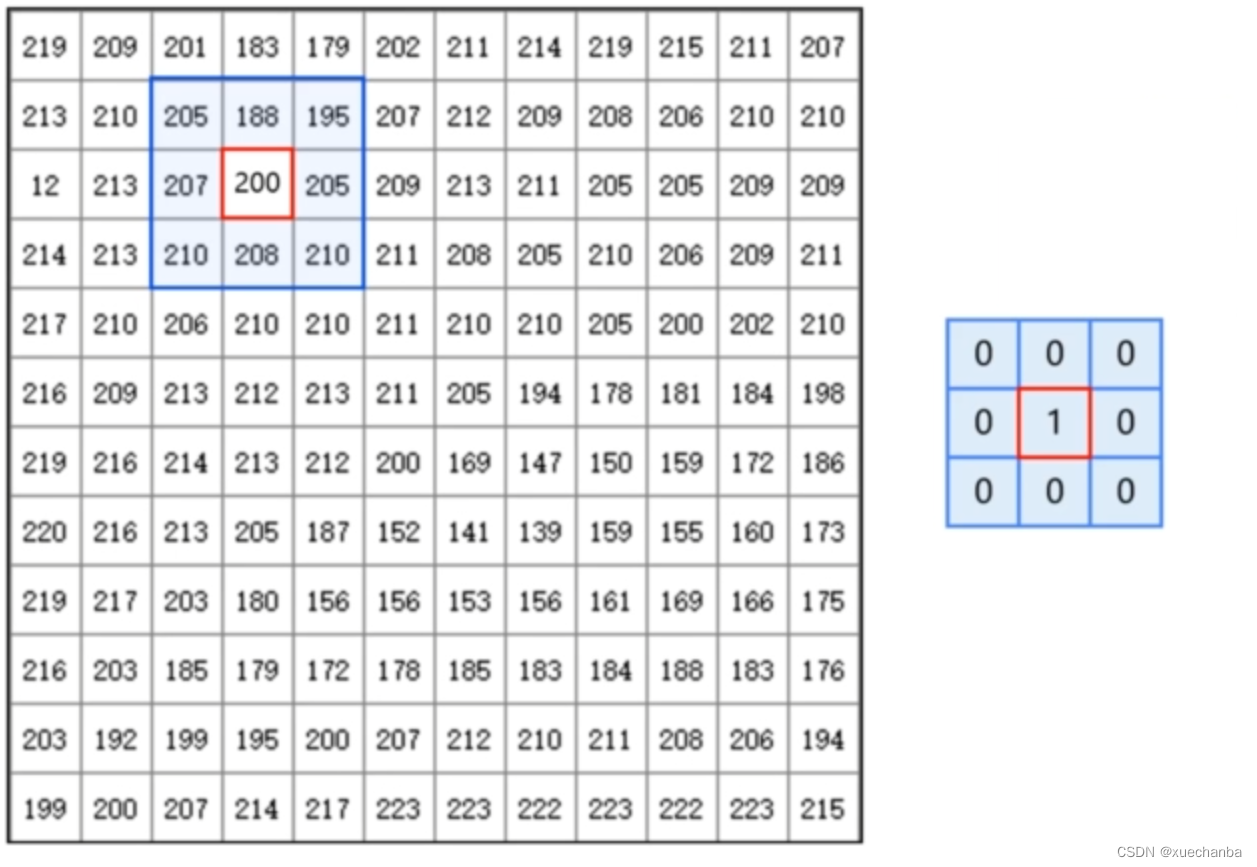
说明图像中这个中心点的灰度值不受周围像素点的影响。卷积运算之后的灰度值仍然是它本身。
下图为一个 5 x 5 的卷积核,
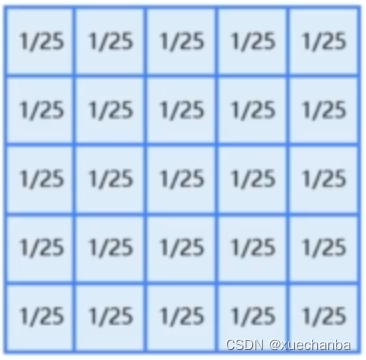
说明图像中每个点的像素值受到它周围两圈像素值的影响。
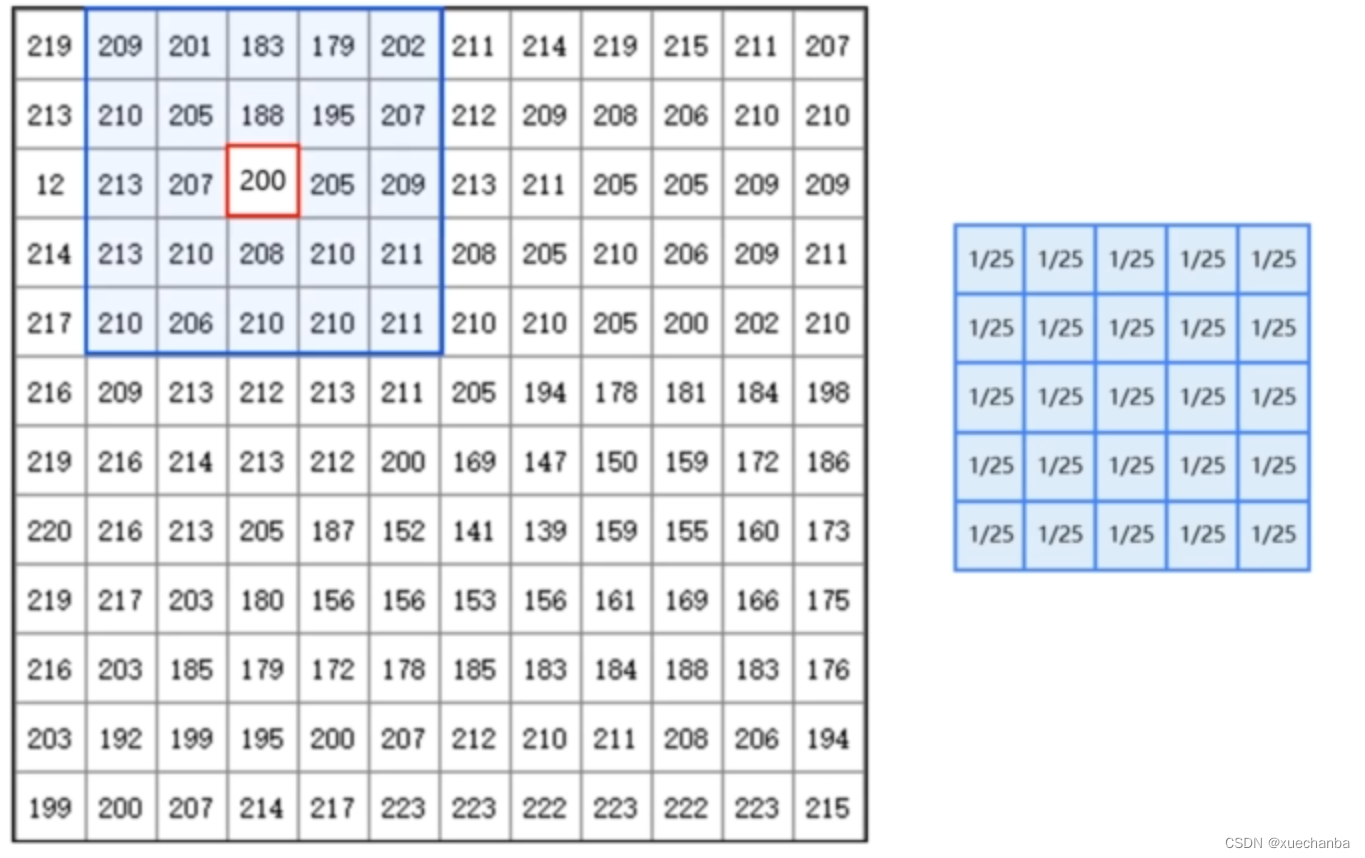
卷积核中所有的权值都是 1/25 , 表明所有点的贡献都一样。
图像的卷积运算需要多层嵌套实现,运算速度比较慢。因此,一般采用比较小的卷积核。例如,3x3、5x5 或者 7x7 的。
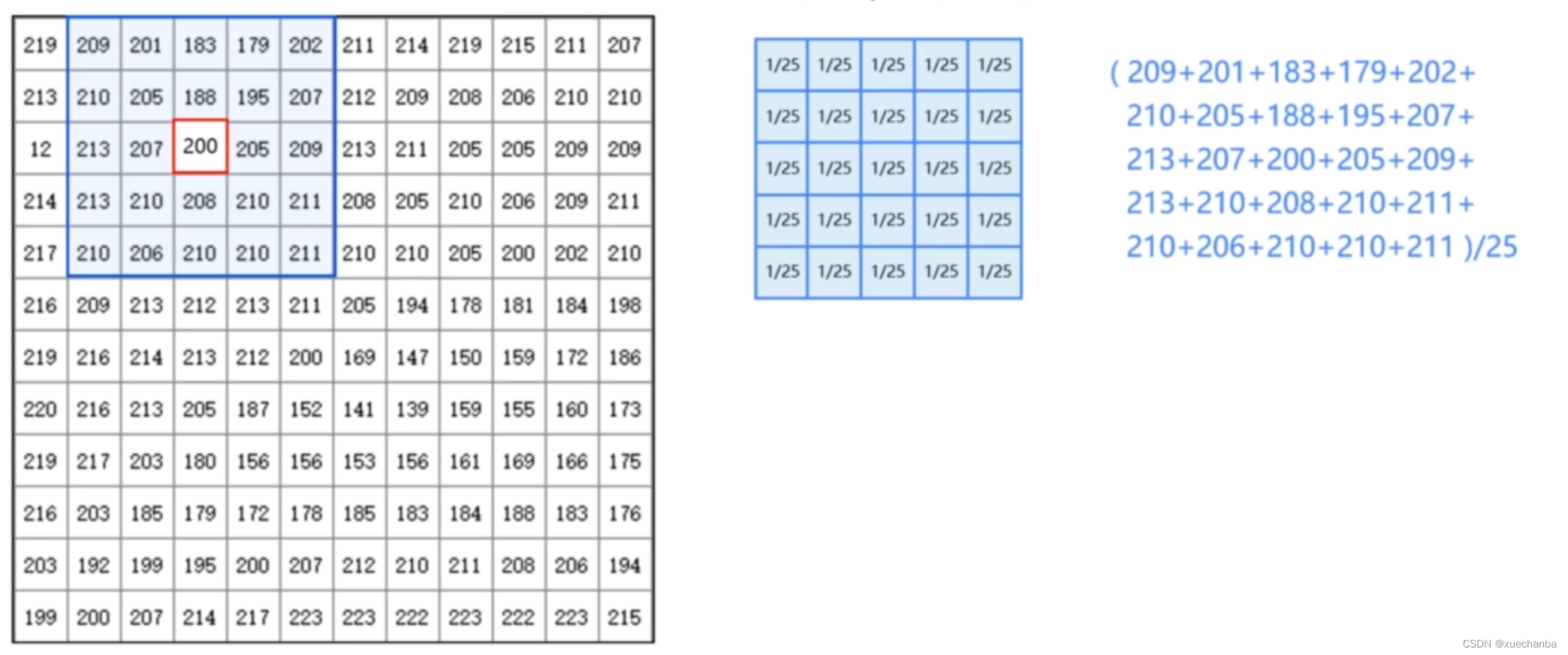
进行图像卷积运算时,首先要卷积核与图像中的像素点一一对应,然后加权求和。
接着把得到的结果作为中心像素点的新的灰度值。
然后将卷积核从左向右,从上到下滑动。

就可以依次计算出每个像素点的取值,完成对整个图像的卷积运算。
可以发现,使用 3 x 3 的卷积核,卷积运算得到的新图像会比原图像稍微小一些。例如,这里的 12 x 12 的原图像,使用 3 x 3 的卷积核,卷积之后的输出图像是 10 x 10 的。
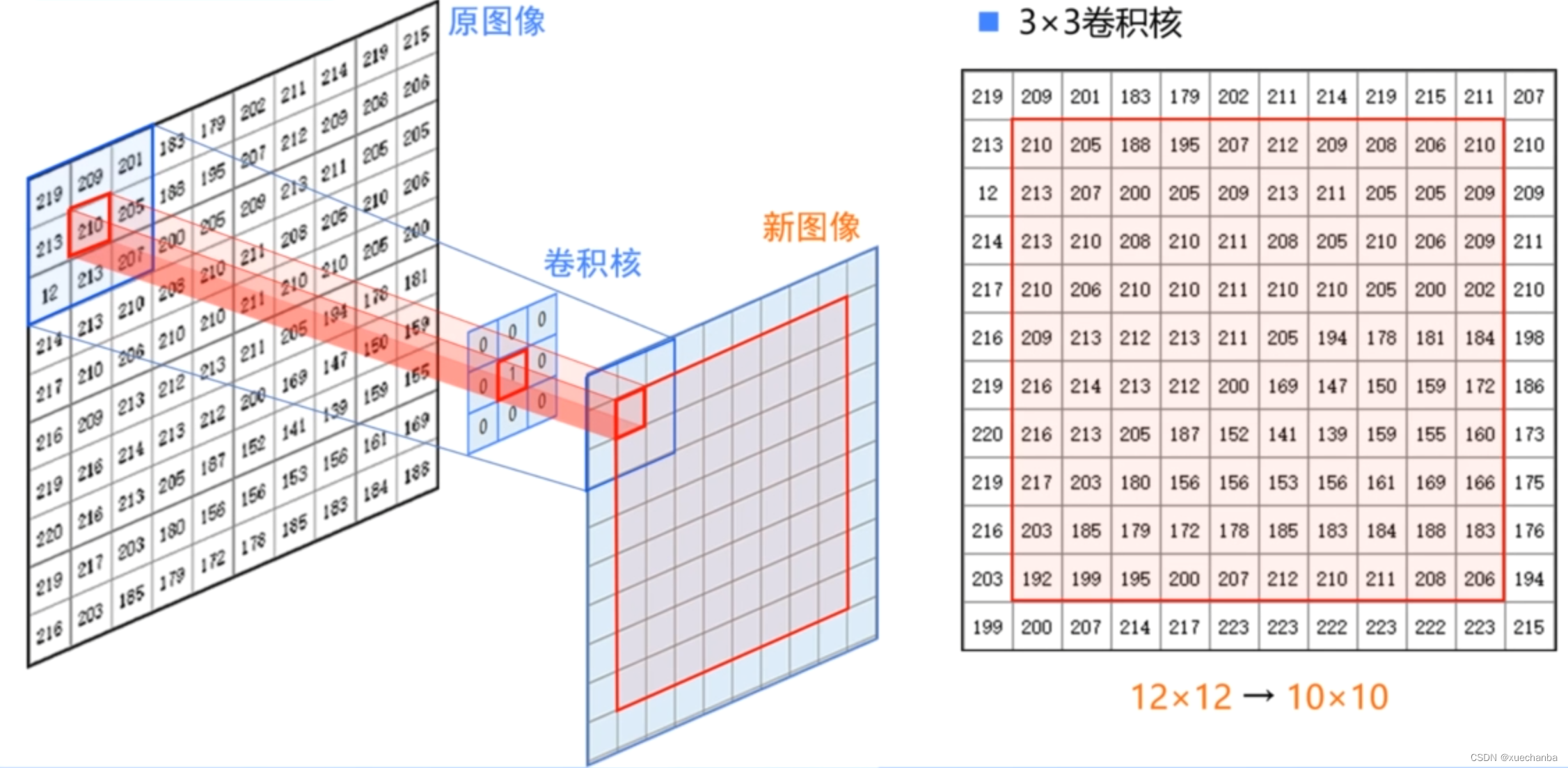
这是因为对于图像边界上的点,它们外面已经没有像素了,因此无法进行卷积运算。
使用 5 x 5 的卷积核时,最外面两层像素都无法进行卷积运算,得到的新图像会更小。
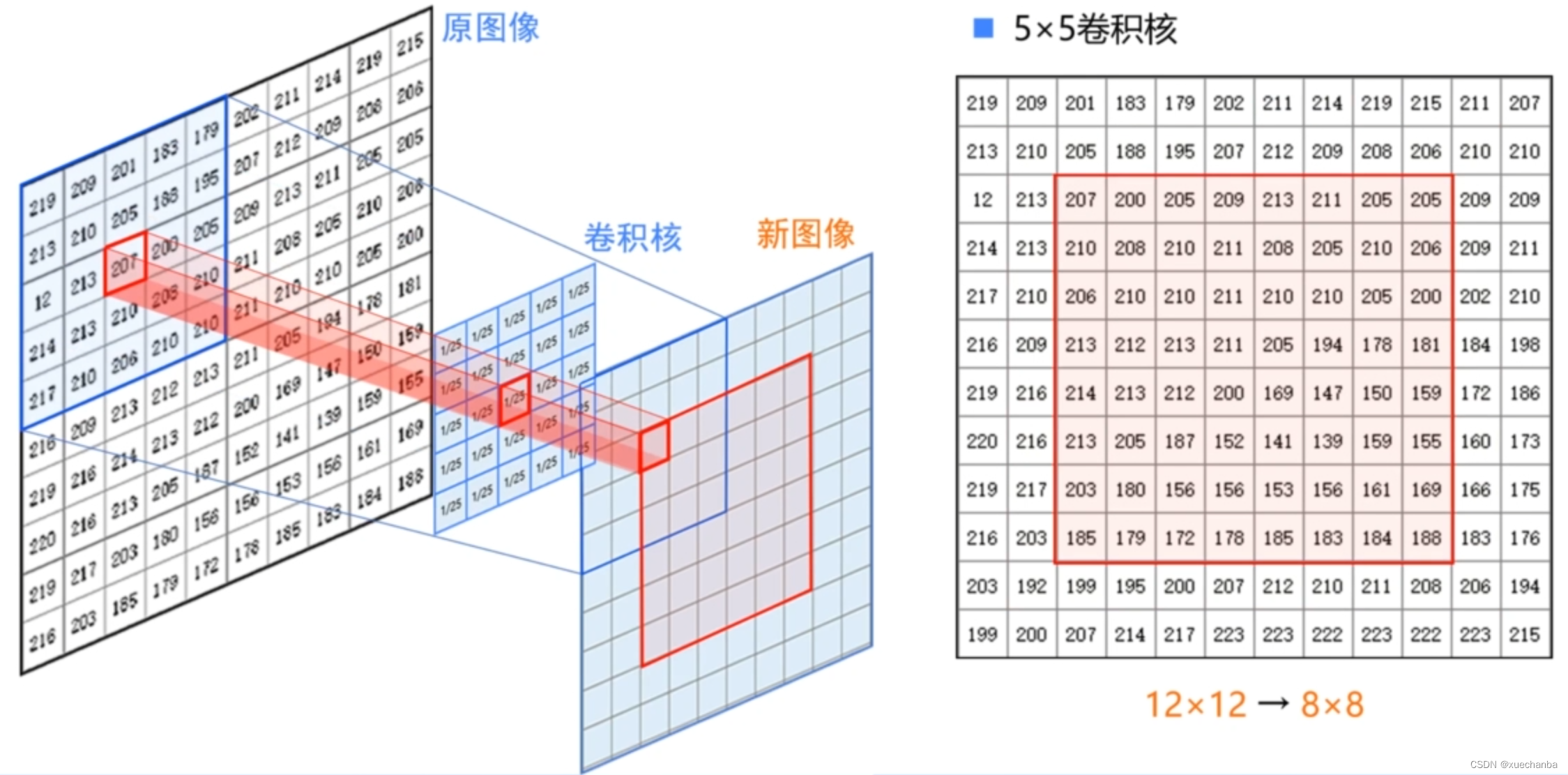
如果希望卷积运算得到的图像与原图的大小一致,可以在卷积运算之前,在图像周围填充一圈数字,如下图所示。
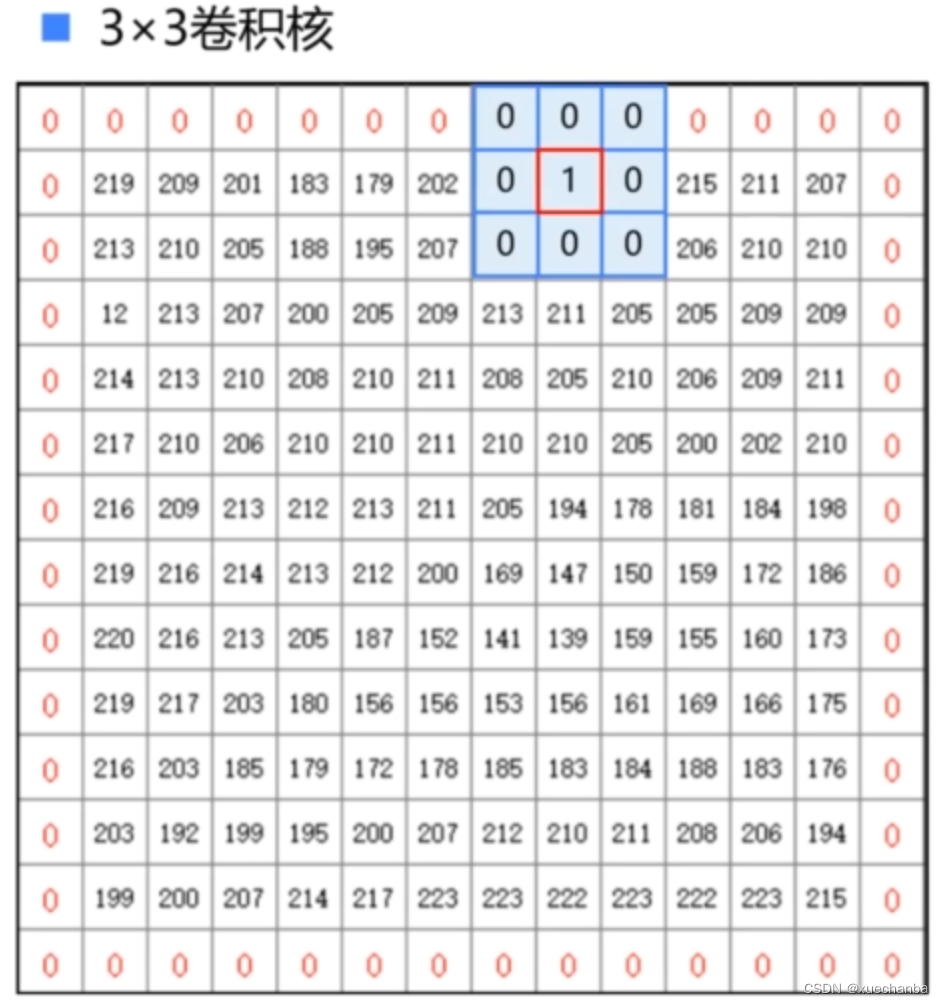
这样就可以计算图像边界处的卷积了。填充的数字不仅仅可以是0,还可以是 255 或者其他值。
例如,还可以将图像边界处的像素值直接向外延展,

如果使用 5 x 5 的卷积核,那么就需要向外填充两层。
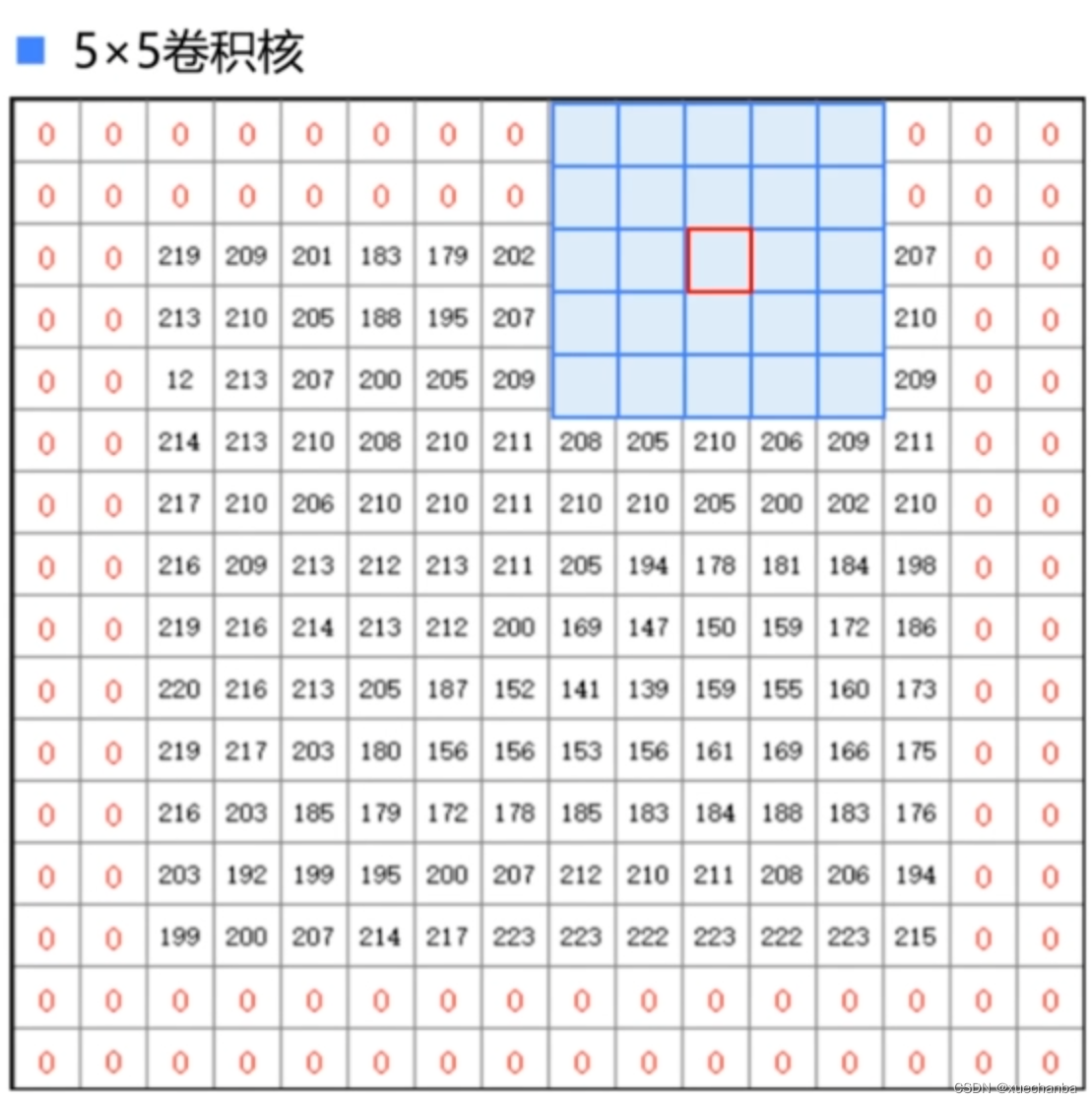
卷积核在从左向右、从上到下滑动的过程中,一次移动的像素数称为卷积运算的步长。在前面的例子中,水平和垂直方向滑动的步长都是1,当步长为 2 时,每次移动的卷积核会跳过 2 个像素点。
显然,这时的输出图像会变的更小。
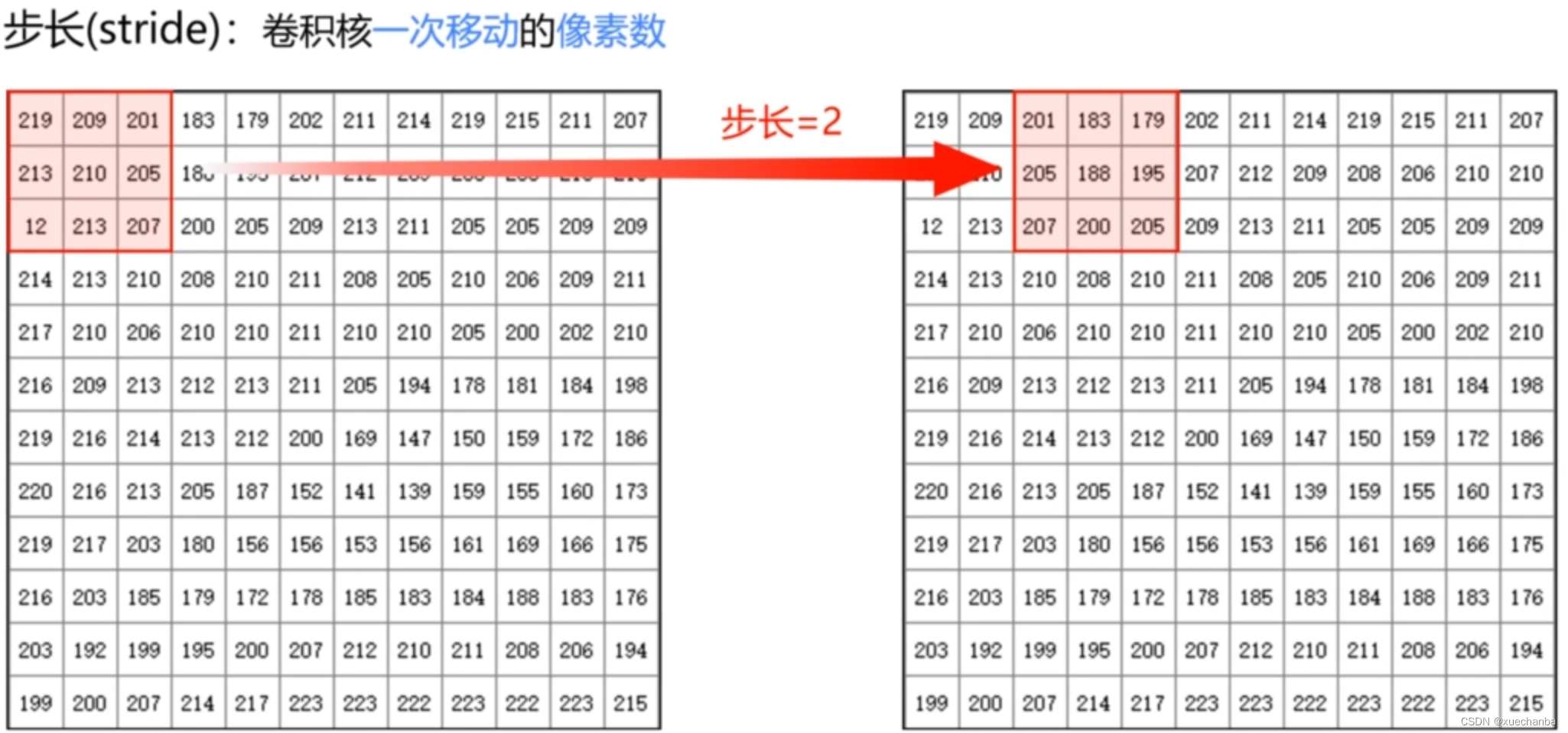
最极端的情况下,如果步长等于卷积核的边长 n ,那么就相当于对图像缩小了 n 倍。
例如,对于 12 x 12 的图像来说,使用 3 x 3 的卷积核,步长为 3 时,只能够计算下图中框出的这些像素的卷积。
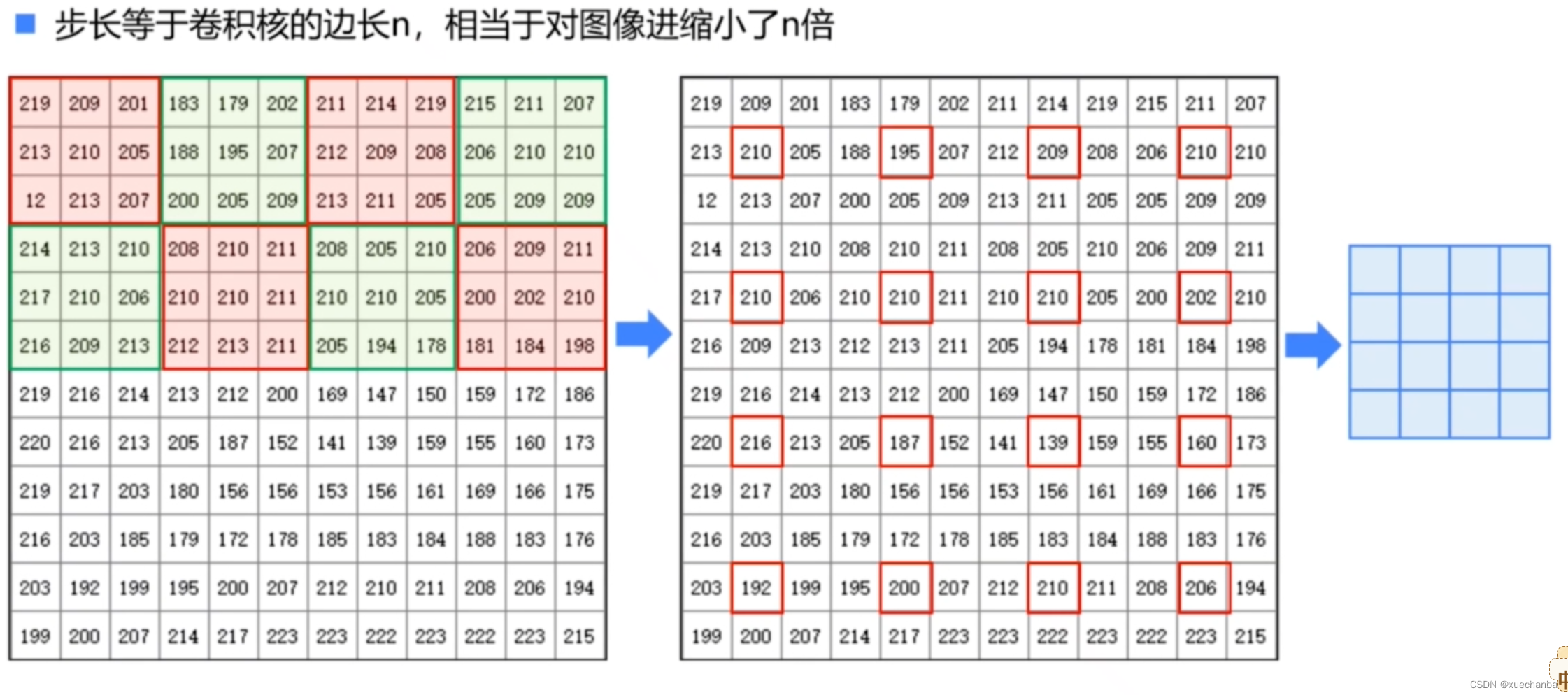
因此,输出的图片是 4 x 4 的。
要注意的是,在信号处理领域中,卷积有着严格的数学定义,并且有着更加广泛的意义。 在这门课中,我们只要了解图像卷积运算的方法即可。
图像卷积
输出原图
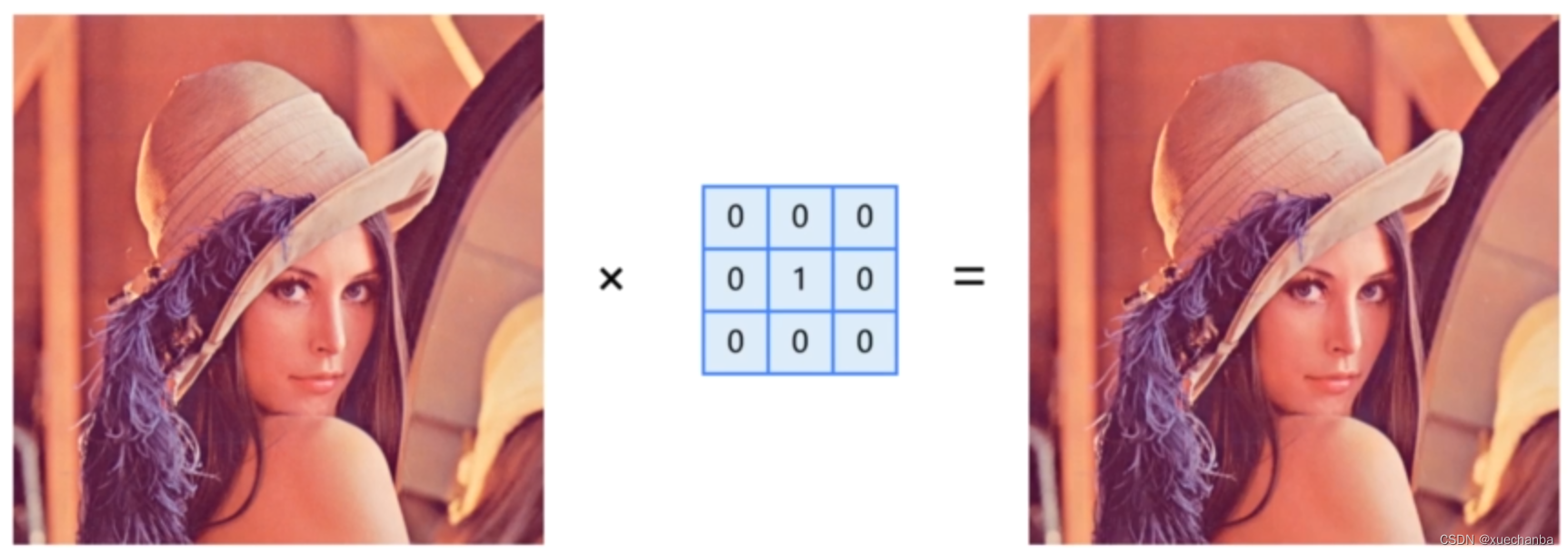
在下图中,卷积核采用 3 x 3 的卷积核,这个卷积核只有中心点的权值为 1 ,其余点都是 0,表面图像中每个像素点的取值不会受到周围像素点的影响,卷积运算输出的结果就是原图。
均值模糊
下图这个卷积核,
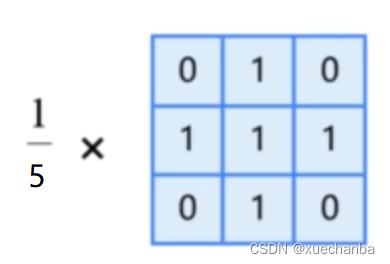
将当前像素和它上下左右相邻的四个像素点一起求平均值,称为 4 邻域平均法。它使得图像变的模糊,一般来说,卷积核中所有元素之和应该等于 1 ,因为这样经过卷积运算之后,图像的亮度保持不变。
下图这个卷积核,
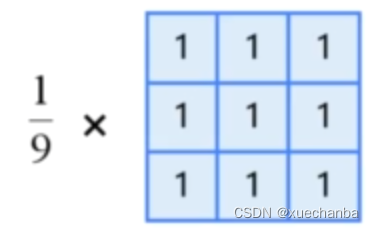
将当前像素和它相邻的八个像素点一起求平均值,称为 8 邻域平均法。它使得图像变的更模糊。
如果想要更强的模糊效果,可以加大卷积核的尺寸。下图为使用 5 x 5 的卷积核,均值模糊后的结果。
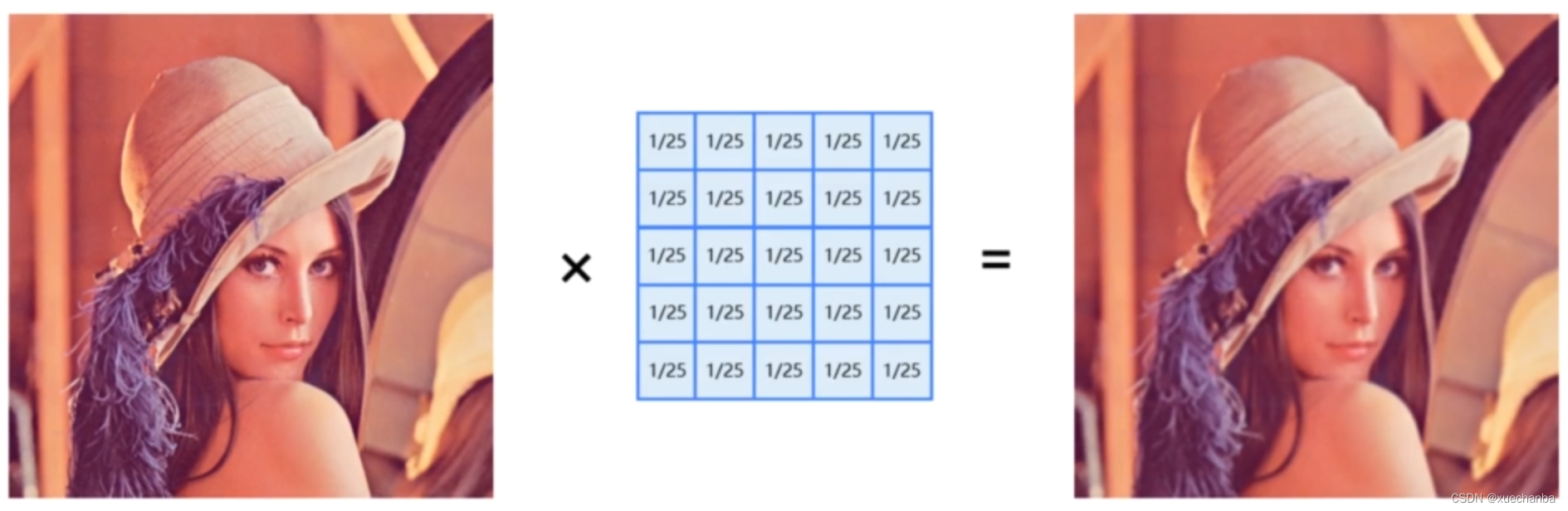
通过卷积运算,对图像进行模糊后,可以将图像中的高频噪声给过滤掉。因此,对图像的卷积运算也称为平滑或者滤波。卷积核也称为滤波器。
下图为对一张图片进行不同卷积核均值模糊后的结果。
 可以看到卷积核的尺寸越大,图像就越模糊。
可以看到卷积核的尺寸越大,图像就越模糊。
由于均值模糊是对窗口中所有像素点求平均值,在图像的边缘或者纹理丰富的地方也会变得模糊。为了尽可能的保留图像中的边缘信息,可以给不同位置的像素点赋以不同的权值。距离中心点越近的像素,权值越大,而远离中心点的像素,权值也逐渐减少。
高斯模糊

高斯分布就是正态分布,下图为一维高斯函数。
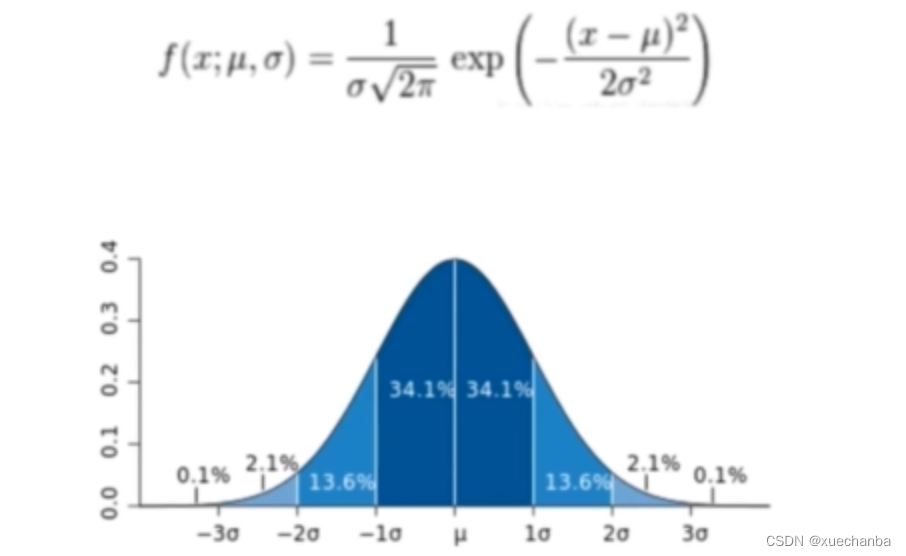
下图为二维高斯函数。
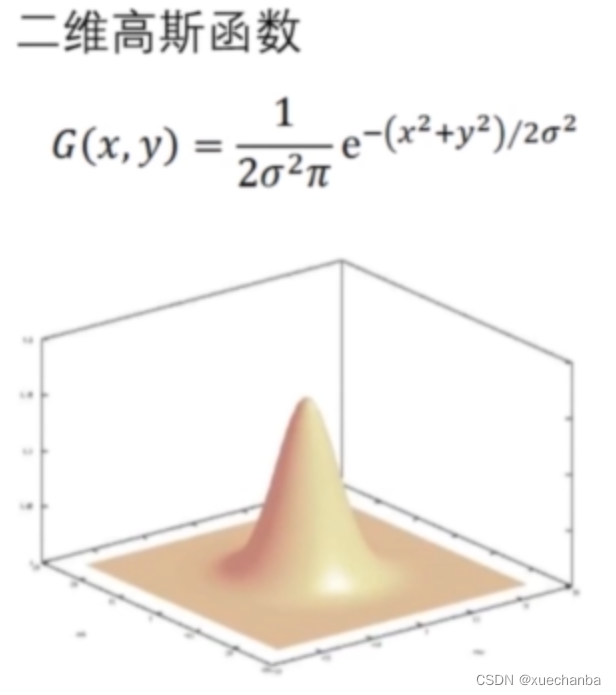
取二维高斯函数的值作为卷积核,
(详细操作过程可看该文章:https://blog.csdn.net/u013066730/article/details/123112159)
这是 3 x 3 的高斯卷积核,
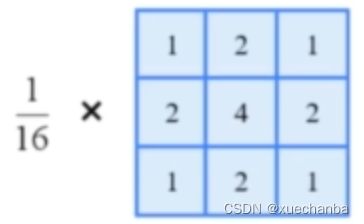
下图为 5 x 5 的高斯卷积核,
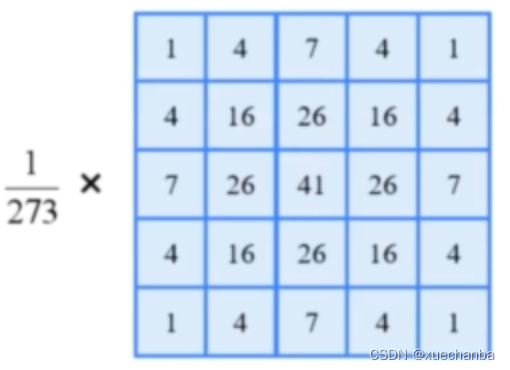
可以看到,距离中心越近,权值越大。
对于下图,是分别进行均值模糊和高斯模糊之后的结果。

可以看到,高斯模糊在平滑物体表面的同时,能够更好的保持图像的边缘和轮廓。
边缘检测
图像边缘是图像中颜色、灰度或者亮度发生极具变化的区域边界,是图像最基本的、也是最重要的特征之一。

边缘检测实质上是计算当前点和周围点灰度的差别。
例如,有这样一张图片,

这是其中每个像素点的灰度值,
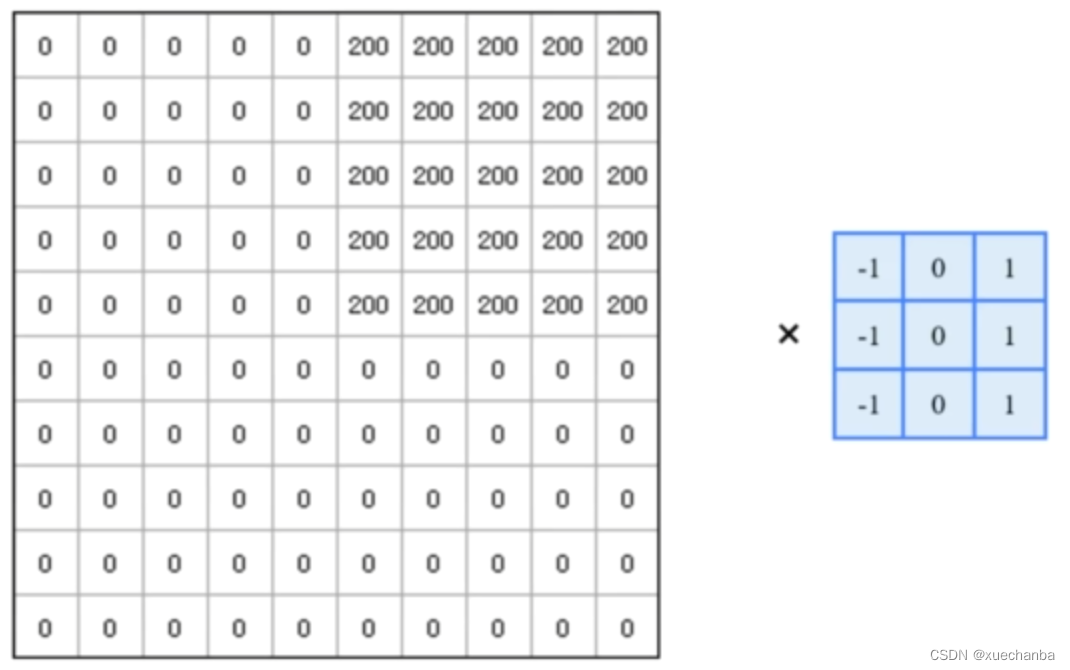
可以使用这样的卷积核来找到它的数值边缘。这个卷积核的作用就是用中心点右边的像素值减去其左边的像素值。
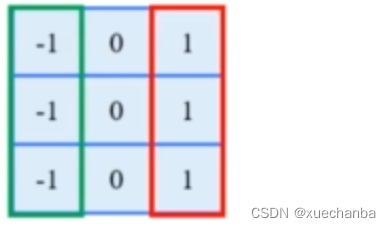
下图为卷积之后的结果。
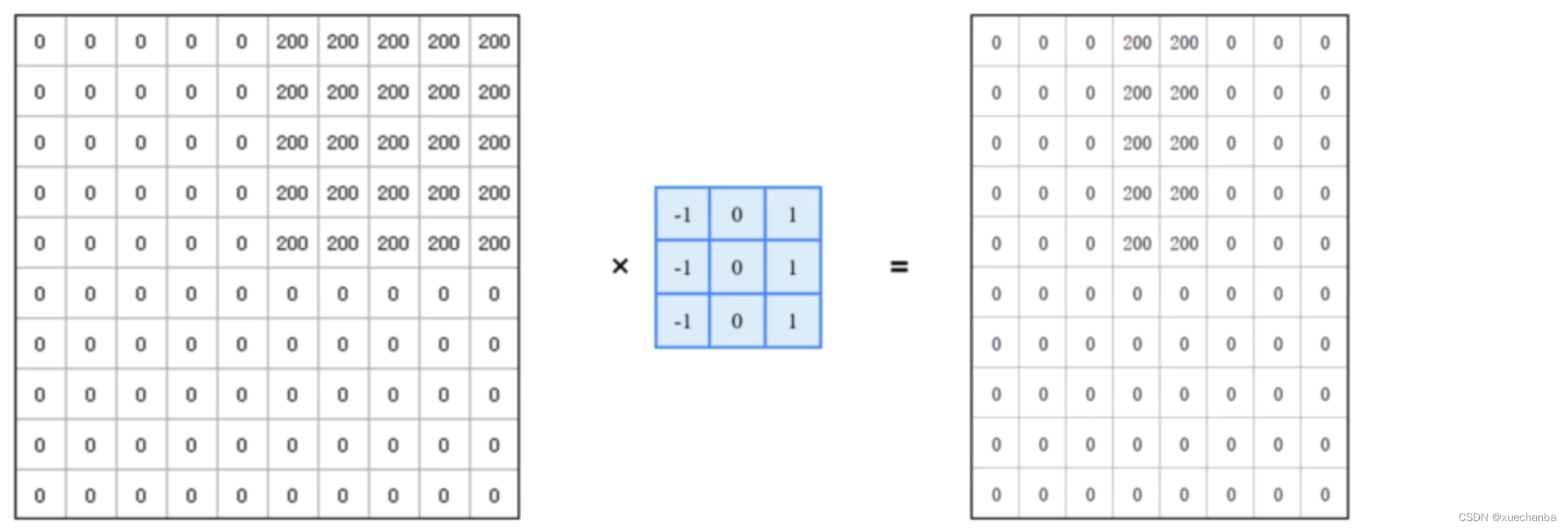
可以看到,如果左右两边的灰度值一样,那么差值等于 0 ,也就是黑色。而在图案的边缘,灰度值差距比较大 ,就会得到一个高亮度的区域,差值越大,亮度越高。
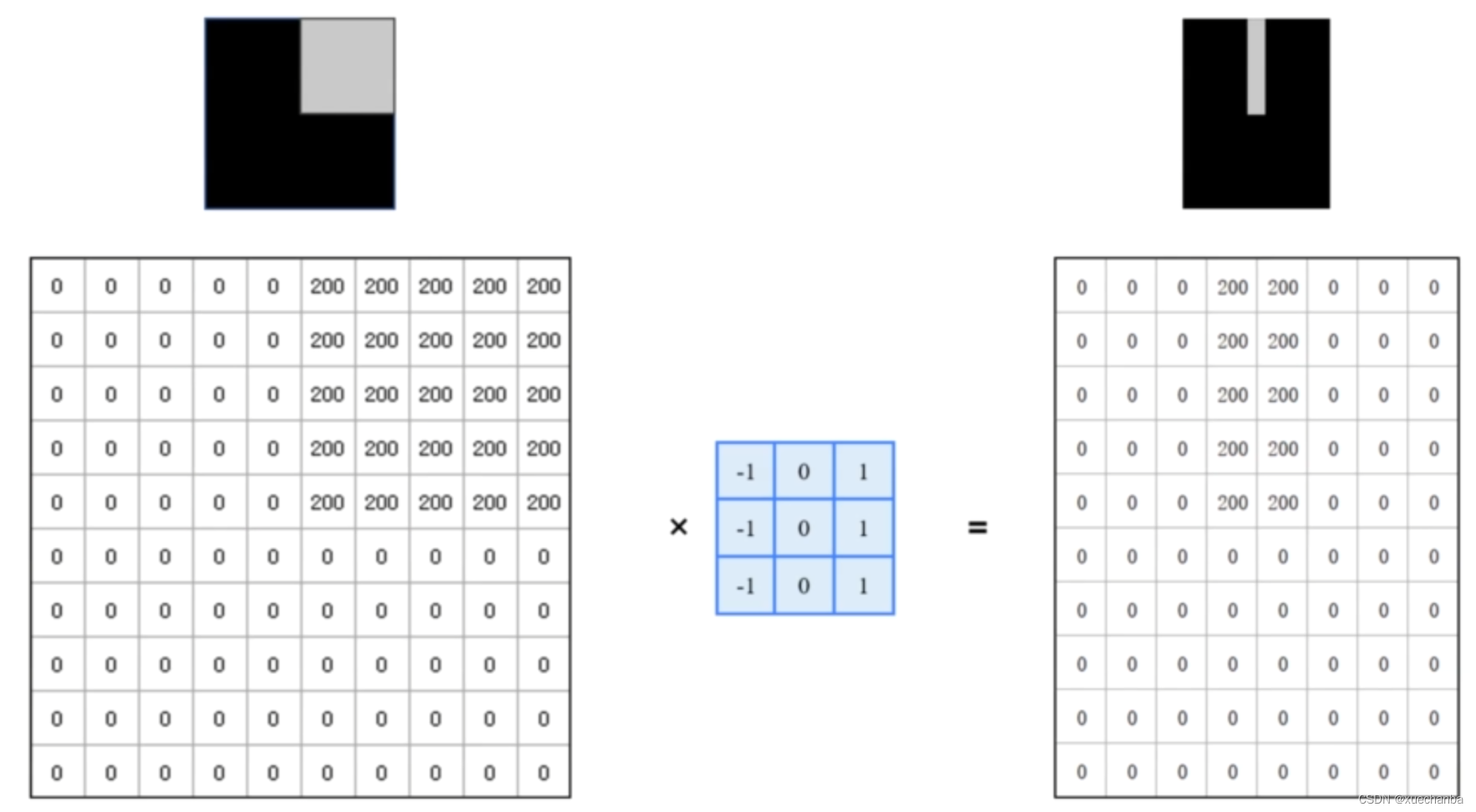
因此,通过这个卷积核就可以找到垂直的边缘。
在这个卷积核中,所有的权值之和等于 0 ,运算之后的图像整体很暗,只有边缘的地方是有亮度的。
如果要检测水平的边缘,可以使用下图这个卷积核。
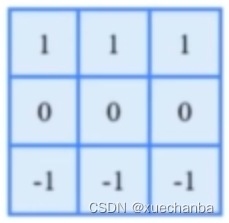
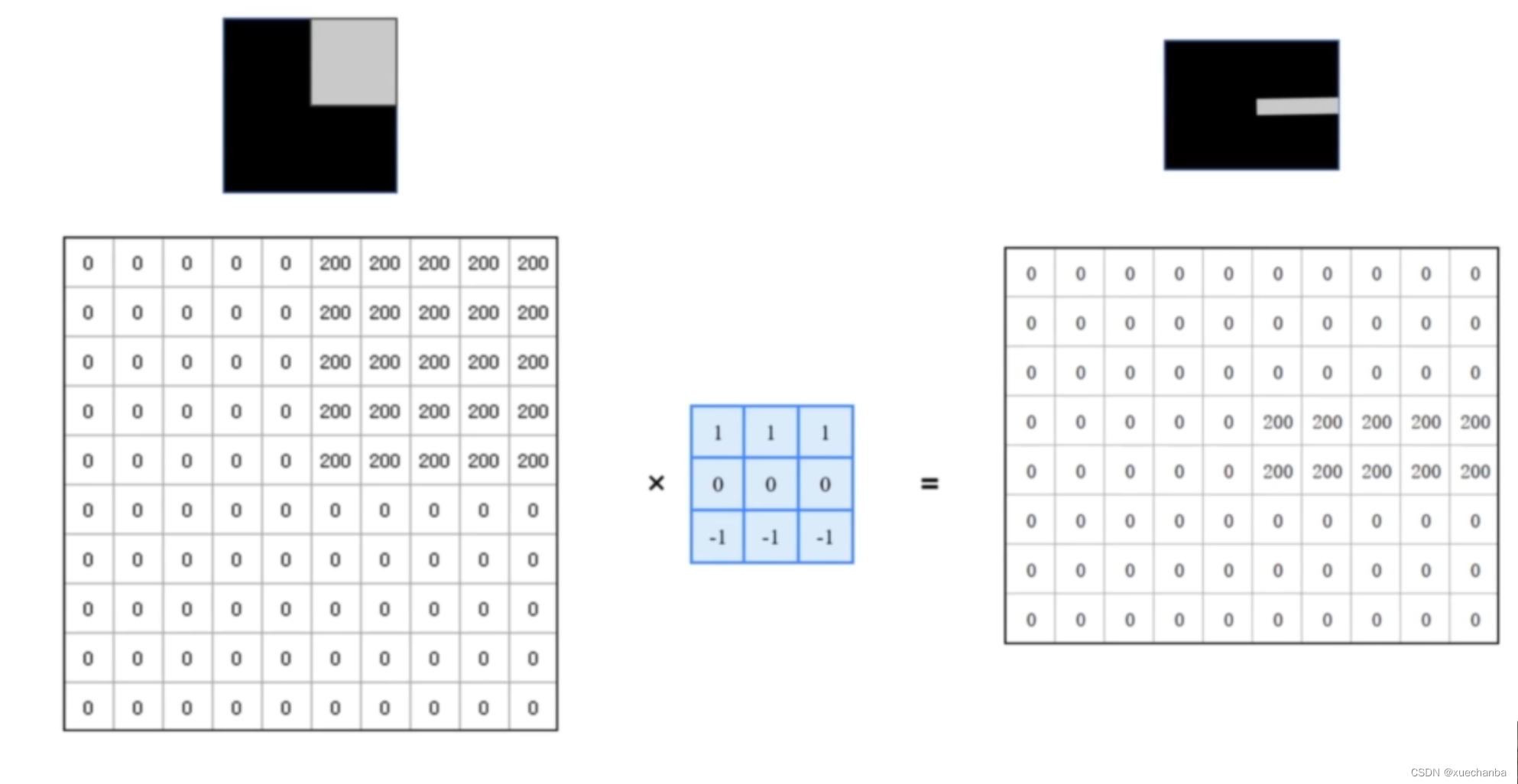
将以上两种卷积组合起来,就可以得到完整的边缘。这种卷积核被称为 Prewitt 算子。
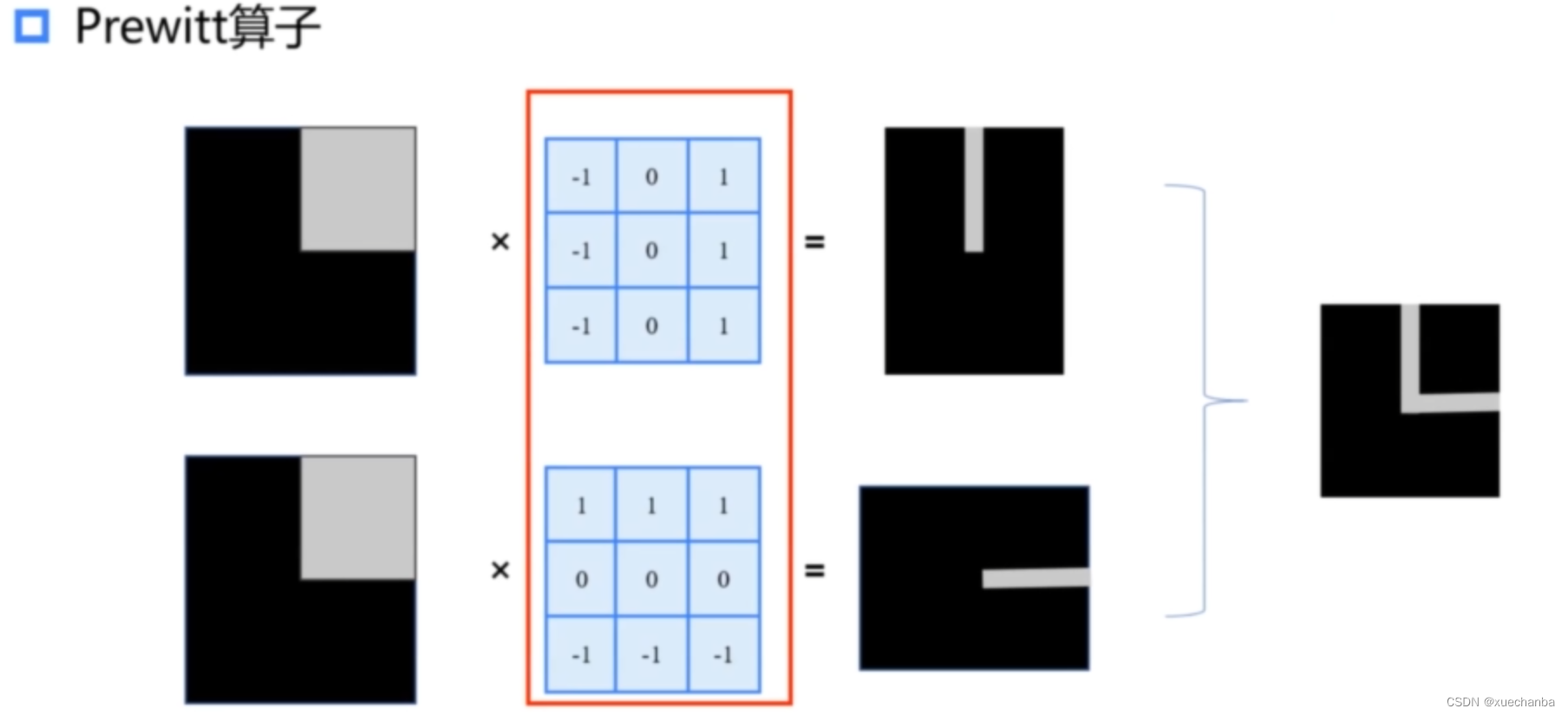
除此之外,还有其他一些边缘检测算子。
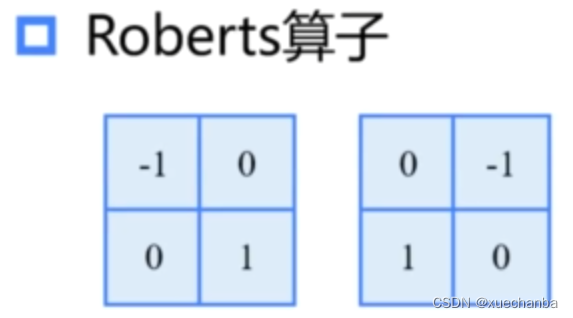
它能够比较好的检测到 45° 角方向的边缘。
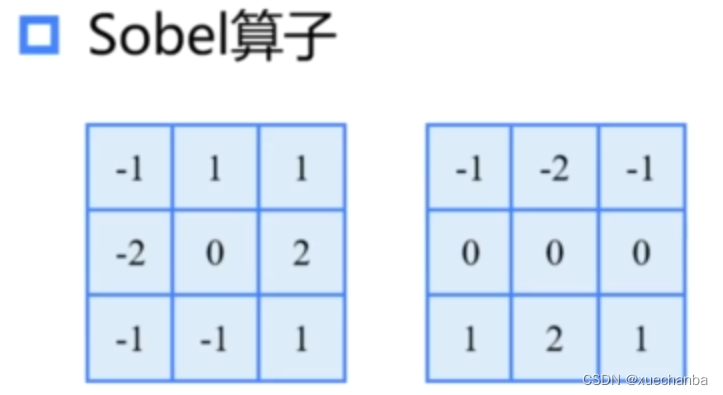
它在 Prewitt 算子的基础之上,增加了权重的概念,认为上下左右直线方向的距离大于斜线方向的距离。因此,它们(左右直线方向)的权值更大。
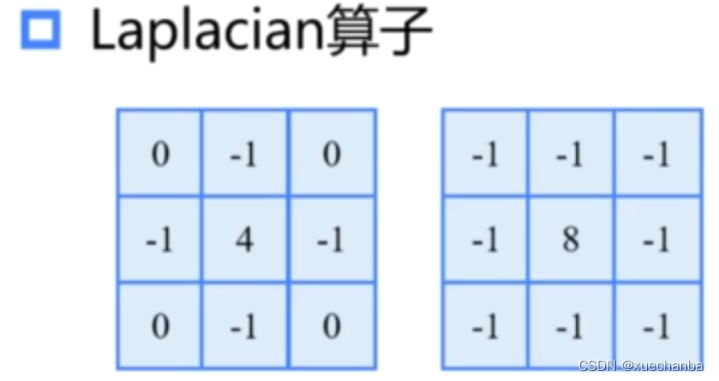
拉普拉斯算子,它通过对邻域中心像素的四方向或者八方向求梯度,再将梯度相加起来,从而判断中心像素灰度与邻域内其他像素灰度的关系。
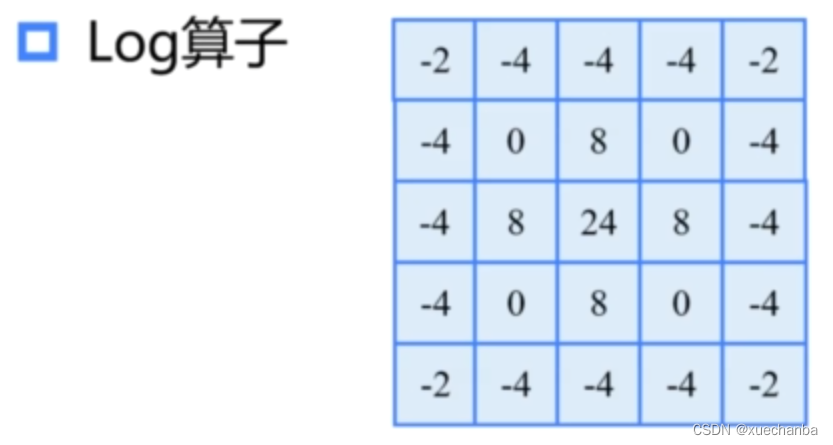
它将高斯和拉普拉斯算子相结合,综合考虑了对噪声的抑制和边缘检测,它的抗干扰能力强。边界定位精度高。边缘连续性也更好。而且能够有效提取对比度弱的边界。在图像处理领域中,得到了广泛的应用。
下图为对 Lena 图像使用不同的边缘检测算子得到的结果。
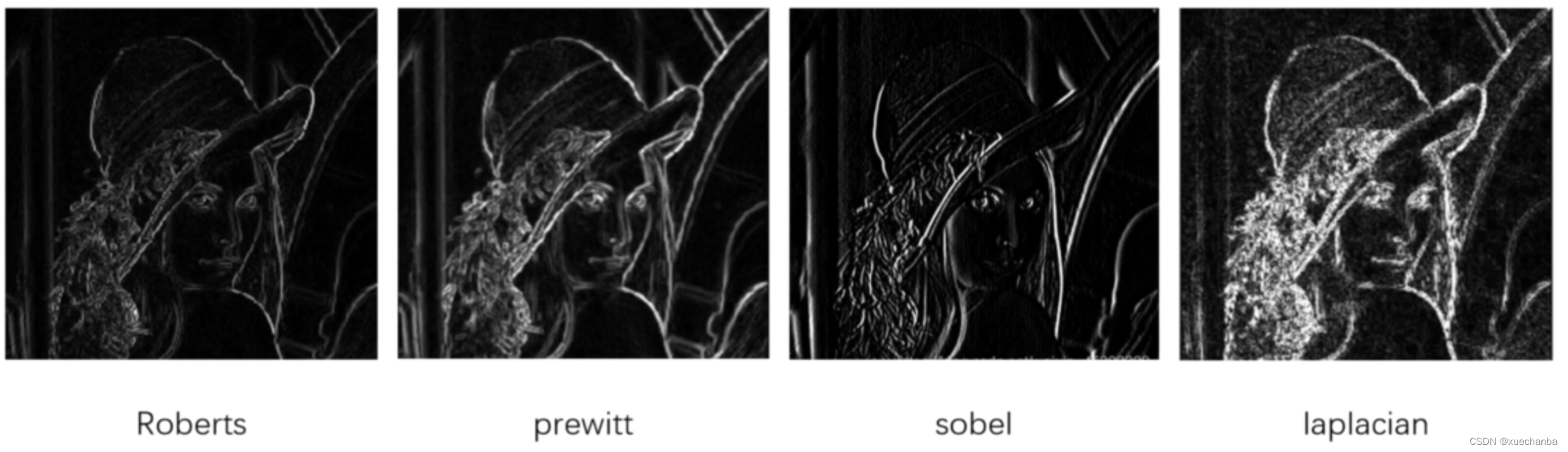
在图像的边缘中,存在着有关图像的大量丰富的信息。
人类在看到物体时,视觉系统首先把图像边缘和背景分离出来,然后才辨认物体中的细节。在计算机视觉系统中,图像分析和理解的第一步常常就是边缘检测。通过边缘检测可以大幅度的减少数据量,在保留重要结构属性的同时,剔除掉不重要的弱相关的信息。
例如,下图所示,在使用淘宝的拍立淘功能时,
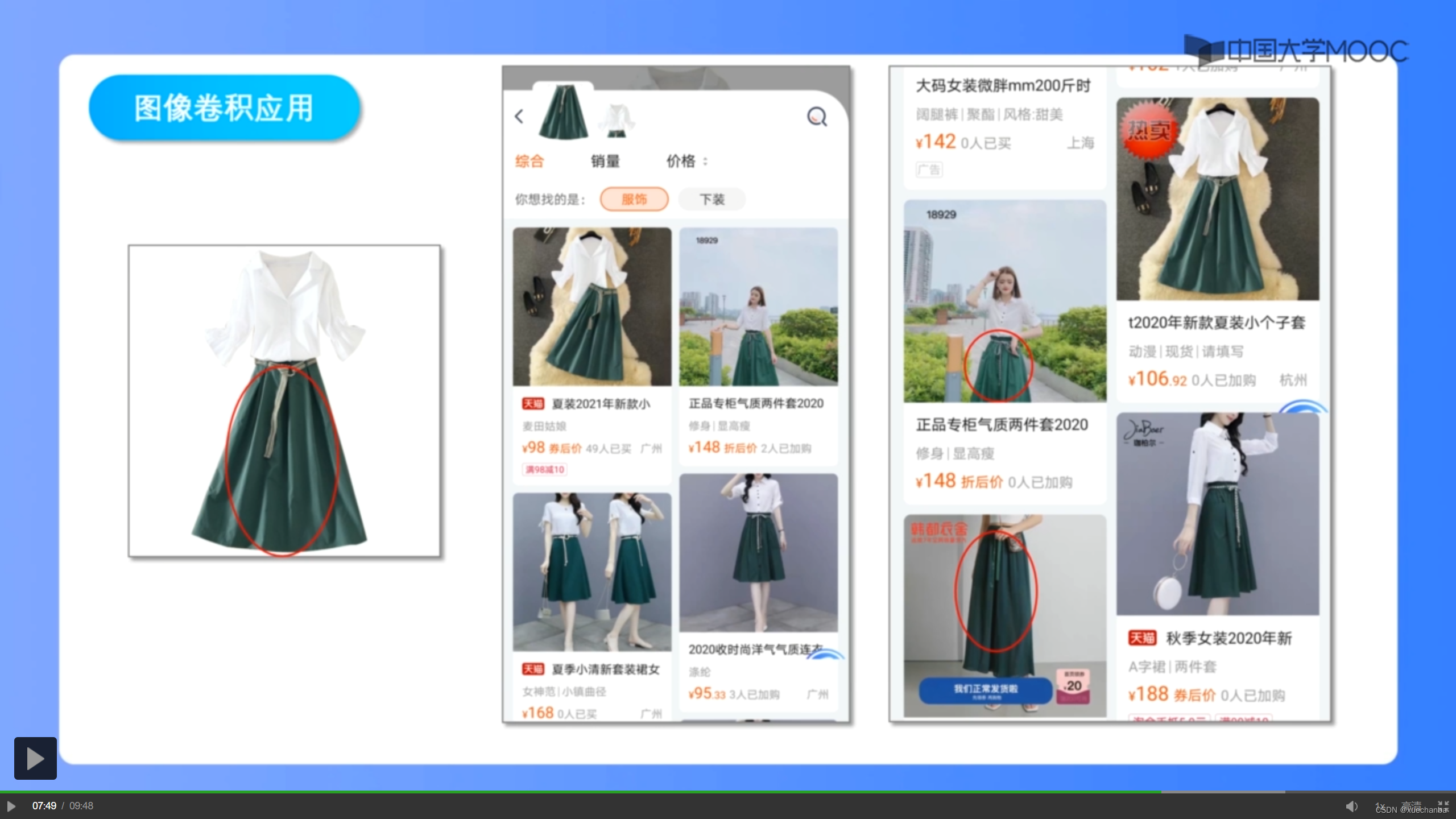
在搜索时,我们主要关心的是款式,而对于腰带、纽扣的细节可能并不是那么敏感。而衣服的款式信息更多的蕴含在衣服的外形、轮廓中。也就是说,我们希望保留衣服的边缘信息。而把颜色、商标之类的细节当作噪声过滤掉,显然,可以通过边缘提取和细节模糊的卷积核完成上述操作。
下图为使用 sobel 算子得到的女装边缘,

通过它可以快速的区分服装的类型。
举例:

在每一组图中,左上角加红色边框的是输入图片,其他是搜索得到的结果。
提取特征
图像的卷积运算可以看做是一种提取图像特征的方式,使用不同的卷积核就可以抽取出不同的图像特征。
例如,我们希望在输入图片中寻找到这样的一个线条特征,
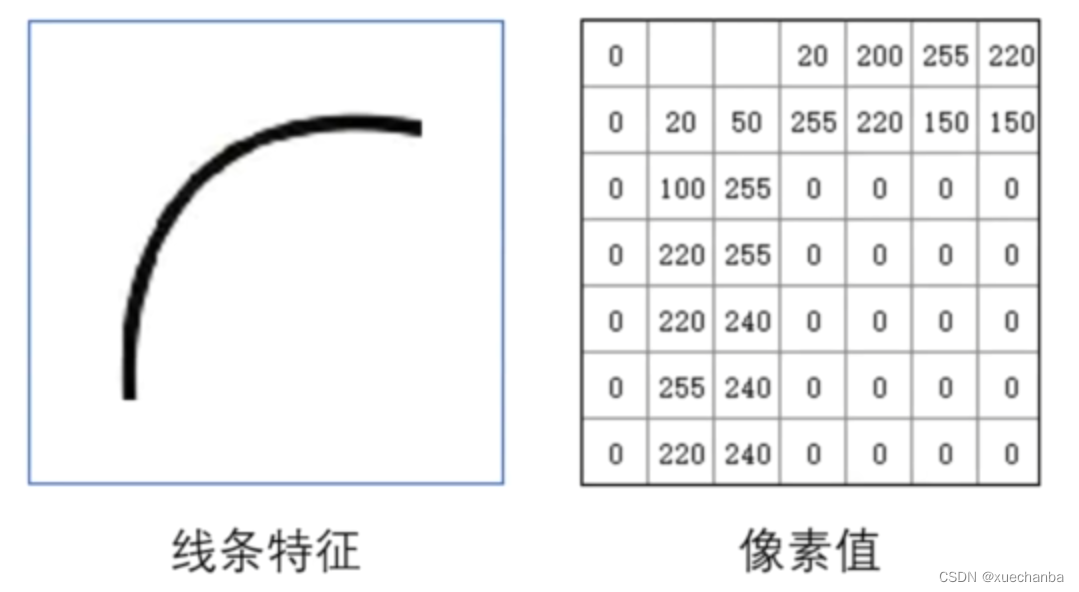
只要为它量身定做一个这样的卷积核就可以了。
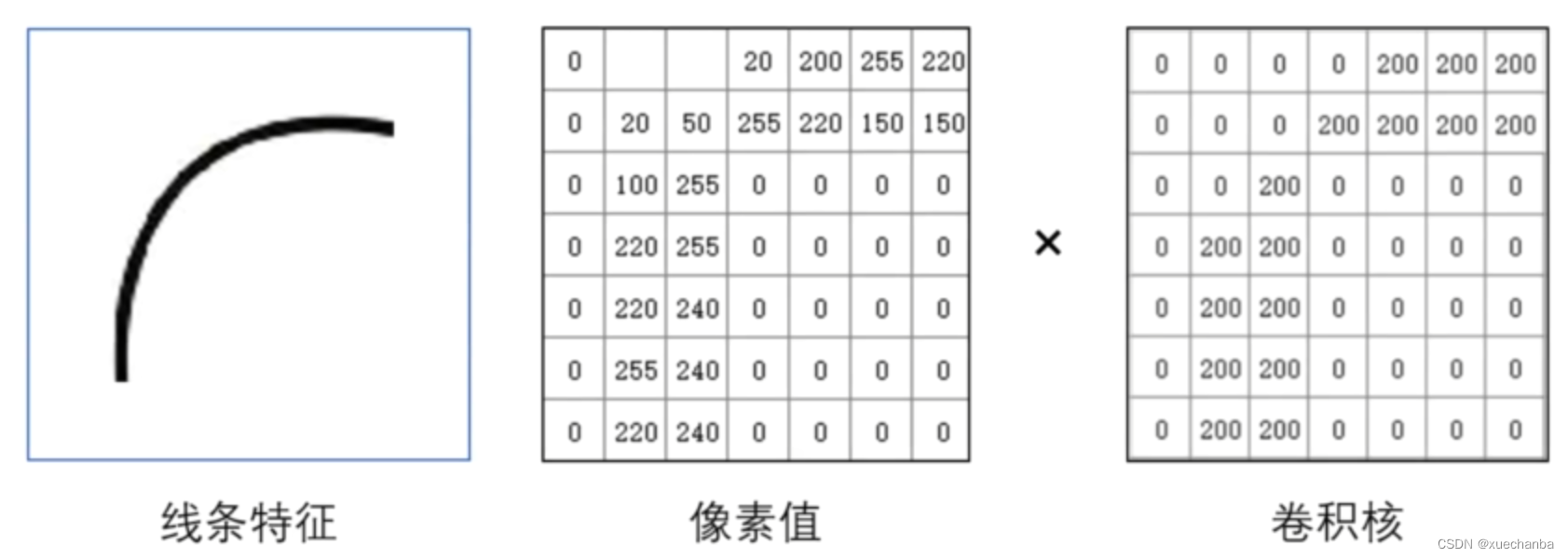
假设这是输入图像,使用卷积核扫描整个图像
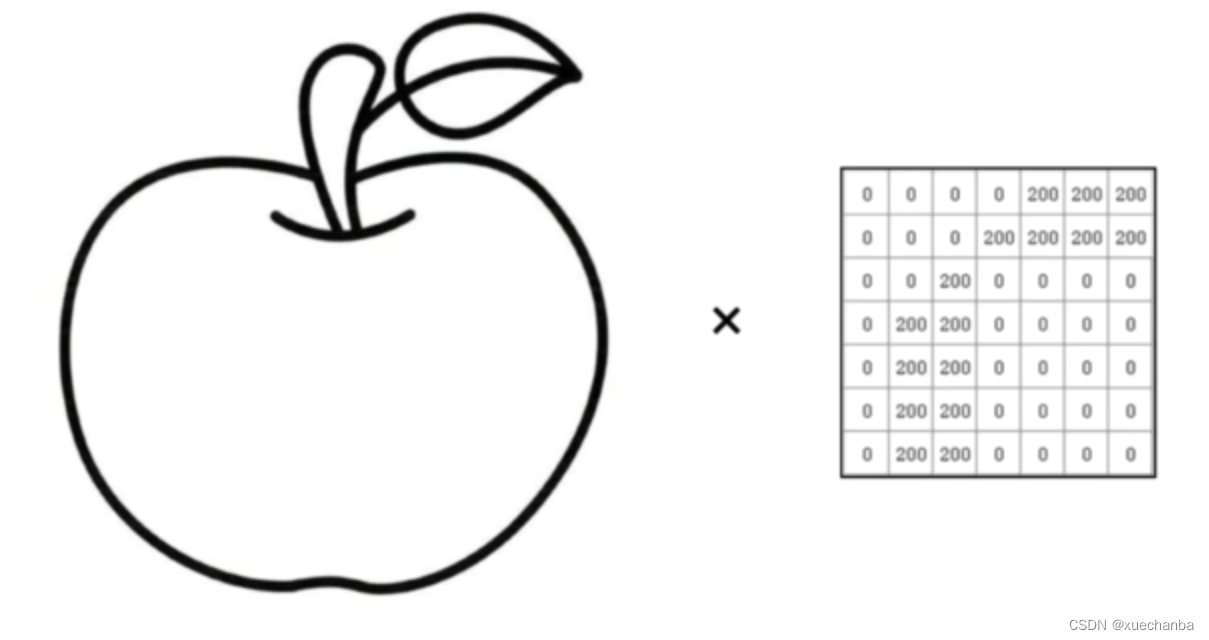
在不匹配的区域内,卷积运算的输出值很小,当卷积窗口到达下图所示区域时,
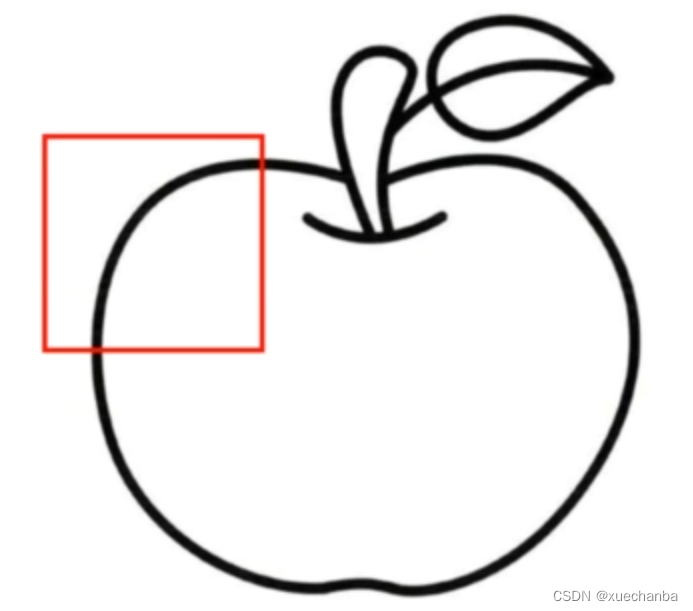
会得到很大输出,就识别出了指定的线条特征。
在下面的这些图中,
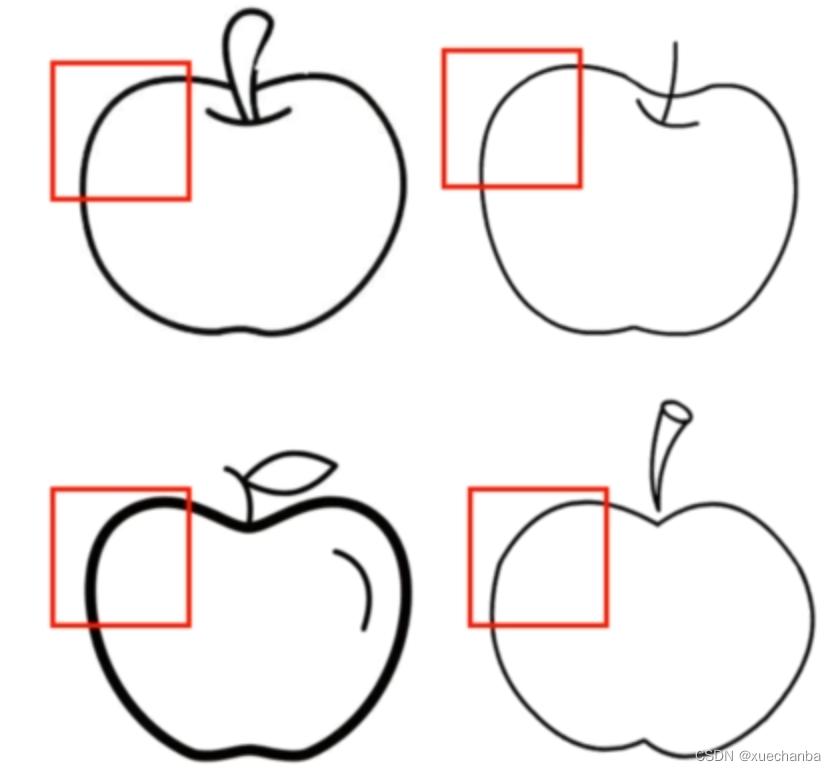
虽然红色框中的线条稍有不同,但是使用这个卷积核仍然可以得到一个比较大的结果,而在图中的其他部分,卷积的计算结果都会非常小。甚至接近于 0 ,因此,仍然能够在一定程度上识别出指定的特征。
如果还需要识别出苹果的其他特征,那么就需要再设计其他的卷积核。
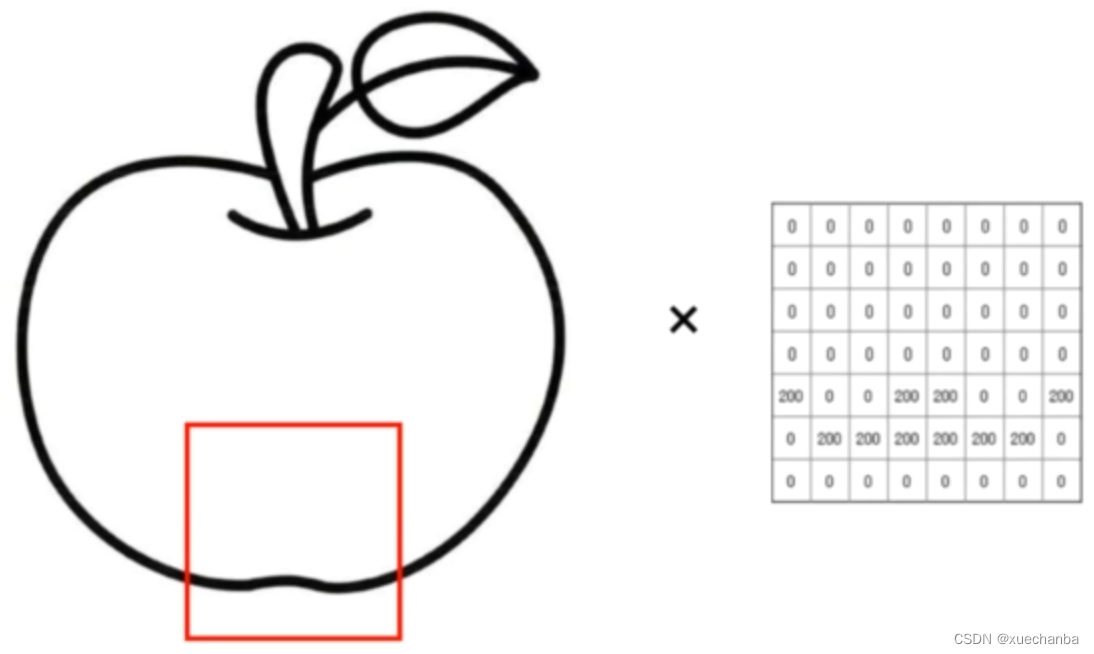
如果一幅图中同时满足了多个苹果的特征,我们就能够识别出简笔画中的苹果了。