目录
1、极大极小游戏
1)题目描述
给你一个下标从 0 开始的整数数组
nums,其长度是2的幂。
对 nums 执行下述算法:
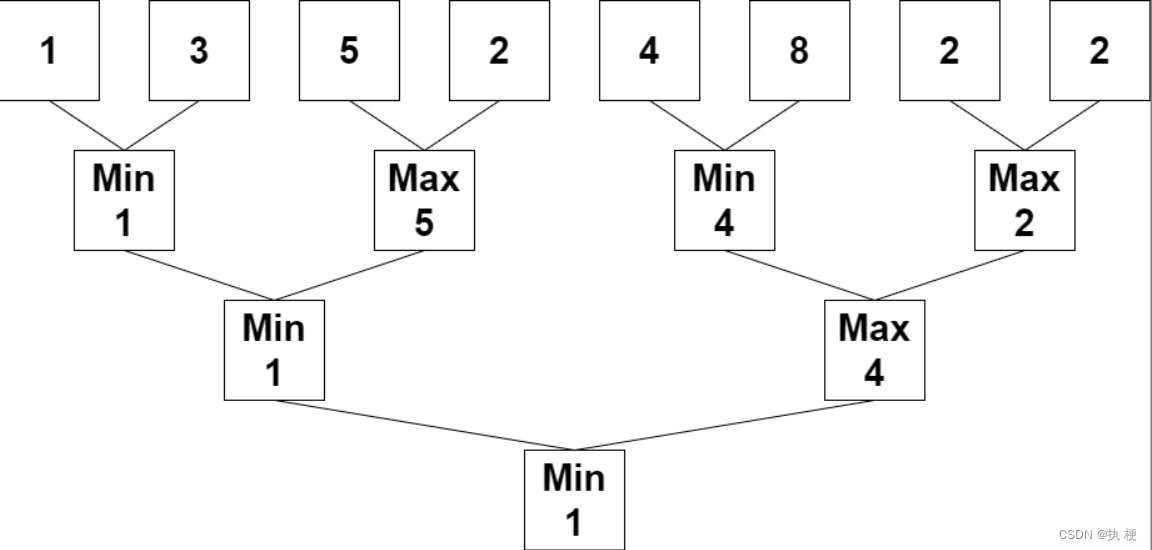
设n等于nums的长度,如果n == 1,终止算法过程。否则,创建 一个新的整数数组newNums,新数组长度为n / 2,下标从 0 开始。
对于满足0 <= i < n / 2的每个 偶数 下标i,将newNums[i]赋值 为min(nums[2 * i], nums[2 * i + 1])。
对于满足0 <= i < n / 2的每个 奇数 下标i,将 newNums[i] 赋值 为max(nums[2 * i], nums[2 * i + 1])。
用newNums替换nums。
从步骤 1 开始 重复 整个过程。
执行算法后,返回 nums 中剩下的那个数字。
2)原题链接
原题链接:LeetCode.6090:极大极小游戏
3)思路解析
- ( 1 ) (1) (1)题意比较清楚,直接模拟即可。
- ( 2 ) (2) (2)使用数组或者队列模拟都行,这里我使用递归,出口则当长度
n为1的时候。
4)模板代码
class Solution {
public int minMaxGame(int[] arr) {
int[] s=test(arr);
return s[0];
}
int[] test(int[] arr){
int n=arr.length;
if (n==1) return arr;
int[] s=new int[n/2];
for (int i = 0; i <n/2; i++) {
if (i%2==0){
s[i]=Math.min(arr[i*2],arr[i*2+1]);
}else{
s[i]=Math.max(arr[i*2],arr[i*2+1]);
}
}
return test(s);
}
}
5)算法与时间复杂度
算法:模拟
时间复杂度:每次递归数组长度减半,总共递归 l o g n logn logn次,时间复杂度为 O ( l o g n ) O(logn) O(logn)。
2、划分数组使最大差为 K
1)题目描述
给你一个整数数组
nums和一个整数k。你可以将nums划分成一个或多个 子序列 ,使 nums 中的每个元素都 恰好 出现在一个子序列中。
在满足每个子序列中最大值和最小值之间的差值最多为k的前提下,返回需要划分的 最少 子序列数目。
子序列 本质是一个序列,可以通过删除另一个序列中的某些元素(或者不删除)但不改变剩下元素的顺序得到。
2)原题链接
3)思路解析
- ( 1 ) (1) (1)由于是子序列而不是子数组,加上需要考虑子序列内的最大值和最小值,我们可以考虑先将数组排序。
- ( 2 ) (2) (2)用指针
pre指向当前最小的数,在它的右边找到最大的满足减去自身的差不超过k的数nxet, [ p r e , n e x t ] [pre,next] [pre,next]这就可以当做一段子序列。 - ( 3 ) (3) (3)更新
pre为next+1,直到整个数组遍历完。由于数组已经排好序,对于第二步我们可以考虑使用二分查找来搜索next。 - ( 4 ) (4) (4)第二步也可以直接遍历数组查找,时间复杂度为 O ( n ) O(n) O(n),没什么太大影响。
4)模板代码
class Solution {
public int partitionArray(int[] arr, int k) {
Arrays.sort(arr);
int n=arr.length;
int pre=0;
int c=0;
while (pre<n){
int l=pre;
int r=n-1;
while (l<r){
int mid=(l+r+1)>>1;
if (arr[mid]-arr[pre]<=k) l=mid;
else r=mid-1;
}
pre=r+1;
c++;
}
return c;
}
}
5)算法与时间复杂度
算法:贪心、排序
时间复杂度:排序的时间复杂度为 O ( n l o g n ) O(nlogn) O(nlogn),每次二分的时间复杂度为 O ( l o g n ) O(logn) O(logn),整体时间复杂度为 O ( n ) O(n) O(n)。
3、替换数组中的元素
1)题目描述
给你一个下标从
0开始的数组nums,它包含 n 个 互不相同 的正整数。请你对这个数组执行m个操作,在第i个操作中,你需要将数字operations[i][0]替换成operations[i][1]。
题目保证在第 i 个操作中:
operations[i][0]在nums中存在。
operations[i][1]在nums中不存在。
请你返回执行完所有操作后的数组。
2)原题链接
3)思路解析
- ( 1 ) (1) (1)每次需要用
x去替换y,所以我们得知道y在原数组中的位置,这一步可以用哈希表存储。arr[i]为key,i为值。 - ( 2 ) (2) (2)一个位置的数有可能被多次替换,所以每次替换完以后我们需要把数再次存入哈希表中。
4)模板代码
class Solution {
Map<Integer,Integer> map=new HashMap<>();
public int[] arrayChange(int[] arr, int[][] s) {
int n=arr.length;
for (int i = 0; i < n; i++) {
map.put(arr[i],i);
}
for (int[] c:s){
int a=c[0];
int b=c[1];
int index=map.get(a);
arr[index]=b;
map.put(b,index);
}
return arr;
}
}
5)算法与时间复杂度
算法:模拟、哈希表
时间复杂度:使用哈希表进行纯模拟操作,时间复杂度为 O ( n ) O(n) O(n)。
4、设计一个文本编辑器
1)题目描述
请你设计一个带光标的文本编辑器,它可以实现以下功能:
添加:在光标所在处添加文本。
删除:在光标所在处删除文本(模拟键盘的删除键)。
移动:将光标往左或者往右移动。
当删除文本时,只有光标左边的字符会被删除。光标会留在文本内,也就是说任意时候0 <= cursor.position <= currentText.length都成立。
请你实现TextEditor类:
TextEditor()用空文本初始化对象。
void addText(string text)将 text 添加到光标所在位置。添加完后光标在 text 的右边。
int deleteText(int k)删除光标左边k个字符。返回实际删除的字符数目。
string cursorLeft(int k)将光标向左移动k次。返回移动后光标左边min(10, len)个字符,其中len是光标左边的字符数目。
string cursorRight(int k)将光标向右移动k次。返回移动后光标左边min(10, len)个字符,其中len是光标左边的字符数目。
2)原题链接
3)思路解析
- ( 1 ) (1) (1)
Java语言使用StringBuilder进行模拟,使用一个变量index模拟光标。indx指向待删除的元素,初始值我们赋值为-1。表示字符串为空。 - ( 2 ) (2) (2)每一步根据题意进行模拟即可,注意对边界的把握。
4)模板代码
class TextEditor {
StringBuilder sb;
int idx;
public TextEditor() {
sb=new StringBuilder();
idx=-1;
}
public void addText(String text) {
sb.insert(idx+1,text);
idx+=text.length();
}
public int deleteText(int k) {
//全部删完
if (idx+1<=k){
sb.delete(0,idx+1);
//System.out.println(sb);
int g=idx;
idx=-1;
return g+1;
}else{
//删除部分
sb.delete(idx+1-k,idx+1);
//System.out.println(sb);
idx-=k;
return k;
}
}
public String cursorLeft(int k) {
idx=Math.max(-1,idx-k);
if (idx==-1) return "";
//长度大于等于10的情况
if (idx>=9) return sb.substring(idx+1-10,idx+1);
return sb.substring(0,idx+1);
}
public String cursorRight(int k) {
idx=Math.min(idx+k,sb.length()-1);
if (idx==-1) return "";
//长度大于等于10的情况
if (idx>=9) return sb.substring(idx+1-10,idx+1);
return sb.substring(0,idx+1);
}
}
5)算法与时间复杂度
算法:模拟
时间复杂度:大模拟题没有分析意义。
5、周赛总结
整体难度较低,但wa了五次,应当反思,多注意细节情况。做之前明确好题意再下手。