文章目录
参考资料
1. PID控制原理
1.1 基本概念
PID( Proportional Integral Derivative)是工业应用最为广泛 的控制器。学习过控制理论的同学对它一定不陌生(毕竟调参这事可以记一辈子呢~~)。
PID控制器(比例-积分-微分控制器),由比例单元(Proportional)、积分单元(Integral)和微分单元(Derivative)组成。可以透过调整这三个单元的增益 K p K_{p} Kp, K i K_{i} Ki和 K d K_{d} Kd来调定其特性。
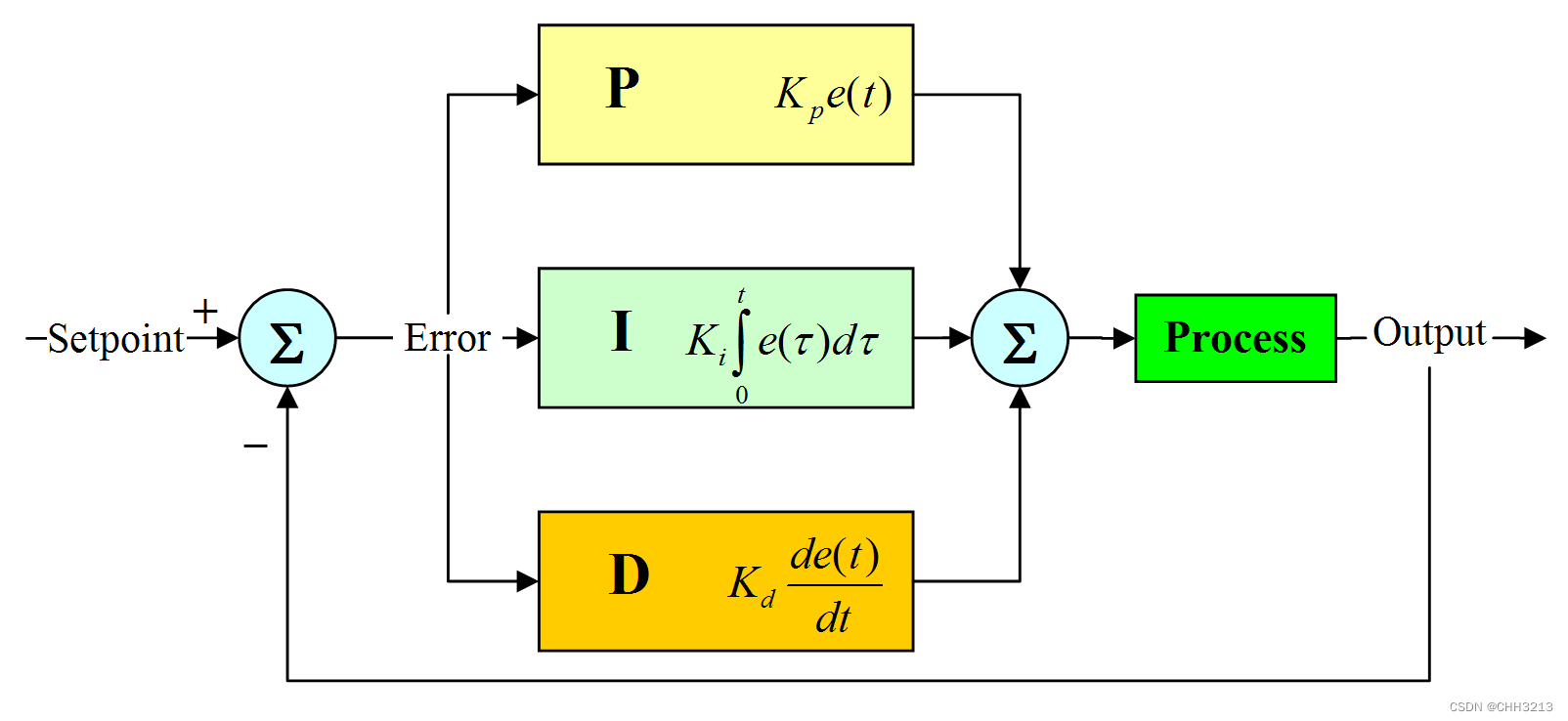
PID算法可以用下式表示:
u ( t ) = K p e ( t ) + K i ∫ 0 t e ( τ ) d τ + K d d d t e ( t ) = K p [ e ( t ) + 1 T i ∫ 0 t e ( τ ) d τ + T d d d t e ( t ) ] (1) \tag{1} \begin{matrix} \mathrm{u}(t)&=K_{p} e(t)+K_{i} \int_{0}^{t} e(\tau) d \tau+K_{d} \frac{d}{d t} e(t)\\ &=K_{p} \left[e(t)+\frac{1}{T_i}\int_{0}^{t} e(\tau) d \tau+T_{d} \frac{d}{d t} e(t)\right] \end{matrix} u(t)=Kpe(t)+Ki∫0te(τ)dτ+Kddtde(t)=Kp[e(t)+Ti1∫0te(τ)dτ+Tddtde(t)](1)
其中
- K p K_{p} Kp : 比例增益,是调适参数
- K i K_{i} Ki : 积分增益,也是调适参数
- K d K_{d} Kd : 微分增益,也是调适参数
- T i T_i Ti:积分时间常数
- T d T_d Td:微分时间常数
- e e e : 误差=设定值 ( S P ) − (\mathrm{SP})- (SP)− 当前值( P V ) \mathrm{PV}) PV)
- t t t : 当前时间
- τ \tau τ : 积分变数,数值从 0 到目前时间 t t t
当被控对象的结构和参数不能完全掌握,或得不到精确的数学模型时,控制理论的其它技术难以采用时,系统控制器的结构和参数必须依靠经验和现场调试来确定,这时应用PID控制技术最为方便。即当我们不完全了解一个系统和被控对象,或不能通过有效的测量手段来获得系统参数时,最适合用PID控制技术。
任何闭环控制系统的首要任务是要稳(稳定)、准(准确)、快(快速)的响应命令。PID的主要工作就是如何实现这一任务。
PID控制器的比例单元§、积分单元(I)和微分单元(D)分别对应目前误差、过去累计误差及未来误差。若是不知道受控系统的特性,一般认为PID控制器是最适用的控制器.
-
增大比例环节将加快系统的响应,它的作用于输出值较快,但不能很好稳定在一个理想的数值,不良的结果是虽较能有效的克服扰动的影响,但有余差出现,过大的比例系数会使系统有比较大的超调,并产生振荡,使稳定性变坏。
-
积分环节能在比例的基础上消除余差,它能对稳定后有累积误差的系统进行误差修整,减小稳态误差。
-
微分环节具有超前作用,对于具有容量滞后的控制通道,引入微分参与控制,在微分项设置得当的情况下,对于提高系统的动态性能指标,有着显著效果,它可以使系统超调量减小,减小震荡,稳定性增加,动态误差减小。
在调整的时候,我们要做的任务就是在系统结构允许的情况下,在这三个参数之间权衡调整,达到最佳控制效果,实现稳、准、快的控制特点。
在实际应用中,主要有以下不足:
1. 在实际工业生产过程往往具有非线性、时变不确定,难以建立精确的数学模型,常规的PID控制器不能达到理想的控制效果;
2. 在实际生产现场中,由于受到参数整定方法烦杂的困扰,常规PID控制器参数往往整定不良、效果欠佳,对运行工况的适应能力很差。
1.2 数字 PID 控制算法
在实际计算机实现时,由于计算机控制是一种采样控制, 它只能根据采样时刻的偏差计算控制量,而不能像模拟控制那样连续输出控制量, 进行连续控制,所以实现的是离散形式的PID,即数字PID控制算法
1. 位置式PID
位置式PID是当前系统的实际位置,与你想要达到的预期位置的偏差,进行PID控制
设采样时间为 T T T ,公式(1)中的积分项可以用下式近似
∫ 0 t e ( τ ) d τ = T ∑ j = 0 k e j \int_{0}^{t} e(\tau) d \tau=T\sum_{j=0}^{k} e_j ∫0te(τ)dτ=Tj=0∑kej
微分项可近似为(后向差分法)
d e ( t ) d t = e k − e k − 1 T \frac{d e\left(t\right)}{d t}=\frac{e_k-e_{k-1}}{T} dtde(t)=Tek−ek−1
故公式(1)化为
u k = K p { e k + T T i ∑ j = 0 k e j + T d T [ e k − e k − 1 ] } = K p e k + K i ∑ j = 0 k e j + K d [ e k − e k − 1 ] (2) \tag{2} \begin{matrix} u_k&=K_{p}\left\{e_k+\frac{T}{T_i} \sum_{j=0}^{k} e_j+\frac{T_{d}}{T}[e_k-e_{k-1}]\right\}\\ &=K_{p} e_k+K_{i} \sum_{j=0}^{k} e_j+K_{d}[e_k-e_{k-1}] \end{matrix} uk=Kp{
ek+TiT∑j=0kej+TTd[ek−ek−1]}=Kpek+Ki∑j=0kej+Kd[ek−ek−1](2)
当采样时间足够小时,能够获得最够精确的结果,离散控制过程与连续过程非常接近。
位置式PID在积分项达到饱和时,误差仍然会在积分作用下继续累积,一旦误差开始反向变化,系统需要一定时间从饱和区退出,所以在 u ( k ) u(k) u(k)达到最大和最小时,要停止积分作用,并且要有积分限幅和输出限幅。
python代码实现
class PID_posi:
"""位置式实现
"""
def __init__(self, k=[1., 0., 0.], target, upper, lower):
self.kp, self.ki, self.kd = k
self.e = 0 # error
self.pre_e = 0 # previous error
self.sum_e = 0 # sum of error
self.target = target # target
self.upper_bound = upper # upper bound of output
self.lower_bound = lower # lower bound of output
def set_target(self, target):
self.target = target
def set_k(self, k):
self.kp, self.ki, self.kd = k
def set_bound(self, upper, lower):
self.upper_bound = upper
self.lower_bound = lower
def cal_output(self, obs): # calculate output
self.e = self.target - obs
u = self.e * self.kp + self.sum_e * \
self.ki + (self.e - self.pre_e) * self.kd
if u < self.lower_bound:
u = self.lower_bound
elif u > self.upper_bound:
u = self.upper_bound
self.pre_e = self.e
self.sum_e += self.e
# print(self.sum_e)
return u
def reset(self):
# self.kp = 0
# self.ki = 0
# self.kd = 0
self.e = 0
self.pre_e = 0
self.sum_e = 0
# self.target = 0
def set_sum_e(self, sum_e):
self.sum_e = sum_e
2. 增量式PID
增量式 PID 是指数字控制器的输出只是控制量的增量 ∆ u k ∆u_k ∆uk 。 当执行机构需要的控制量是增量,而不是位置量的绝对数值时,可以使用增量式 PID 控制算法进行控制。
增量式 PID 控制算法公式为:
Δ u k = u k − u k − 1 = K p ( e k − e k − 1 ) + K i e k + K d ( e k − 2 e k − 1 + e k − 2 ) = K p ( e k − e k − 1 + T T i e k + T d e k − 2 e k − 1 + e k − 2 T ) = K p ( 1 + T T i + T d T ) e k − K p ( 1 + 2 T d T ) e k − 1 + K p T d T e k − 2 ) = A e k + B e k − 1 + C e k − 2 其中 A = K p ( 1 + T T i + T d T ) B = K p ( 1 + 2 T d T ) C = K p T d T (3) \tag{3} \begin{aligned} \Delta u_{k}&=u_{k}-u_{k-1}\\ &=K_p\left(e_k-e_{k-1}\right)+K_ie_k+K_d\left(e_k-2e_{k-1}+e_{k-2}\right)\\ &=K_p\left(e_{k}-e_{k-1}+\frac{T}{T_i} e_{k}+T_d \frac{e_{k}-2 e_{k-1}+e_{k-2}}{T}\right) \\ &=\left.K_p\left(1+\frac{T}{T_i}+\frac{T_d}{T}\right) e_{k}-K_p\left(1+\frac{2 T_d}{T}\right) e_{k-1}+K_p \frac{T_d}{T} e_{k-2}\right) \\ &= A e_{k}+B e_{k-1}+C e_{k-2} \\ \\ \text { 其中 } \quad \mathrm{A} &=K_p\left(1+\frac{T}{T_i}+\frac{T_d}{T}\right) \\ \mathrm{B}&=K_p\left(1+\frac{2 T_d}{T}\right) \\ \mathrm{C}&=K_p \frac{T_d}{T} \end{aligned} Δuk 其中 ABC=uk−uk−1=Kp(ek−ek−1)+Kiek+Kd(ek−2ek−1+ek−2)=Kp(ek−ek−1+TiTek+TdTek−2ek−1+ek−2)=Kp(1+TiT+TTd)ek−Kp(1+T2Td)ek−1+KpTTdek−2)=Aek+Bek−1+Cek−2=Kp(1+TiT+TTd)=Kp(1+T2Td)=KpTTd(3)
增量式PID根据公式可以很好地看出,一旦确定了 K p 、 K i 、 K d K_p、K_i 、K_d Kp、Ki、Kd,只要使用前后三次测量值的偏差, 即可由公式求出控制增量;
得出的控制量 Δ u k \Delta u_k Δuk对应的是近几次位置误差的增量,而不是对应与实际位置的偏差 ,因此没有误差累积。
python代码实现
# 增量式
class PID_inc:
"""增量式实现
"""
def __init__(self, k, target, upper=1., lower=-1.):
self.kp, self.ki, self.kd = k
self.err = 0
self.err_last = 0
self.err_ll = 0
self.target = target
self.upper = upper
self.lower = lower
self.value = 0
self.inc = 0
def cal_output(self, state):
self.err = self.target - state
self.inc = self.kp * (self.err - self.err_last) + self.ki * self.err + self.kd * (
self.err - 2 * self.err_last + self.err_ll)
self._update()
return self.value
def _update(self):
self.err_last = self.err
self.err_ll = self.err_last
self.value = self.value + self.inc
if self.value > self.upper:
self.value = self.upper
elif self.value < self.lower:
self.value = self.lower
def set_target(self, target):
self.target = target
def set_k(self, k):
self.kp, self.ki, self.kd = k
def set_bound(self, upper, lower):
self.upper_bound = upper
self.lower_bound = lower
2. 车辆横向跟踪误差
对于几何路径跟踪一般简化车辆模型为单车模型,如下图所示:

横向跟踪误差(cross track error, 简称CTE)为车辆中心点 ( r x , r y ) (r_x, r_y) (rx,ry)到最近路径点 ( p x , p y ) (p_x, p_y) (px,py)的距离,具体如下图所示。

图中——
- θ e = α − ψ \theta_e=\alpha-\psi θe=α−ψ
- ψ \psi ψ:航向角;
- e y e_y ey:横向跟踪误差
- l d l_d ld:前视距离——后轴中心离当前路点的距离
根据上图,横向跟踪误差(CTE)计算公式如下:
e y = l d sin θ e (4) \tag{4} e_y=l_d\sin{\theta_e} ey=ldsinθe(4)
3. PID实现轨迹跟踪
设车辆运动学模型为以后轴中心为车辆中心的单车运动学模型(具体可参考笔者之前的博客),即
{ x ˙ = V cos ( ψ ) y ˙ = V sin ( ψ ) ψ ˙ = V L tan δ f V ˙ = a \left\{\begin{array}{l} \dot{x}=V \cos (\psi) \\ \dot{y}=V \sin (\psi) \\ \dot{\psi}=\frac{V}{L}\tan{\delta_f}\\ \dot{V}=a \end{array}\right. ⎩⎪⎪⎨⎪⎪⎧x˙=Vcos(ψ)y˙=Vsin(ψ)ψ˙=LVtanδfV˙=a
python实现代码如下。
import math
class KinematicModel_3:
"""假设控制量为转向角delta_f和加速度a
"""
def __init__(self, x, y, psi, v, L, dt):
self.x = x
self.y = y
self.psi = psi
self.v = v
self.L = L
# 实现是离散的模型
self.dt = dt
def update_state(self, a, delta_f):
self.x = self.x+self.v*math.cos(self.psi)*self.dt
self.y = self.y+self.v*math.sin(self.psi)*self.dt
self.psi = self.psi+self.v/self.L*math.tan(delta_f)*self.dt
self.v = self.v+a*self.dt
def get_state(self):
return self.x, self.y, self.psi, self.v
位置式和增量式PID的实现代码前文已给出。
下一步,还需要计算参考轨迹上离车辆当前位置最近的航路点:
def cal_target_index(robot_state,refer_path):
"""得到临近的路点
Args:
robot_state (_type_): 当前车辆位置
refer_path (_type_): 参考轨迹(数组)
Returns:
_type_: 最近的路点的索引
"""
dists = []
for xy in refer_path:
dis = np.linalg.norm(robot_state-xy)
dists.append(dis)
min_index = np.argmin(dists)
return min_index
这部分可以使用KDTree来搜索搜索最临近的航路点,KDTree的使用可以参考资料
主函数入口(部分参考自资料1):
from scipy.spatial import KDTree
from celluloid import Camera # 保存动图时用,pip install celluloid
# set reference trajectory
refer_path = np.zeros((1000, 2))
refer_path[:,0] = np.linspace(0, 100, 1000) # 直线
refer_path[:,1] = 2*np.sin(refer_path[:,0]/3.0)#+2.5*np.cos(refer_path[:,0]/2.0) # 生成正弦轨迹
refer_tree = KDTree(refer_path) # reference trajectory
# 假设初始状态为x=0,y=-1,偏航角=0.5rad,前后轴距离2m,速度为2m/s,时间步为0.1秒
ugv = KinematicModel_3(0,-1,0.5,2,2,0.1)
k=0.1
c=2
x_ = []
y_ = []
fig = plt.figure(1)
# 保存动图用
camera = Camera(fig)
for i in range(550):
robot_state = np.zeros(2)
robot_state[0] = ugv.x
robot_state[1] = ugv.y
distance, ind = refer_tree.query(robot_state) # 在参考轨迹上查询离robot_state最近的点
# ind = cal_target_index(robot_state,refer_path) # 使用简单的一个函数实现查询离robot_state最近的点,耗时比较长
alpha = math.atan2(refer_path[ind, 1]-robot_state[1], refer_path[ind, 0]-robot_state[0])
l_d = np.linalg.norm(refer_path[ind]-robot_state)
# l_d = k*ugv.v+c # 前视距离
theta_e = alpha-ugv.psi
e_y = -l_d*math.sin(theta_e) # 与博客中公式相比多了个负号,我目前还不是太理解,暂时先放着
# e_y = -l_d*np.sign(math.sin(theta_e)) # 第二种误差表示
# e_y = robot_state[1]-refer_path[ind, 1] #第三种误差表示
# PID.set_target(0)
# print(refer_path[i,1])
delta_f = PID.cal_output(e_y)
# print(e_y)
# print(alpha)
ugv.update_state(0,delta_f) # 加速度设为0
x_.append(ugv.x)
y_.append(ugv.y)
# 显示动图
plt.cla()
plt.plot(refer_path[:, 0], refer_path[:, 1], '-.b', linewidth=1.0)
plt.plot(x_, y_, "-r", label="trajectory")
plt.plot(refer_path[ind, 0], refer_path[ind, 1], "go", label="target")
# plt.axis("equal")
plt.grid(True)
plt.pause(0.001)
# camera.snap()
# animation = camera.animate()
# animation.save('trajectory.gif')
plt.figure(2)
plt.plot(refer_path[:, 0], refer_path[:, 1], '-.b', linewidth=1.0)
plt.plot(x_,y_,'r')
plt.show()
使用PID得到的跟踪效果大致如下图所示

完整的Python代码可以参考github仓库。