【自动驾驶】学习卡尔曼滤波（二）——扩展卡尔曼滤波

参考资料

• 如何使用卡尔曼滤波（Kalman Filtering）实现对物体运动轨迹的预测？
• 卡尔曼滤波与目标追踪
• 卡尔曼滤波算法原理

文章大部分内容是根据参考资料整理所得，旨在于更方便学习记忆查找，不作其他用途。

在上一篇整理总结了基本的卡尔曼滤波后，这一章来学习扩展卡尔曼滤波（EKF)，由于许多符号在上一篇中已经说明，所以本篇讲解中不再赘述。

1. 基本概念

如下式，当状态转移矩阵（过程模型）和观测矩阵（观测模型）为非线性时，基础的卡尔曼滤波就无法发挥用处了，由此引入了扩展卡尔曼滤波。

$$x_k=g(u_k,x_{k-1})+{\omega }_k$$

$$z_k=h(x_k)+v_k$$

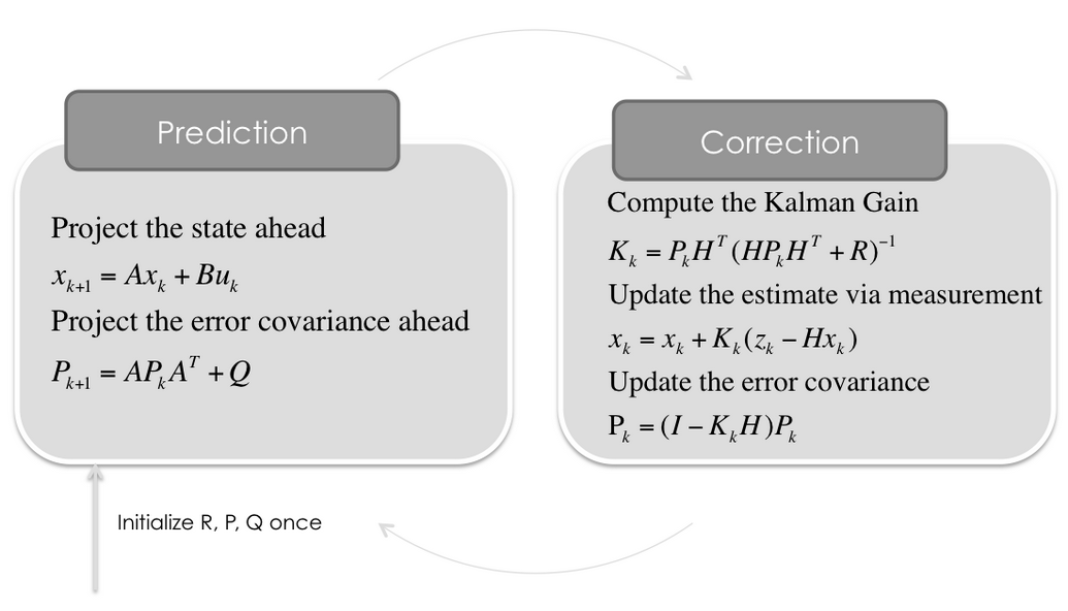
对以上非线性函数进行泰勒展开，可化为线性形式。所以，扩展卡尔曼滤波算法只比原始卡尔曼滤波算法多了一步线性化的工作。具体流程如下图：

可以发现，他与线性的卡尔曼滤波差别不大：

1.1 线性化过程——雅可比矩阵

在向量微积分中，雅可比矩阵是一阶偏导数以一定方式排列成的矩阵，其行列式称为雅可比行列式。

雅可比矩阵的重要性在于它体现了一个可微方程与给出点的最优线性逼近。因此，雅可比矩阵类似于多元函数的导数。

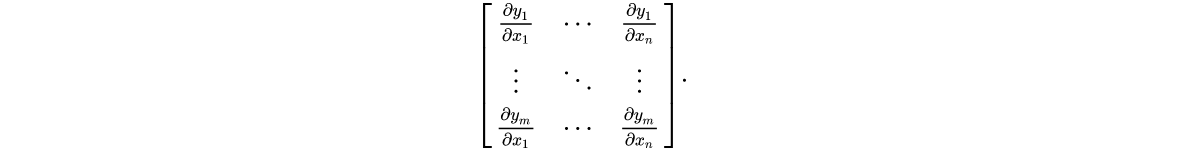
1.2 预测

故原本状态方程和观测方程中的$A,H$矩阵（或者用$F,H$符号表示，本文主要使用$F,H$表示，如果图片中出现了$A,H$，意思是一样的），在非线性系统中用雅可比矩阵代替

所以预测阶段的公式变为：

1.3 更新

更新方程相对于KF而言，主要变动如下：

$$\begin{array}{rl}& {\hat{y}}_k=z_k-h\left({\hat{x}}_{k\mid k-1},0\right)\\ & S_k=J_H{P}_{k\mid k-1}{J}_H^T+R_k\\ & K_k=P_{k\mid k-1}{J}_H^T{S}_k^{-1}\\ & {\hat{x}}_{k\mid k}={\hat{x}}_{k\mid k-1}+K_k{\hat{y}}_k\\ & P_{k\mid k}=\left(I-K_k{J}_H\right)P_{k\mid k-1}\end{array}$$

2. 移动机器人应用

本节内容主要来自博客。

2.1 移动机器人运动学模型（过程模型）

• 连续运动学模型:
  $$\left\{\begin{array}{c}\dot{x}=v\cos (\varphi )\\ \dot{y}=v\sin (\varphi )\\ \dot{\varphi }=\omega \end{array}\right\}\text{\hspace{1em}(1)}$$

• 离散化后模型:
  $$\left\{\begin{array}{c}{x}_t=x_{t-1}+d_{t}v\cos (\varphi )\\ y_t=y_{t-1}+d_{t}v\sin (\varphi )\\ {\varphi }_t={\varphi }_{t-1}+d_t{\omega }_t\end{array}\right\}\text{\hspace{1em}(2)}$$

  设移动机器人在时间 $t$ 时刻的状态为四维向量 ${\mathbf{x}}_t$ ​：

  $${\mathbf{x}}_t=[x_t,y_t,{\varphi }_t,v_t{]}^T$$

  • $x_t$为二维笛卡尔坐标系的X轴坐标值；
  • $y_t$​为二维笛卡尔坐标系的Y轴坐标值；
  • ${\varphi }_t$为移动机器人的航向角；
  • $v_t$为移动机器人的行驶线速度。

  设状态转移噪声方差为 $R$，观测噪声方差为 $Q$。

  移动机器人装载有速度传感器与陀螺仪，可分别测量时刻$t$的速度与角速度为:
  $${\mathbf{u}}_t=[v_t,{\omega }_t{]}^T$$

• 状态向量为 ${\mathbf{x}}_t={\left[x_t,y_t,{\varphi }_t,v_t\right]}^T$ ，输入控制量为 ${\mathbf{u}}_t={\left[v_t,{\omega }_t\right]}^T$ ，可得状态转移函数为:
  $${\mathbf{x}}_t=F{\mathbf{x}}_{t-1}+B{\mathbf{u}}_t$$
  $$F=\left[\begin{array}{cccc}1.0& 0& 0& 0\\ 0& 1.0& 0& 0\\ 0& 0& 1.0& 0\\ 0& 0& 0& 0\end{array}\right]$$
  $$B=\left[\begin{array}{cc}{d}_t\cos \left({\varphi }_t\right)& 0\\ d_t\sin \left({\varphi }_t\right)& 0\\ 0& d_t\\ 1.0& 0\end{array}\right]$$

2.2 雅可比矩阵

由于控制向量的系数矩阵 $B$ 中包含状态量 ${\varphi }_t$ ，所以上面的状态转移函数为非线性。利用式 (2),我们可以得到状态函数的Jacobian矩 阵 $J_F$ :
$$J_F=\left[\begin{array}{llll}\frac{dx}{dx}& \frac{dx}{dy}& \frac{dx}{d\varphi }& \frac{dx}{dv}\\ \frac{dy}{dx}& \frac{dy}{dy}& \frac{dy}{d\varphi }& \frac{dy}{dv}\\ \frac{d\varphi }{dx}& \frac{d\varphi }{dy}& \frac{d\varphi }{d\varphi }& \frac{d\varphi }{dv}\\ \frac{dv}{dx}& \frac{dv}{dy}& \frac{dv}{d\varphi }& \frac{dv}{dv}\end{array}\right]=\left[\begin{array}{cccc}1& 0& -v\sin (\varphi )dt& \cos (\varphi )dt\\ 0& 1& v\cos (\varphi )dt& \sin (\varphi )dt\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$$

2.3 观测模型

假定移动机器人装载有GNSS（卫星导航定位）传感器，可以实时获得自身的位置作为自身的观测向量${\mathbf{z}}_t$ ​

$${\mathbf{z}}_t=[x_t,y_t{]}^T$$

使用矩阵表示即
$$\begin{array}{c}{\mathbf{z}}_t=H{\mathbf{x}}_t\\ H=\left[\begin{array}{cccc}1.0& 0& 0& 0\\ 0& 1.0& 0& 0\end{array}\right]\end{array}$$

2.4 PYTHON代码实现

该部分见于github仓库。