程序员的内功心法-红黑树

从上篇《2-3-4树的插入和删除》了解到了底层原理和操作的逻辑思路。尽管我们完成了平衡树的逻辑，但按照对应逻辑实现代码和各种情况的处理，却不容易。所以我们要减少由于2-3-4树为了实现平衡，而导致的实现复杂度上升的情况。我们现在使用普通的二叉树+颜色来表示2-3-4树（红黑树是多路平路查找树的一种实现）

红黑树的定义：

文章里的红黑树的定义了参考《算法》第四版

红链接必须是左链接，根结点必须是黑色的
不能同时存在两条连续的红链接
任一空链接到根节点的路径上经历的黑色节点个数一样

下面我们使用1-3的插入来观察红黑树是如何保持平衡的？

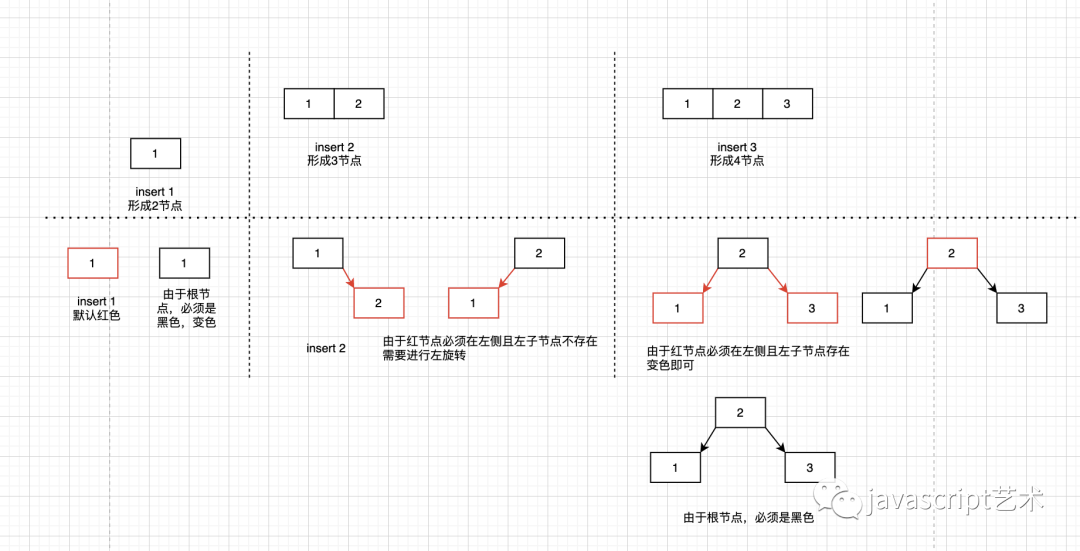
根据上面根据上面的操作我们可以发现红黑树对2-3-4树的实现原理：

使用黑+红两个节点来实现3节点（如上图插入2后）
使用三个黑色节点实现4节点（如上图插入3后）

节点对象的定义

RedBlackNode<T extends Comparable<T>> {

    /*颜色的常量定义 red:false black:true 新建节点默认为红色*/
    public static final boolean RED = false;

    public static final boolean BLACK = true;

    private T data;
    
    private RedBlackNode<T> left;

    private RedBlackNode<T> right;

    private boolean color;
}

操作

我们将红黑树的操作分开描述

查找

查找和普通的二叉搜索树一致，不再赘叙。

可以参考二叉搜索树关于查找的部分

旋转和变色

左旋转

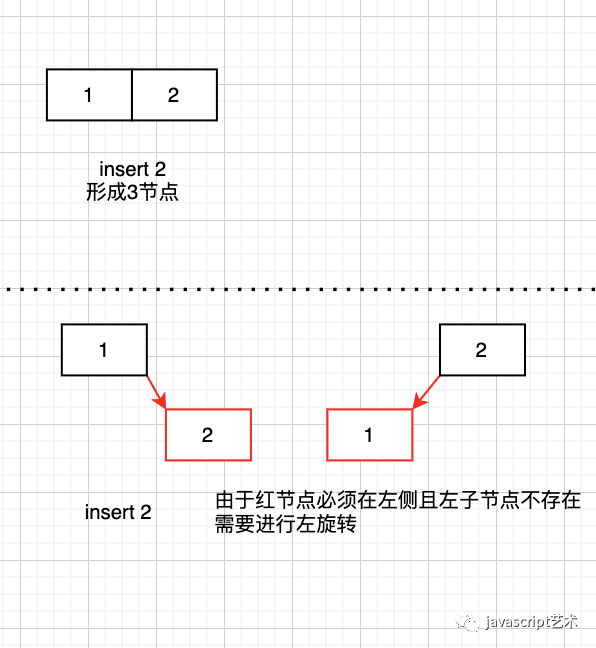
实现步骤：

右子节点的颜色 = 原根结点的颜色
根结点node作为右子节点的左子节点，刷新为红色节点
将右子节点的左子节点设置为原根结点的右子节点

代码示例：

RedBlackNode<T> rotateLeft(RedBlackNode<T> node){
    RedBlackNode<T> right = node.getRight();
    right.setColor(node.isColor());

    RedBlackNode<T> middle = right.getLeft();
    node.setRight(middle);
    node.setColor(RedBlackNode.RED);
    right.setLeft(node);
    return right;
}

右旋转

将根结点的左子节点替换到根结点，将左子节点作为根结点返回

实现步骤：

左子节点的颜色 = 原根结点的颜色
根结点node替换到左子节点的右子节点，刷新为红色节点
将左子节点的右子节点设置为原根结点的左子节点

代码示例：

RedBlackNode<T> rotateRight(RedBlackNode<T> node){
    RedBlackNode<T> result = node.getLeft();
    result.setColor(node.isColor());

    RedBlackNode<T> resultRight = result.getRight();
    node.setLeft(resultRight);

    result.setRight(node);
    node.setColor(RedBlackNode.RED);
    return result;
}

变色

/**如果左右节点都是红色的那么将左右子节点修改为黑色，父节点修改为红色*/
void flushColor(RedBlackNode<T> node){
    node.setColor(RedBlackNode.RED);
    RedBlackNode<T> left = node.getLeft();
    left.setColor(RedBlackNode.BLACK);
    RedBlackNode<T> right = node.getRight();
    right.setColor(RedBlackNode.BLACK);
}

插入

向2节点插入

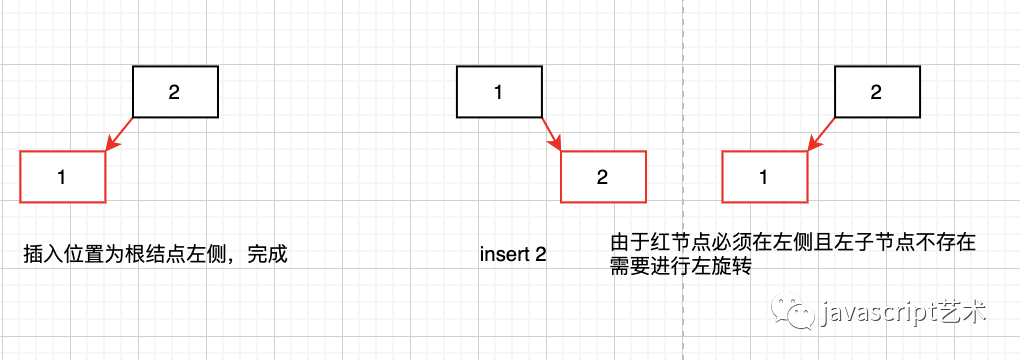
向3节点插入

插入算法代码示例：

RedBlackNode<T> insert(RedBlackNode<T> node, T data){
    if (Objects.isNull(node)) {
        node = new RedBlackNode<>();
        node.setData(data);
        node.setColor(RedBlackNode.RED);
        return node;
    }
    T nodeData = node.getData();
    int flag = data.compareTo(nodeData);
    if (flag < 0) { //插入数据小于节点数据，入左子树
        RedBlackNode<T> left = insert(node.getLeft(), data);
        node.setLeft(left);
    } else if (flag > 0) {  //插入数据大于节点数据，入右子树
        RedBlackNode<T> right = insert(node.getRight(), data);
        node.setRight(right);
    }
    //插入位置在右子节点，且左子树非红色，进行左旋转
    if (isRed(node.getRight()) && !isRed(node.getLeft())) {
        node = rotateLeft(node);
    }
    //插入的节点在左子树的左子节点上，右旋
    if (isRed(node.getLeft()) && isRed(node.getLeft().getLeft())) {
        node = rotateRight(node);
    }
    if (isRed(node.getLeft()) && isRed(node.getRight())) {
        flushColor(node);
    }
    return node;
}

删除

由于我们在二叉搜索树BST里介绍过，我们可以将节点删除的逻辑调整为极值的删除

2-3-4树文章里，已经知道单独的2节点是不能直接删除的，需要将2节点转换为3或4节点（2节点对应红黑树中的黑色节点）

综上所述：我们需要极大/小值的删除和2节点的删除方法

删除最小值

主要分为3节点和4节点删除最小值(其中4节点根结点有红或黑两种颜色。CASE比较多，请放大查看)

代码示例：

/**
最小值的删除方法，返回删除后的根节点
*/
RedBlackNode<T> deleteMin(RedBlackNode<T> node){
    RedBlackNode<T> left = node.getLeft();
    //左节点不为null，最小值在node的左节点,继续向左
    if (Objects.isNull(left)) {
        return null;
    }
    //左右节点都不是红色,需要将黑色节点调整为红色Del-2至Del-5示
    RedBlackNode<T> ll = left.getLeft();
    if (!isRed(left) && !isRed(ll)) {
        node = removeRedLeft(node);
    }
    left = deleteMin(node.getLeft());
    node.setLeft(left);
    return blance(node);
}
/** 移除红色最小节点
*/
RedBlackNode<T> removeRedLeft(RedBlackNode<T> node) {
    flipsColor(node);
    RedBlackNode<T> right = node.getRight();
    RedBlackNode<T> rl = Objects.isNull(right) ? null : right.getLeft();
    //如果右左节点是红色节点(对应图中的Del-3、Del-5图)
    if (isRed(rl)) {
        right = rotateRight(right);
        node.setRight(right);
        node = rotateLeft(node);
    }
    return node;
}

/**变色Del-2至Del-5示*/
void flipsColor(RedBlackNode<T> node) {
    node.setColor(RedBlackNode.BLACK);
    RedBlackNode<T> left = node.getLeft();
    RedBlackNode<T> right = node.getRight();
    if (Objects.nonNull(left)) {
        left.setColor(RedBlackNode.RED);
    }
    if (Objects.nonNull(right)) {
        right.setColor(RedBlackNode.RED);
    }
}

/**
节点删除后的平衡调整方法
*/
RedBlackNode<T> balance(RedBlackNode<T> node){
    if (isRed(node.getRight())) {       //右节点为红，左旋（图中的2列）
        node = rotateLeft(node);
    }
    if (isRed(node.getRight()) && !isRed(node.getLeft())) {
        node = rotateLeft(node);
    }
    if (isRed(node.getLeft()) && isRed(node.getLeft().getLeft())) {
        node = rotateRight(node);
    }
    if (isRed(node.getLeft()) && isRed(node.getRight())) {
        flushColor(node);
    }
    return node;
}

删除最大值

最大值的删除逻辑如下图示

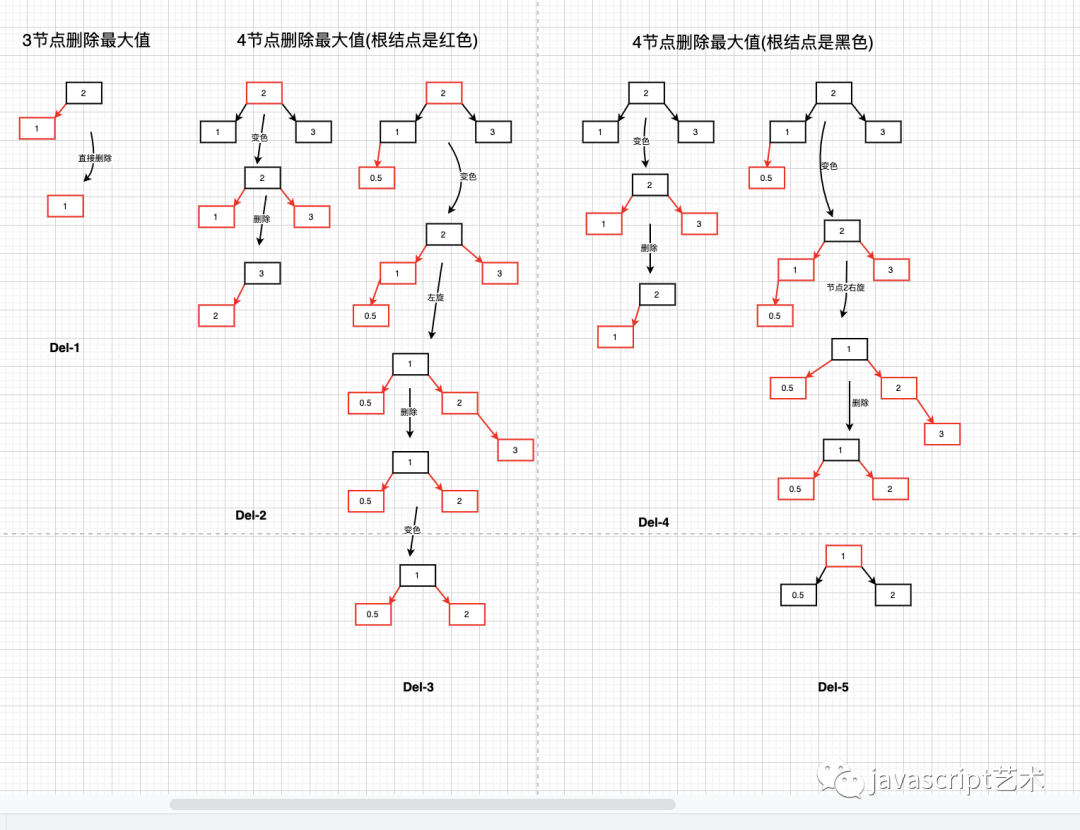
代码示例：

/**
最大值的删除方法，返回删除后的根节点
*/
RedBlackNode<T> deleteMax(RedBlackNode<T> node){
    if(isRed(node.getLeft())){
        node = rotateRight;
    }
    RedBlackNode<T> right = node.getRight();
    if(right == null){
        return null;
    }
    if (!isRed(right) && !isRed(right.getLeft())) {
        node = removeRedRight(node);
    }
    right = deleteMax(right);
    node.setRight(right);
    return balance(node);
}
/** 移除红色右节点
*/
RedBlackNode<T> removeRedRight(RedBlackNode<T> node) {
    flipsColor(node);
    RedBlackNode<T> left = node.getLeft();
    RedBlackNode<T> lr = Objects.isNull(left) ? null : left.getRight();
    //如果左右节点是红色节点
    if (!isRed(rl)) {
        return rotateRight(node);
    }
    return node;
}