目录导航
线性表
线性表是最简单、最基本、最常用的数据结构。其结构中的数据元素之间是一对一的线性关系。即:(1)除第一个位置的数据元素外,其他数据元素的前面都只有一个元素 ;(2)除最后一个位置的数据元素外,其他数据元素位置的后面都只有一个元素。
线性表的接口定义
/// 线性表的接口
public interface IListDS<T>
{
/// <summary>
/// 求长度
/// 初始条件:线性表存在;
/// 操作结果:返回线性表中所有数据元素的个数。
/// </summary>
/// <returns></returns>
int GetLength();
/// <summary>
/// 清空操作
/// 初始条件:线性表存在且有数据元素;
/// 操作结果:从线性表中清除所有数据元素,线性表为空
/// </summary>
void Clear();
/// <summary>
/// 判断线性表是否为空
/// 初始条件:线性表存在
/// 操作结果:如果线性表为空返回true,否则返回false
/// </summary>
bool IsEmpty();
/// <summary>
/// 附加操作
/// 初始条件:线性表存在且未满
/// 操作结果:将值为item的新元素添加到表的末尾
/// </summary>
void Append(T item);
/// <summary>
/// 插入操作
/// 初始条件:线性表存在,插入位置正确(1<=i<=n+1,n为插入前的表长)
/// 操作结果:在线性表的第i个位置上插入一个值为item的新元素,这样使得原序号为i,i+1,...,n的数据元素序号变为i+1,i+2,...,n+1,插入后表长为原表长+1。
/// </summary>
void Insert(T item, int i);
/// <summary>
/// 删除操作
/// 初始条件:线性表存在且不为空,删除位置正确(1<=i<=n,n为删除前的表长)
/// 操作结果:在线性表中删除序号为i的数据元素,返回删除后的数据元素。删除后使原序号为i+1,i+2,...,n的数据元素的序号变为i,i+1,...,n-1,删除后表原表长-1。
/// </summary>元素
T Delete(int i);
/// <summary>
/// 取表元
/// 初始条件:线性表存在,所取数据元素位置正确(1<=i<=n,n为线性表的表长)
/// 操作结果:返回线性表中第i个数据元素。
/// </summary>
T GetElem(int i);
/// <summary>
/// 按值查找
/// 初始条件:线性表存在
/// 操作结果:在线性表职工查找值为value的数据元素,其结果返回在线性表中首次出现值为value的数据元素的序号,成为查找成功;否则在线性表中未找到值为value的数据元素,返回一个特殊值表示查找失败。
/// </summary>
int Locate(T value);
/// <summary>
/// 元素倒置
/// 线性表存在
/// 操作结果,将线性表中的元素前后倒置。
/// </summary>
void Reverse();
}
这里定义接口为IlistDS是为了和.net框架中的接口Ilist区分,在Ilist后面加了DS,DS表示数据结构。
顺序表
顺序表的存储方式是指在内存中用一块地址连续的空间依次存放线性表的数据元素,特点是在表中相邻的数据元素在内存中存储位置也相邻。存储结构示意图如下:

假设顺序表中的每个数据元素占w个存储单元,设第i个数据元素的存储地址为Loc(ai),则有:
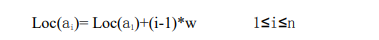
式中的Loc(ai)表示第一个数据元素a1的存储地址,称为顺序表的基地址。
顺序表的实现
public class SeqList<T> : IListDS<T>//继承顺序表的接口
{
private int maxSize;//顺序表的容量
private T[] data;//数组,用于存储顺序表中的数据元素
private int last;//指示顺序表最后一个元素的位置
//索引器,用于获取元素
public T this[int index]
{
get {
return data[index]; }
set {
data[index] = value; }
}
//最后一个数据元素位置属性
public int Last
{
get {
return last; }
}
//容量属性
public int MaxSize
{
get {
return maxSize; }
set {
maxSize = value; }
}
//构造器
public SeqList(int size)
{
data = new T[size];
maxSize = size;
last = -1;
}
}
实现顺序表接口的方法:
获得元素的操作
取表元运算是返回顺序表中第i个数据元素,i的取值范围是1<=i<=last+1。其算法实现如下:
public T GetElem(int i)
{
if (IsEmpty()||(i<1)||(i>last+1))//判断是否为空或取出位置是否正确
{
Console.WriteLine("list is empty or position is error");
return default(T);//返回该类型(T)的默认值
}
return data[i - 1];
}
插入操作
插入算法的思路:
- 如果插入位置不正确,抛出异常;
- 如果线性表长度大于等于数组长度,则抛出异常或动态增加容量;
- 从最后一个元素开始向前遍历到第i个位置,分别将它们都向后移动一个位置;
- 将要插入元素填入位置i处;
- 表长加1。
插入算法实现如下:
public void Insert(T item, int i)
{
if (IsFull())
{
Console.WriteLine("list is full");
return;
}
//判断插入的位置是否正确
// i小于1表示在第1个位置之前插入
// i大于last+2表示在最后一个元素后面的第2个位置插入
if (i<1||i>last+2)
{
Console.WriteLine("position is error");
return;
}
//在顺序表的表尾插入数据元素
if (i==last+2)
{
data[last + 1] = item;
}
else //在表的其它位置插入数据元素
{
//元素移动,从最后一个位置向前遍历到第i个位置
for (int j = last; j>= i-1; --j)
{
data[j + 1] = data[j];
}
data[i - 1] = item;//将新的数据元素插入到第i个位置上
}
++last;//表长+1
}
删除操作
删除算法的思路:
- 如果删除位置不正确,抛出异常;
- 取出删除元素;
- 从删除元素位置开始遍历到最后一个元素的位置,分别将它们都向前移动一个位置
- 表长减1。
删除算法的实现:
public T Delete(int i)
{
T tmp = default(T);
if (IsEmpty())
{
Console.WriteLine("list is empty");
return tmp;
}
//判断删除的位置是否正确
// i小于1表示删除第1个位置之前的元素
// i大于last+1表示删除最后一个元素后面的第1个位置的元素
if (i<1||i>last+1)
{
Console.WriteLine("position is error");
return tmp;
}
//删除最后一个元素
if (i==last+1)
{
tmp = data[last--];
}
else //删除其他元素
{
tmp = data[i - 1];
for (int j = i; j <= last; ++j)
{
data[j-1] = data[j];//将删除位置后继元素前移
}
}
--last;
return tmp;
}
求顺序表的长度
因为数组的最小索引从0开始,所以,顺序表的长度就是数组总最后一个元素的索引 last+1。
即:
public int GetLength()
{
return last + 1;
}
清空操作
清除顺序表中的元素是使顺序表为空,即 last等于-1。
即:
public void Clear()
{
last = -1;
}
判断顺序表是否为空
如果顺序表的last为-1,则顺序表为空,返回true,否则返回false。
即:
public bool IsEmpty()
{
if (last==-1)
{
return true;
}
else
{
return false;
}
}
判断顺序表是否为满
如果顺序表为满,last等于maxSize-1,返回true,否则返回false。
即:
public bool IsFull()
{
if (last==maxSize-1)
{
return true;
}
else
{
return false;
}
}
附加操作
是指在顺序表未满的情况下,在表的末端添加一个新元素,然后使顺序表的last加1。
附加算法的实现如下:
public void Append(T item)
{
if (IsFull())
{
Console.WriteLine("list is full");
return;
}
data[++last] = item;
}
按值查找
在顺序表中查找值为value的数据元素,如果存在该值,查找成功,则返回顺序表首次出现该值的索引;否则查找失败,返回-1。
public int Locate(T value)
{
if (IsEmpty())
{
Console.WriteLine("list is empty");
return -1;
}
int i = 0;
for (i = 0; i <=last ; i++)
{
//顺序表中存在与给定值相等的元素
if (value.Equals(data[i]))
{
break;
}
}
//表中不存在与给定值相等的元素
if (i>last)
{
return -1;
}
return i;
}
顺序表的应用—元素倒置
因为线性表都可以进行倒置操作,所以可以再IlistDS接口中声明该倒置方法,然后在线性表类中实现即可。
实现思路:
遍历顺序表中元素,把第一个元素与最后一个元素交换,把第二个元素与倒数第二个元素交换,依次类推。规律是,把第i个元素与第n-i个元素交换,i的取值范围是0到n/2,闭开区间,即( [0,n/2) )。
算法实现如下:
public void Reverse()
{
if (IsEmpty())
{
Console.WriteLine("list is empty");
return;
}
T tmp = default(T);
int len = GetLength();
//遍历顺序表,首尾进行元素交换
for (int i = 0; i < len/2; i++)
{
tmp = data[i];
data[i] = data[len - i];
data[len - i] = tmp;
}
}
顺序存储结构的优缺点
优点
- 无须为表示表中元素之间的逻辑关系而增加额外的存储空间
- 可以快速地存取表中任一位置的元素
缺点
- 插入和删除操作需要移动大量元素
- 当线性表长度变化较大时,难以确定存储空间的容量
- 造成存储空间的“碎片”