基于双边滤波(BF)的红外弱小目标检测之背景抑制
1. 前言
红外图像中的弱小目标,目标属性包涵“弱"和“小’’两个方面:“弱’’是指目标在红外波长上所表现出来的强度,具体反映到所拍摄的红外图像上,就是指目标的灰度值;而“小’’是指目标的尺寸大小,也就是前面所述的成像面积很小,反映到红外图像上就是指目标所占的像素数目很少。
SPIE国际光学工程学会(Societyof Photo一0ptical Instrumentation Engineers,简记为SPIE)从1989年开始,几乎每年都会举办有关弱小目标检测技术的国际会议,研讨弱小目标检测技术的最新研究成果。根据SPIE的定义,成像尺寸小于整个成像区域0.12%的目标均可称为弱小目标(即当成像尺寸为256×256时,弱小目标应不超过81个像素,其目标尺寸在9*9以内)。
2. 双边滤波算法
双边滤波的思想是抑制与中心像素差别太大的像素。高斯滤波是以距离为权重,设计滤波模板作为滤波系数,只考虑了像素间的空间位置上的关系,因此滤波的结果会丢失边缘的信息。高斯滤波的缺陷:平坦区域正常滤波,图像细节没有变化,而在突变的边缘上,因为只使用了距离来确定滤波权重,导致边缘被模糊。
在高斯基础上,进一步优化,叠加了像素值的考虑,因此也就引出了双边滤波,一种非线性滤波,滤波效果对保留边缘更有效。为了理解双边滤波的距离和像素差两个影响因素,先说明下面两个概念帮助理解。
(1)空间距离:当前点距离滤波模板中心点的欧式距离。
(2)灰度距离:当前点距离滤波模板中心点的灰度的差值的绝对值。
因此,双边滤波的核函数是空间域核与像素范围域核的综合结果:
(1)在图像的平坦区域,像素值变化很小,那么像素差值接近于0,对应的像素范围域权重接近于1,此时空间域权重起主要作用,相当于进行高斯模糊;
(2)在图像的边缘区域,像素值变化很大,那么像素差值大,对应的像素范围域权重变大,即使距离远空间域权重小,加上像素域权重总的系数也较大,从而保护了边缘的信息。
双边滤波在突变的边缘上,使用了像素差权重,所以很好的保留了边缘。
3. Matlab仿真
%% 测试算法2(双边滤波):对双边滤波算法进行红外弱小目标检测跟踪的性能进行检验
%% 1,根据双边滤波进行背景抑制,在通用数据集上进行验证背景抑制
%% 图像分辨率为 256 × 256,仿真图像位数为 8 bit,目标最小1个像素
% date:2019-11-20 08:43:40
% author:C.S
clc;clear;close;
tic
% function infradDepartion
f=imread('190.bmp');
if ndims(f)>2
f=rgb2gray(f);
end;
[l1,l2]=size(f);
f = double(f);
sigmaSpatial = min(l1,l2)/20;
samplingSpatial=sigmaSpatial;
sigmaRange = (max(f(:))-min(f(:)))/(20*255);
samplingRange= sigmaRange;
f1 = bilateralFilter(f./255,f./255,sigmaSpatial, sigmaRange, ...
samplingSpatial, samplingRange);
f2 = double(zeros(l1,l2));
for i=1:l1
for j=1:l2
if f1(i,j)<f(i,j)
f2(i,j)=f(i,j)-f1(i,j);
% else
% f1(i,j)=1;
end;
end;
end;
means=mean2(f2);
stds=std2(f2);
v=means+stds*3;
for i=1:l1
for j=1:l2
if f2(i,j)<v
f2(i,j)=0;
% else
% f1(i,j)=1;
end;
end;
end;
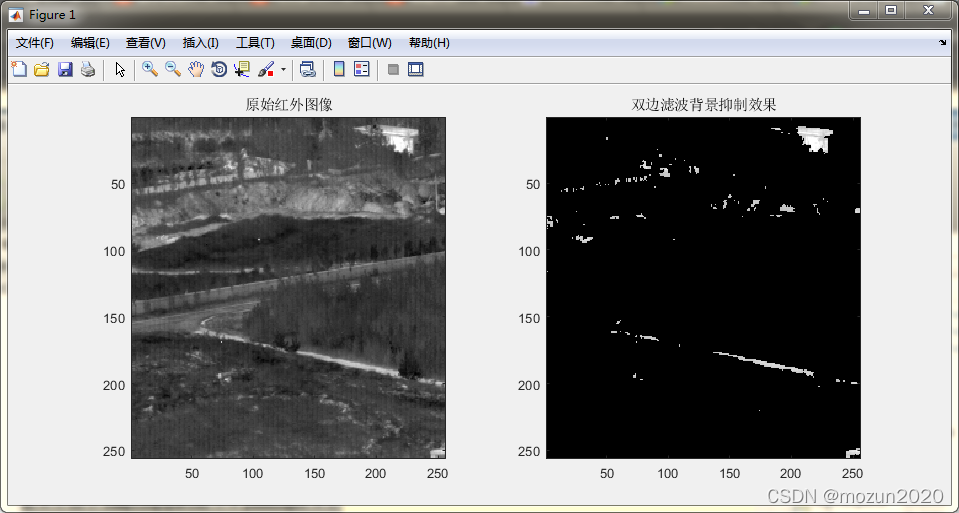
figure(1);subplot(121);
imagesc(f);
title('原始红外图像');
colormap('gray');
subplot(122);
imagesc(uint8(f2));
title('双边滤波背景抑制效果');
colormap('gray');
% end
function output = bilateralFilter( data, edge, sigmaSpatial, sigmaRange, ...
samplingSpatial, samplingRange )
if ~exist( 'edge', 'var' ),
edge = data;
end
inputHeight = size( data, 1 );
inputWidth = size( data, 2 );
if ~exist( 'sigmaSpatial', 'var' ),
sigmaSpatial = min( inputWidth, inputHeight ) / 16;
end
edgeMin = min( edge( : ) );
edgeMax = max( edge( : ) );
edgeDelta = edgeMax - edgeMin;
if ~exist( 'sigmaRange', 'var' ),
sigmaRange = 0.1 * edgeDelta;
end
if ~exist( 'samplingSpatial', 'var' ),
samplingSpatial = sigmaSpatial;
end
if ~exist( 'samplingRange', 'var' ),
samplingRange = sigmaRange;
end
if size( data ) ~= size( edge ),
error( 'data and edge must be of the same size' );
end
% parameters
derivedSigmaSpatial = sigmaSpatial / samplingSpatial;
derivedSigmaRange = sigmaRange / samplingRange;
paddingXY = floor( 2 * derivedSigmaSpatial ) + 1;
paddingZ = floor( 2 * derivedSigmaRange ) + 1;
% allocate 3D grid
downsampledWidth = floor( ( inputWidth - 1 ) / samplingSpatial ) + 1 + 2 * paddingXY;
downsampledHeight = floor( ( inputHeight - 1 ) / samplingSpatial ) + 1 + 2 * paddingXY;
downsampledDepth = floor( edgeDelta / samplingRange ) + 1 + 2 * paddingZ;
gridData = zeros( downsampledHeight, downsampledWidth, downsampledDepth );
gridWeights = zeros( downsampledHeight, downsampledWidth, downsampledDepth );
% compute downsampled indices
[ jj, ii ] = meshgrid( 0 : inputWidth - 1, 0 : inputHeight - 1 );
di = round( ii / samplingSpatial ) + paddingXY + 1;
dj = round( jj / samplingSpatial ) + paddingXY + 1;
dz = round( ( edge - edgeMin ) / samplingRange ) + paddingZ + 1;
% perform scatter (there's probably a faster way than this)
% normally would do downsampledWeights( di, dj, dk ) = 1, but we have to
% perform a summation to do box downsampling
for k = 1 : numel( dz ),
dataZ = data( k ); % traverses the image column wise, same as di( k )
if ~isnan( dataZ ),
dik = di( k );
djk = dj( k );
dzk = dz( k );
gridData( dik, djk, dzk ) = gridData( dik, djk, dzk ) + dataZ;
gridWeights( dik, djk, dzk ) = gridWeights( dik, djk, dzk ) + 1;
end
end
% make gaussian kernel
kernelWidth = 2 * derivedSigmaSpatial + 1;
kernelHeight = kernelWidth;
kernelDepth = 2 * derivedSigmaRange + 1;
halfKernelWidth = floor( kernelWidth / 2 );
halfKernelHeight = floor( kernelHeight / 2 );
halfKernelDepth = floor( kernelDepth / 2 );
[gridX, gridY, gridZ] = meshgrid( 0 : kernelWidth - 1, 0 : kernelHeight - 1, 0 : kernelDepth - 1 );
gridX = gridX - halfKernelWidth;
gridY = gridY - halfKernelHeight;
gridZ = gridZ - halfKernelDepth;
gridRSquared = ( gridX .* gridX + gridY .* gridY ) / ( derivedSigmaSpatial * derivedSigmaSpatial ) + ( gridZ .* gridZ ) / ( derivedSigmaRange * derivedSigmaRange );
kernel = exp( -0.5 * gridRSquared );
% convolve
blurredGridData = convn( gridData, kernel, 'same' );
blurredGridWeights = convn( gridWeights, kernel, 'same' );
% divide
blurredGridWeights( blurredGridWeights == 0 ) = -2; % avoid divide by 0, won't read there anyway
normalizedBlurredGrid = blurredGridData ./ blurredGridWeights;
normalizedBlurredGrid( blurredGridWeights < -1 ) = 0; % put 0s where it's undefined
blurredGridWeights( blurredGridWeights < -1 ) = 0; % put zeros back
% upsample
[ jj, ii ] = meshgrid( 0 : inputWidth - 1, 0 : inputHeight - 1 ); % meshgrid does x, then y, so output arguments need to be reversed
% no rounding
di = ( ii / samplingSpatial ) + paddingXY + 1;
dj = ( jj / samplingSpatial ) + paddingXY + 1;
dz = ( edge - edgeMin ) / samplingRange + paddingZ + 1;
% interpn takes rows, then cols, etc
% i.e. size(v,1), then size(v,2), ...
output = interpn( normalizedBlurredGrid, di, dj, dz );
end
4. 小结
双边滤波是一种非线性滤波器,它可以达到保持边缘、降噪平滑的效果。在视网膜、血管检测中应用较多,本次应用在复杂背景下弱小目标的背景抑制中,后续试经过优化,选出综合效果最好的进行详细介绍。
本系列文章列表如下:
弱小目标检测跟踪算法研究(1)红外弱小目标数据集准备(红外弱小目标的数据集来了)
弱小目标检测跟踪算法研究(2)红外弱小目标数据集准备(红外弱小目标的数据集又来了)
弱小目标检测跟踪算法研究(3) 基于局部对比度(LCM)的红外弱小目标检测之背景抑制
弱小目标检测跟踪算法研究(4) 基于双边滤波(BF)的红外弱小目标检测之背景抑制
弱小目标检测跟踪算法研究(5) 基于顶帽变换(Top_hat)算法的红外弱小目标检测之背景抑制
弱小目标检测跟踪算法研究(6) 基于小波变换的红外弱小目标检测之背景抑制
弱小目标检测跟踪算法研究(7) 基于简单平滑滤波算法的红外弱小目标检测之背景抑制