数据结构（初阶）—— 二叉树② ---链式结构

目录

一、二叉树的遍历问题

二、 二叉树链式结构实现

1.二叉树的结构设计

2.创建二叉树及初始化 

3.二叉树的前序遍历

4.二叉树的中序遍历 

5.二叉树的后续遍历 

6.二叉树的结点个数 

7.二叉树叶子结点个数 

8.二叉树第k层的结点给个数

9.二叉树的深度/高度 

10.二叉树查找值为x的节点 

11.二叉树层序遍历 

12.判断是否为完全二叉树 

13.二叉树的销毁 

三、源代码 

Queue.h 

Queue.c 

test.c

运行效果 

---

一、二叉树的遍历问题

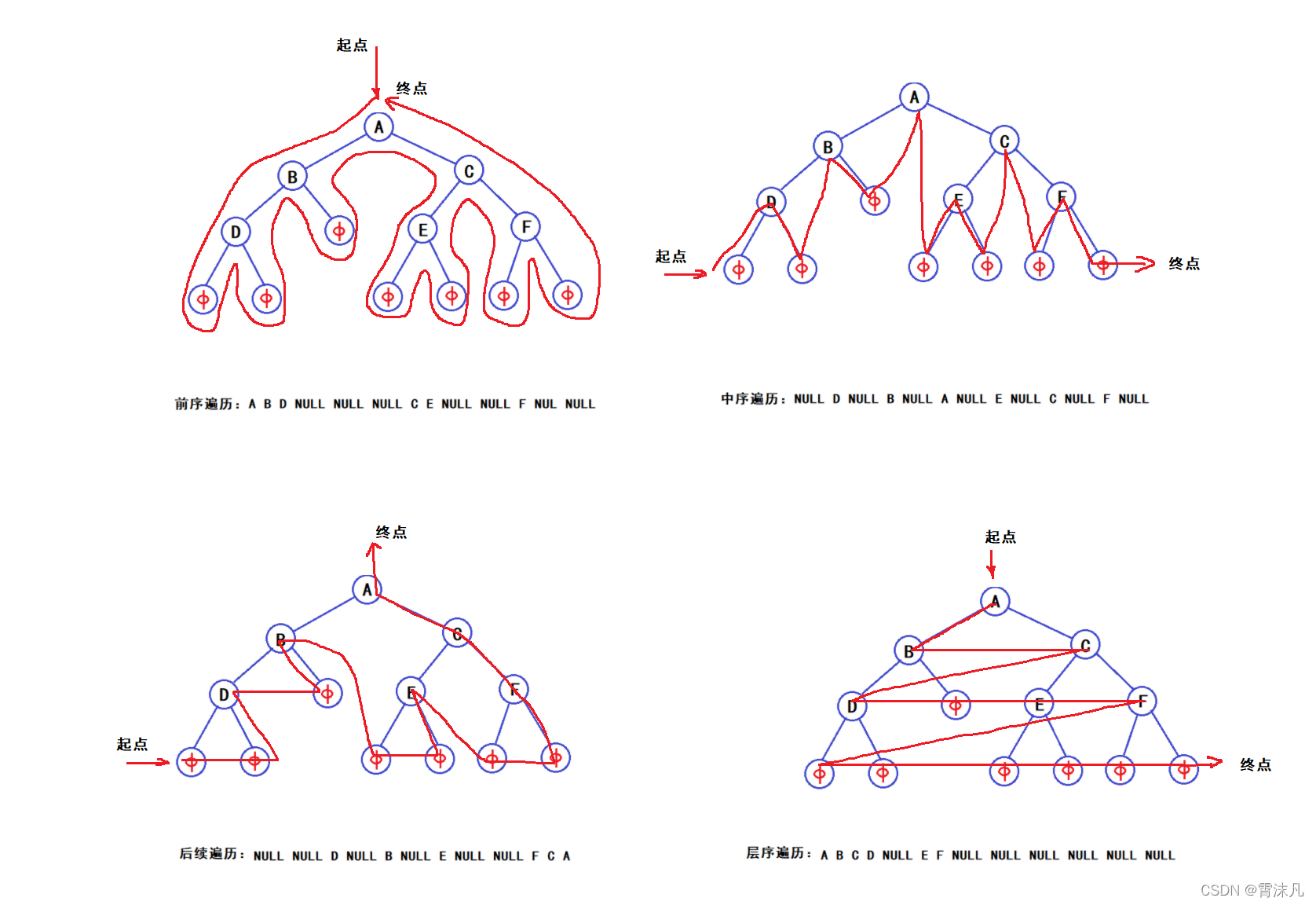
二叉树的遍历分为：前序遍历、中序遍历、后续遍历和层序遍历；

方法：（前提：树不为空）

        前序遍历：访问根结点—>遍历左子树—>遍历右子树；（根、左、右）

        中序遍历：遍历左子树—>访问根结点—>遍历右子树；（左、根、右）

        后续遍历：遍历左子树—>遍历右子树—>访问根结点；（左、右、根）

        层序遍历：从上至下，从左至右顺序访问；

示例：

二、 二叉树链式结构实现

1.二叉树的结构设计

typedef char BTDataType;
typedef struct BinaryTreeNode
{
	BTDataType data;//结点
	struct BinaryTreeNode* left;//左子树
	struct BinaryTreeNode* right;//右子树
}BTNode;

2.创建二叉树及初始化 

  

//二叉树的初始化
BTNode* BuyNode(BTDataType x)
{
	BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
	if (newnode == NULL)
	{
		printf("malloc fail\n");
		exit(-1);
	}
	newnode->data = x;
	newnode->left = newnode->right = NULL;
	return newnode;
}

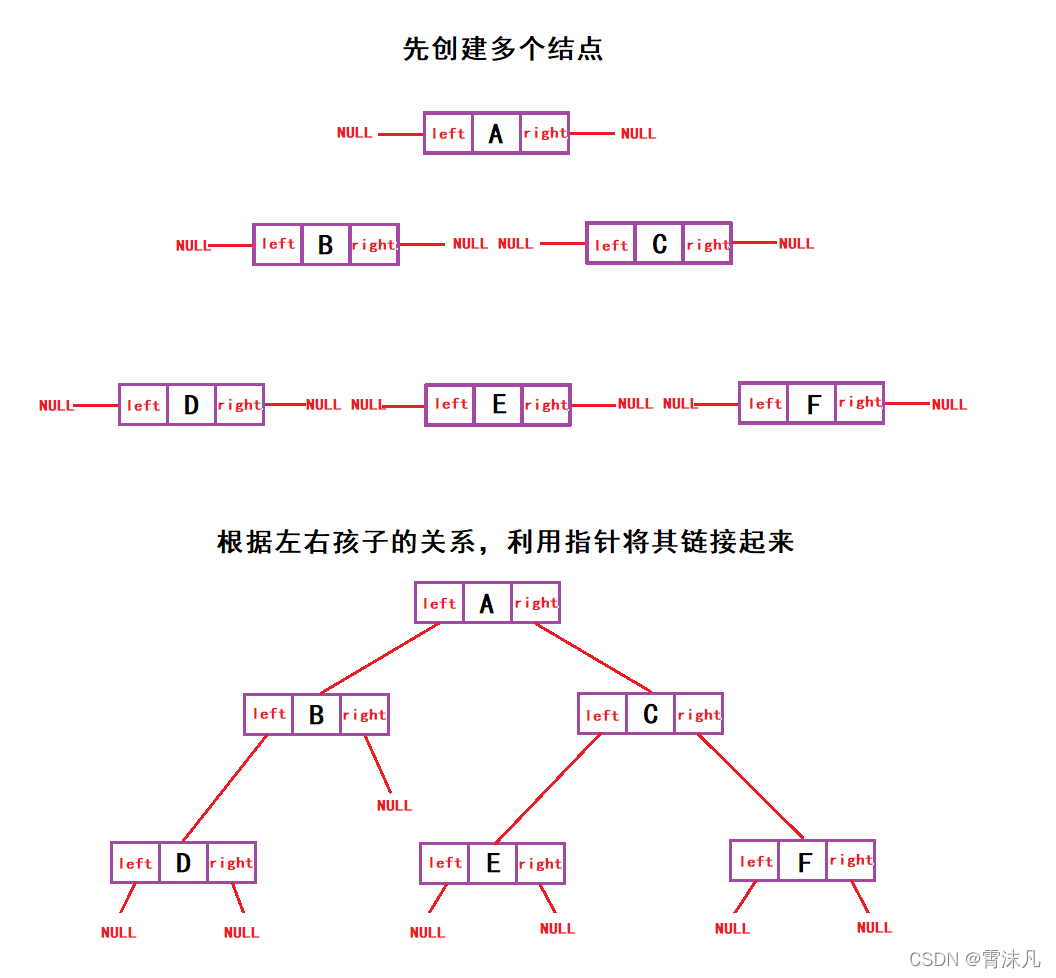
//创建二叉树
BTNode* CreatBinaryTree()
{
	BTNode* nodeA = BuyNode('A');
	BTNode* nodeB = BuyNode('B');
	BTNode* nodeC = BuyNode('C');
	BTNode* nodeD = BuyNode('D');
	BTNode* nodeE = BuyNode('E');
	BTNode* nodeF = BuyNode('F');

	nodeA->left = nodeB;
	nodeA->right = nodeC;
	nodeB->left = nodeD;
	nodeC->left = nodeE;
	nodeC->right = nodeF;
	return nodeA;
}

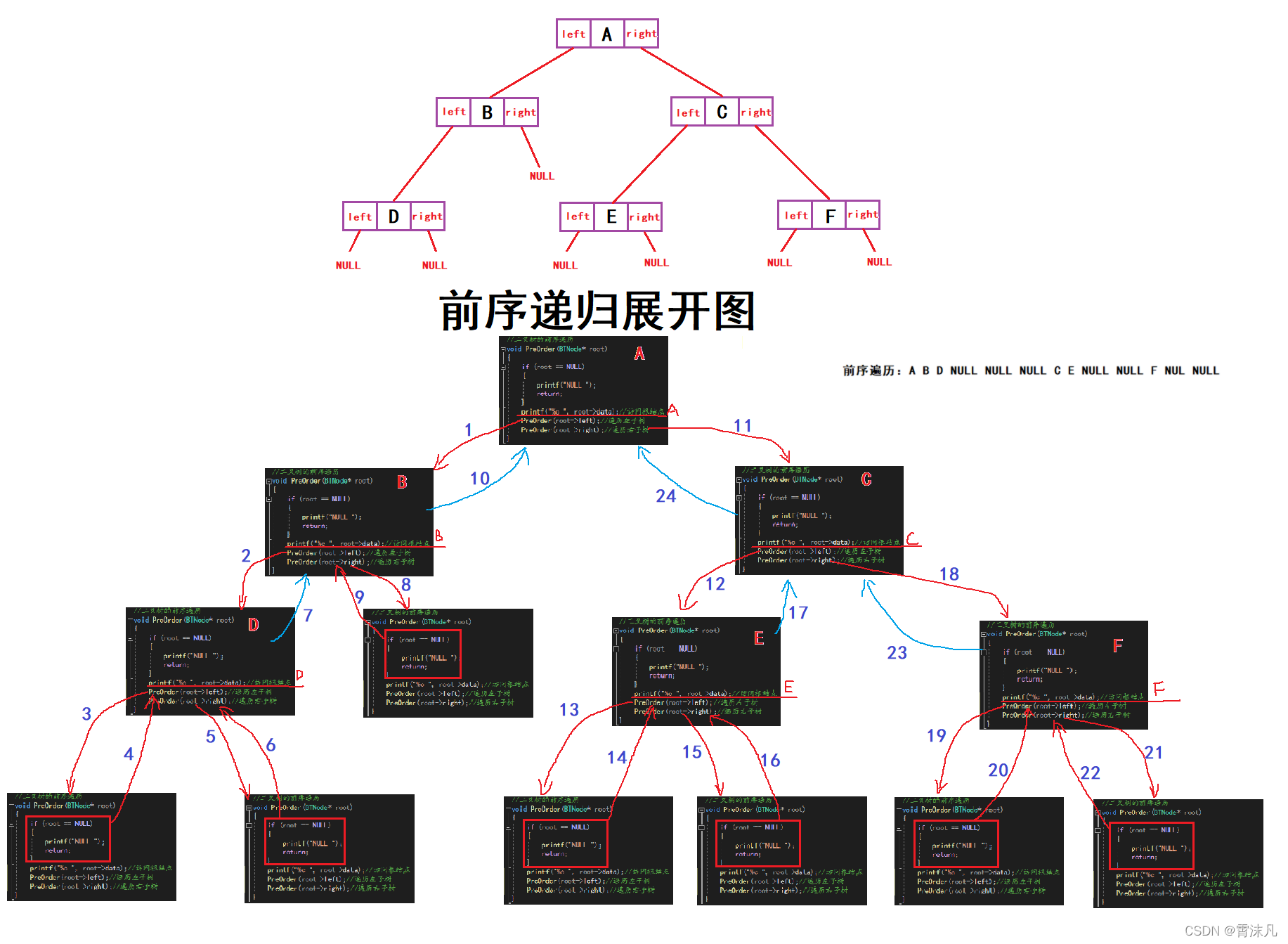
3.二叉树的前序遍历

//二叉树的前序遍历
void PreOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	printf("%c ", root->data);//访问根结点
	PreOrder(root->left);//遍历左子树
	PreOrder(root->right);//遍历右子树
}

4.二叉树的中序遍历 

中序递归原理和前序类似；画图分析即可； 

//二叉树的中序遍历
void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	InOrder(root->left);//遍历左子树
	printf("%c ", root->data);//访问根结点
	InOrder(root->right);//遍历右子树
}

5.二叉树的后续遍历 

后序递归原理和前序类似；画图分析即可；  

//二叉树的后序遍历
void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	PostOrder(root->left);//遍历左子树
	PostOrder(root->right);//遍历右子树
	printf("%c ", root->data);//访问根结点
}

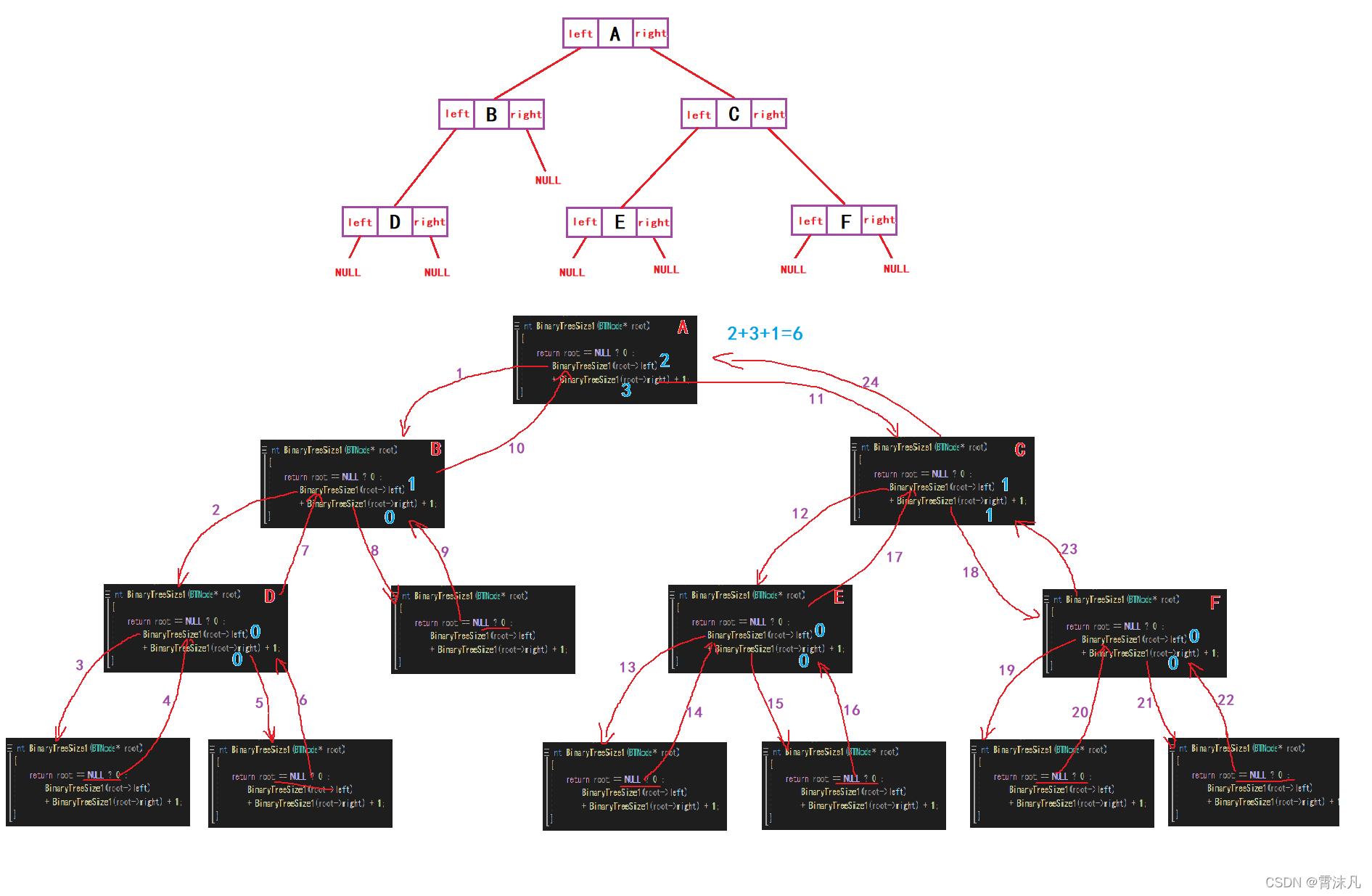
6.二叉树的结点个数 

思路:：遍历左子树的结点个数+遍历右子树的结点个数；

//方法一（最优）
int BinaryTreeSize1(BTNode* root)
{
	return root == NULL ? 0 : BinaryTreeSize1(root->left) + BinaryTreeSize1(root->right) + 1;
}

//方法二
void BinaryTreeSize2(BTNode* root, int* pn)
{
	if (root == NULL)
	{
		return;
	}
	++(*pn);
	BinaryTreeSize2(root->left, pn);
	BinaryTreeSize2(root->right, pn);
}

7.二叉树叶子结点个数 

 叶子结点：就是度为0的点，我们通过遍历它的左子树和右子树的叶子结点个数并相加；

// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{
    //树为空，没有叶子结点
	if (root == NULL)
	{
		return 0;
	}
    //只有一个节点，说明只有一个叶子结点
	if (root->left == NULL && root->right == NULL)
	{
		return 1;
	}
    //上述两种情况都存在，就去遍历左子树和右子树
	return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}

8.二叉树第k层的结点给个数

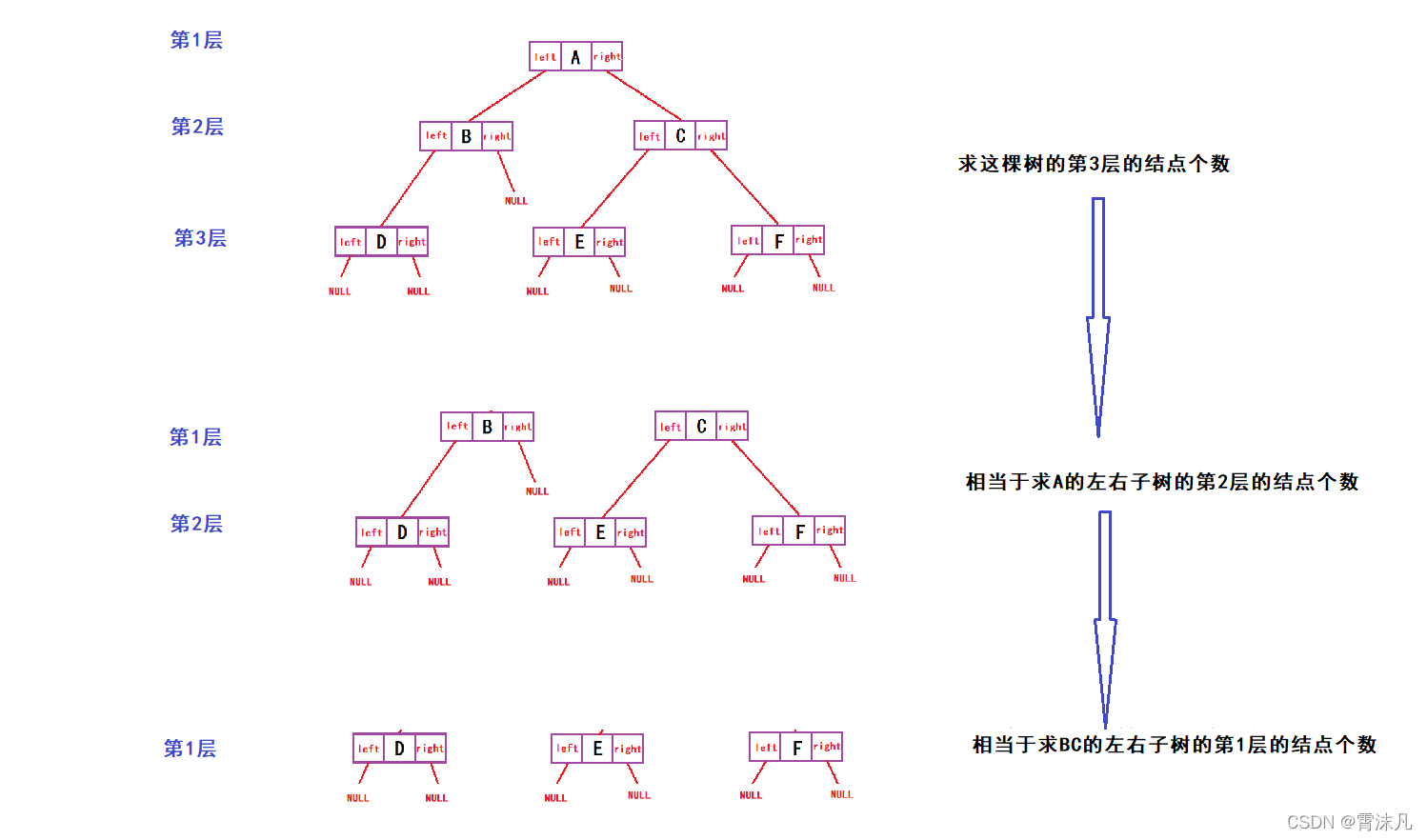
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{
	assert(k >= 1);
	if (root == NULL)
	{
		return 0;
	}
	if (k == 1)
	{
		return 1;
	}
	//root不等于空，k也不等于1，说明root这棵树的第k节点在字树里面
	//转换成求左右子树的第k-1的节点数量；
	return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}

9.二叉树的深度/高度 

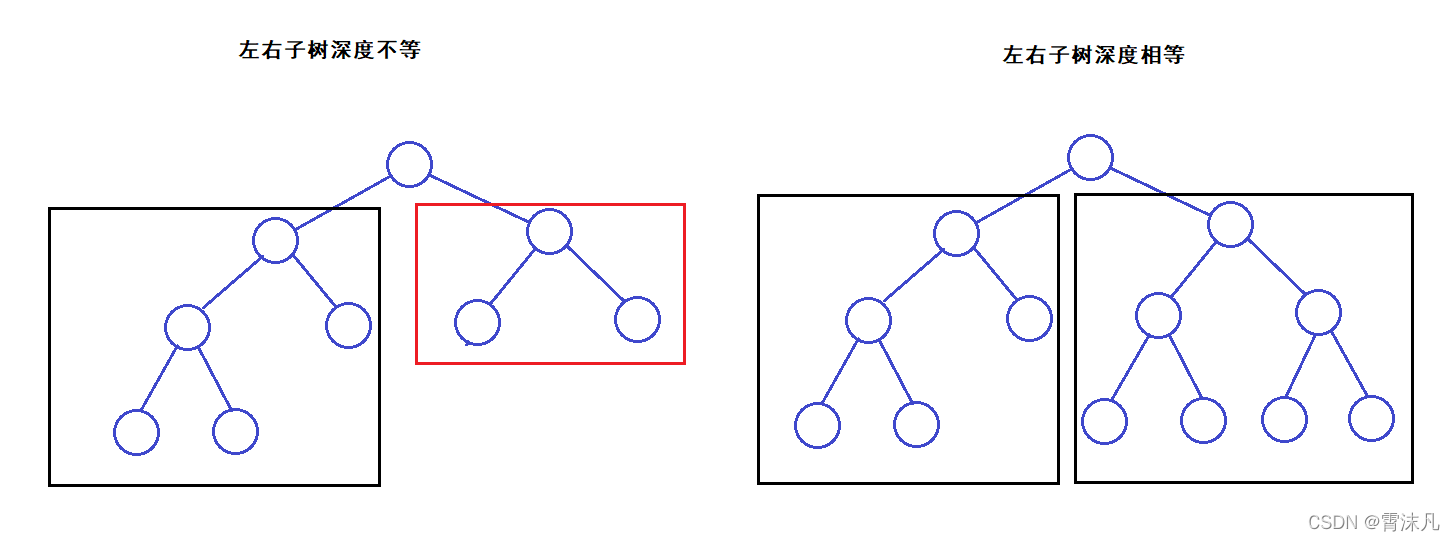
利用递归的思想，去遍历左右子树，存在两种可能（非空树的情况），递归以后，左右子树深度相等 或者不相等（左深或右深）；

//二叉树深度/高度
int BinaryTreeDepth(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	int leftDepth = BinaryTreeDepth(root->left);//算出左子树的深度
	int rightDepth = BinaryTreeDepth(root->right);//算出右子树的深度
	return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;//谁大加1
}

10.二叉树查找值为x的节点 

// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
    //如果树为空，则找不到
	if (root == NULL)
	{
		return NULL;
	}
    //根节点与找的值相等
	if (root->data == x)
	{
		return root;
	}
    //遍历左子树去找
	BTNode* leftret = BinaryTreeFind(root->left, x);
    //左子树找完都没有，加个判断，让其返回去右子树找
	if (leftret)
	{
		return leftret;
	}
    //遍历右子树去找
	BTNode* rightret = BinaryTreeFind(root->right, x);
    //右子树找完都没有
	if (rightret)
	{
		return rightret;
	}
    //到这里就找不到了
	return NULL;
}

11.二叉树层序遍历 

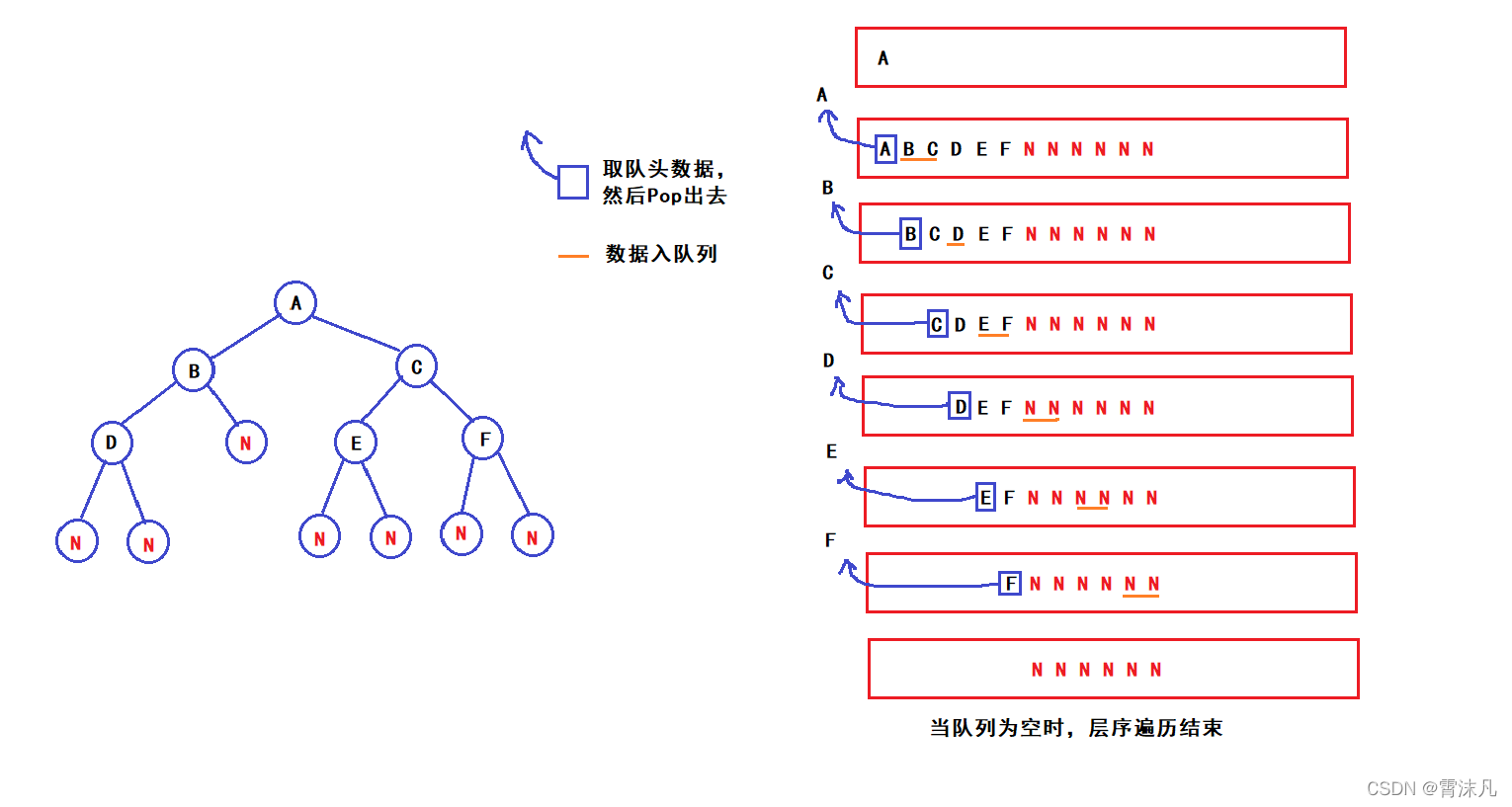
层序遍历：从上至下，从左至右；和队列的特点一样，先进先出；

思路： 先入二叉树的根节点，然后Pop出去，再入根节点的左右孩子，每次Pop一个节点，其孩子入队列；

这里我们用到了队列，队列和二叉树如何联系起来呢？

//Queue.h
struct BinaryTreeNode;//前置声明

typedef struct BinaryTreeNode* QDataType;
typedef struct QueueNode
{
	struct QueueNode* next;
	QDataType data;
}QueueNode;

typedef struct Queue
{
	QueueNode* head;
	QueueNode* tail;
}Queue;

/***************************************************************/
//test.c
typedef char BTDataType;
typedef struct BinaryTreeNode
{
	BTDataType data;//结点
	struct BinaryTreeNode* left;//左子树
	struct BinaryTreeNode* right;//右子树
}BTNode;

原来使用队列的时候我们是让其存储的整形数据，我们这里将其设计为存储二叉树节点的指针；

// 层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}
	Queue q;
	QueueInit(&q);
	QueuePush(&q, root);
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		printf("%c ", front->data);
		//孩子带进队列
		if (front->left)
		{
			QueuePush(&q, front->left);
		}
		if (front->right)
		{
			QueuePush(&q, front->right);
		}
	}
	printf("\n");
	QueueDestroy(&q);
}

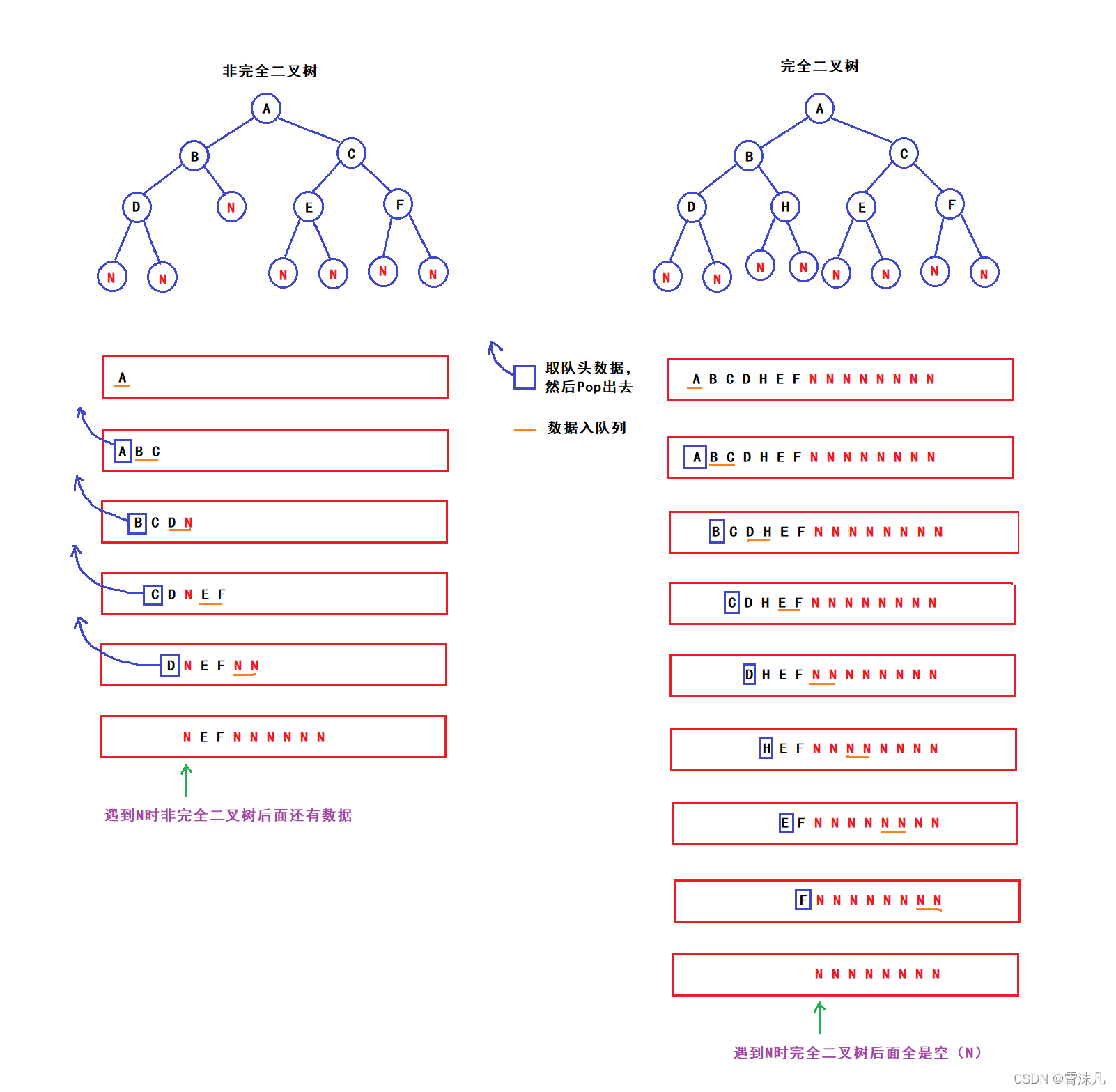
12.判断是否为完全二叉树 

 

//判断一棵二叉树是不是完全二叉树
bool BinaryTreeComplete(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	QueuePush(&q, root);
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		//孩子带进队列
		if (front == NULL)
		{
			break;
		}
		else
		{
			QueuePush(&q, front->left);
			QueuePush(&q, front->right);
		}
	}
	//遇到空以后，检查队列中剩下的节点
	//1.剩下的全是空，则是完全二叉树
	//2.剩下的是非空，则不是完全二叉树
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		if (front != NULL)
		{
			QueueDestroy(&q);
			return false;
		}
	}
	QueueDestroy(&q);
	return true;
}

13.二叉树的销毁 

// 二叉树销毁(用后序的方式来释放)
void BinaryTreeDestory(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}
	BinaryTreeDestory(root->left);
	BinaryTreeDestory(root->right);
	free(root);
}

三、源代码 

Queue.h 

#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <stdbool.h>

struct BinaryTreeNode;//前置声明

typedef struct BinaryTreeNode* QDataType;
typedef struct QueueNode
{
	struct QueueNode* next;
	QDataType data;
}QueueNode;

typedef struct Queue
{
	QueueNode* head;
	QueueNode* tail;
}Queue;

//队列的初始化
void QueueInit(Queue* pq);

//队列的销毁
void QueueDestroy(Queue* pq);

//队尾入队列
void QueuePush(Queue* pq, QDataType x);

//队头出队列
void QueuePop(Queue* pq);

//取队头的数据
QDataType QueueFront(Queue* pq);

//取队尾的数据
QDataType QueueBack(Queue* pq);

//计算有多少个数据
int QueueSize(Queue* pq);

//判断队列是否为空
bool QueueEmpty(Queue* pq);

Queue.c 

#include "Queue.h"

//队列的初始化
void QueueInit(Queue* pq)
{
	assert(pq);
	pq->head = NULL;
	pq->tail = NULL;
}

//队列的销毁
void QueueDestroy(Queue* pq)
{
	assert(pq);
	QueueNode* cur = pq->head;
	while (cur != NULL)
	{
		QueueNode* next = cur->next;
		free(cur);
		cur = next;
	}
	pq->head = pq->tail = NULL;
}

//队尾入队列
void QueuePush(Queue* pq, QDataType x)
{
	assert(pq);
	QueueNode* newnode = (QueueNode*)malloc(sizeof(QueueNode));
	newnode->data = x;
	newnode->next = NULL;
	if (pq->head == NULL)
	{
		pq->head = pq->tail = newnode;
	}
	else
	{
		pq->tail->next = newnode;
		pq->tail = newnode;
	}
}

//队头出队列
void QueuePop(Queue* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));
	QueueNode* next = pq->head->next;
	free(pq->head);
	pq->head = next;

	//此时head和tail同时指向最后一个空间，释放head后，要注意也要把tail释放了
	if (pq->head == NULL)
	{
		pq->tail = NULL;
	}
}

//取队头的数据
QDataType QueueFront(Queue* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));
	return pq->head->data;
}

//取队尾的数据
QDataType QueueBack(Queue* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));
	return pq->tail->data;
}

//计算有多少个数据
int QueueSize(Queue* pq)
{
	assert(pq);
	int n = 0;
	QueueNode* cur = pq->head;
	while (cur)
	{
		++n;
		cur = cur->next;
	}
	return n;
}

//判断队列是否为空
bool QueueEmpty(Queue* pq)
{
	assert(pq);
	return pq->head == NULL;
}

test.c

#include "Queue.h"

typedef char BTDataType;
typedef struct BinaryTreeNode
{
	BTDataType data;//结点
	struct BinaryTreeNode* left;//左子树
	struct BinaryTreeNode* right;//右子树
}BTNode;
//二叉树的初始化
BTNode* BuyNode(BTDataType x);

//创建二叉树
BTNode* CreatBinaryTree();

//二叉树的前序遍历
void PreOrder(BTNode* root);

//二叉树的中序遍历
void InOrder(BTNode* root);

//二叉树的后序遍历
void PostOrder(BTNode* root);

//二叉树的结点个数
int BinaryTreeSize1(BTNode* root);
void BinaryTreeSize2(BTNode* root, int* pn);

// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root);

// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k);

//二叉树深度/高度
int BinaryTreeDepth(BTNode* root);

// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);

//二叉树的层序遍历
void BinaryTreeLevelOrder(BTNode* root);

//判断是都为完全二叉树
bool BinaryTreeComplete(BTNode* root);

// 二叉树销毁
void BinaryTreeDestory(BTNode* root);

/*************************************************************************************/
//二叉树的初始化
BTNode* BuyNode(BTDataType x)
{
	BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
	if (newnode == NULL)
	{
		printf("malloc fail\n");
		exit(-1);
	}
	newnode->data = x;
	newnode->left = newnode->right = NULL;
	return newnode;
}

//创建二叉树
BTNode* CreatBinaryTree()
{
	BTNode* nodeA = BuyNode('A');
	BTNode* nodeB = BuyNode('B');
	BTNode* nodeC = BuyNode('C');
	BTNode* nodeD = BuyNode('D');
	BTNode* nodeE = BuyNode('E');
	BTNode* nodeF = BuyNode('F');

	nodeA->left = nodeB;
	nodeA->right = nodeC;
	nodeB->left = nodeD;
	nodeC->left = nodeE;
	nodeC->right = nodeF;
	return nodeA;
}

//二叉树的前序遍历
void PreOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	printf("%c ", root->data);//访问根结点
	PreOrder(root->left);//遍历左子树
	PreOrder(root->right);//遍历右子树
}

//二叉树的中序遍历
void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	InOrder(root->left);//遍历左子树
	printf("%c ", root->data);//访问根结点
	InOrder(root->right);//遍历右子树
}

//二叉树的后序遍历
void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	PostOrder(root->left);//遍历左子树
	PostOrder(root->right);//遍历右子树
	printf("%c ", root->data);//访问根结点
}

//二叉树的结点个数
/*******************************************************/
//方法一（最优）
int BinaryTreeSize1(BTNode* root)
{
	return root == NULL ? 0 : 
		BinaryTreeSize1(root->left) 
		+ BinaryTreeSize1(root->right) + 1;
}

//方法二
void BinaryTreeSize2(BTNode* root, int* pn)
{
	if (root == NULL)
	{
		return;
	}
	++(*pn);
	BinaryTreeSize2(root->left, pn);
	BinaryTreeSize2(root->right, pn);
}
/*******************************************************/

// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{
	//树为空，没有叶子结点
	if (root == NULL)
	{
		return 0;
	}
	//只有一个节点，说明只有一个叶子结点
	if (root->left == NULL && root->right == NULL)
	{
		return 1;
	}
	//上述两种情况都存在，就去遍历左子树和右子树
	return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}


// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{
	assert(k >= 1);
	if (root == NULL)
	{
		return 0;
	}
	if (k == 1)
	{
		return 1;
	}
	//root不等于空，k也不等于1，说明root这棵树的第k节点在字树里面
	//转换成求左右子树的第k-1的节点数量；
	return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}

//二叉树深度/高度
int BinaryTreeDepth(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	int leftDepth = BinaryTreeDepth(root->left);
	int rightDepth = BinaryTreeDepth(root->right);
	return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;
}

// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
	//如果树为空，则找不到
	if (root == NULL)
	{
		return NULL;
	}
	//根节点与找的值相等
	if (root->data == x)
	{
		return root;
	}
	//遍历左子树去找
	BTNode* leftret = BinaryTreeFind(root->left, x);
	//左子树找完都没有，加个判断，让其返回去右子树找
	if (leftret)
	{
		return leftret;
	}
	//遍历右子树去找
	BTNode* rightret = BinaryTreeFind(root->right, x);
	//右子树找完都没有
	if (rightret)
	{
		return rightret;
	}
	//到这里就找不到了
	return NULL;
}

// 层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}
	Queue q;
	QueueInit(&q);
	QueuePush(&q, root);
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		printf("%c ", front->data);
		//孩子带进队列
		if (front->left)
		{
			QueuePush(&q, front->left);
		}
		if (front->right)
		{
			QueuePush(&q, front->right);
		}
	}
	printf("\n");
	QueueDestroy(&q);
}

//判断一棵二叉树是不是完全二叉树
bool BinaryTreeComplete(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	QueuePush(&q, root);
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		//孩子带进队列
		if (front == NULL)
		{
			break;
		}
		else
		{
			QueuePush(&q, front->left);
			QueuePush(&q, front->right);
		}
	}
	//遇到空以后，检查队列中剩下的节点
	//1.剩下的全是空，则是完全二叉树
	//2.剩下的是非空，则不是完全二叉树
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		if (front != NULL)
		{
			QueueDestroy(&q);
			return false;
		}
	}
	QueueDestroy(&q);
	return true;
}

// 二叉树销毁
void BinaryTreeDestory(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}
	BinaryTreeDestory(root->left);
	BinaryTreeDestory(root->right);
	free(root);
}

int main()
{
	BTNode* root = CreatBinaryTree();

	printf("前序遍历：");
	PreOrder(root);
	printf("\n\n");

	printf("中序遍历：");
	InOrder(root);
	printf("\n\n");

	printf("后序遍历：");
	PostOrder(root);
	printf("\n\n");

	printf("二叉树节点个数,方法1：");
	printf("%d\n\n", BinaryTreeSize1(root));

	printf("二叉树节点个数,方法2：");
	int n = 0;
	BinaryTreeSize2(root, &n);
	printf("%d\n\n", n);

	printf("二叉树叶子节点个数：");
	printf("%d\n\n", BinaryTreeLeafSize(root));

	printf("二叉树第3层节点个数：");
	int k = 3;
	printf("%d\n\n", BinaryTreeLevelKSize(root, k));

	printf("二叉树深度:");
	printf("%d\n\n", BinaryTreeDepth(root));

	printf("二叉树C结点前序遍历:");
	BTNode* cur = BinaryTreeFind(root, 'C');
	PreOrder(cur);
	printf("\n\n");

	printf("层序遍历：");
	BinaryTreeLevelOrder(root);
	printf("\n");

	printf("是否为完全二叉树0/1：");
	printf("%d\n", BinaryTreeComplete(root));

	BinaryTreeDestory(root);
	root = NULL;

	return 0;
}

运行效果 

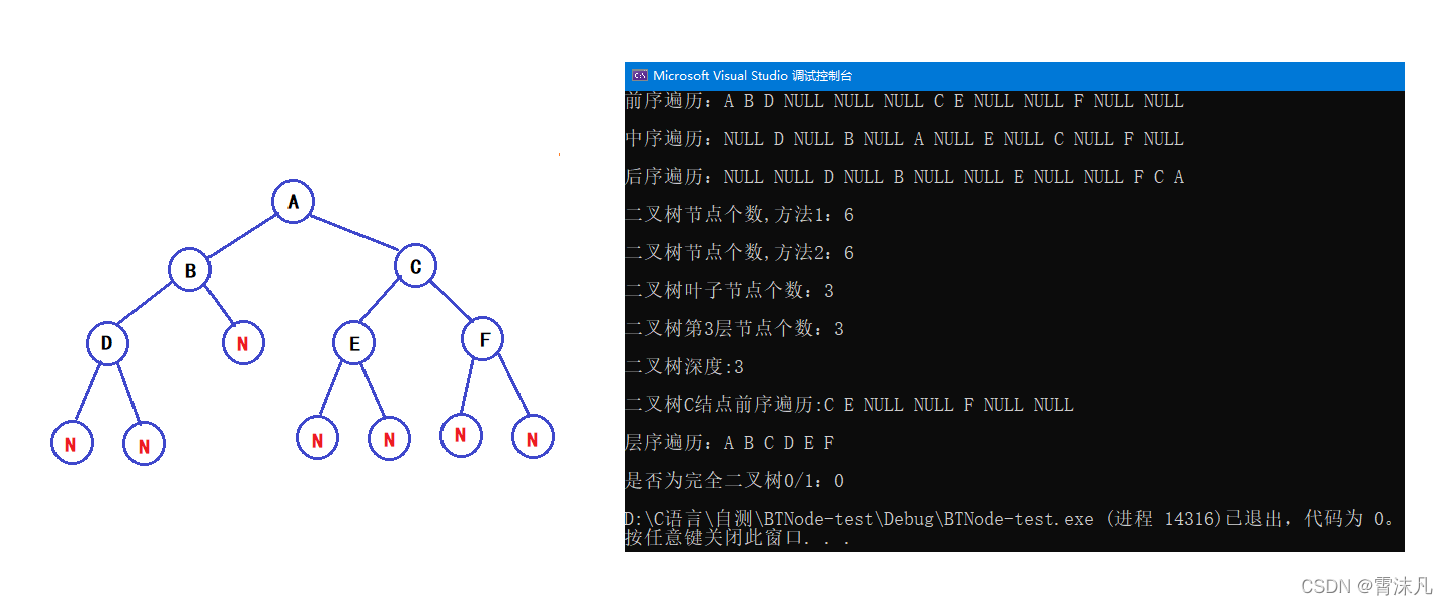
二叉树链式结构的实现主要是递归思想，加上队列的混合使用，不熟悉的小伙伴可以去看这里

数据结构（初阶）——栈和队列②https://blog.csdn.net/sjsjnsjnn/article/details/124086038?spm=1001.2014.3001.5501

想要熟练掌握，需要小伙伴亲自画图分析理解，并自行编写代码实现，查找错误点，仔细分析