此算法应用的面也很广,很值得学习。在电力系统领域也是特别棒的:
目录

1 蚂蚁狮子概述(ALO)
蚁狮或所谓的涂鸦虫是蚁蛉科家族的成员,属于神经翅目(网翅昆虫)。蚁狮的生命有两个关键阶段:幼虫和成虫。成年期仅持续 3-5 周,用于繁殖。另一方面,生命周期的延长阶段,即幼虫阶段,大部分用于猎杀他们最喜欢的猎物,即蚂蚁。蚁狮幼虫的狩猎行为独特而迷人。如图1所示,是蚂蚁狮子和它的狩猎机制。

它们沿着圆形路径移动,并用它们巨大的下颚扔出沙子,在沙质土壤中形成小的(1-3 英寸长)漏斗形坑,如图2所示,以诱捕蚂蚁。

他们躲在坑底下,等待蚂蚁或小昆虫被困。漏斗形坑的边缘非常锋利,小昆虫无法逃脱,很容易掉到陷阱底部,如图3所示。蚁狮还不断将沙子扔向陷阱的外缘,以阻止猎物的任何逃跑尝试。

最后,昆虫滑入坑底,被拉到土壤下并被蚁狮吃掉。猎物的残骸被扔到坑外。之后,蚁狮为后续的目标猎物修改坑。蚁狮的饥饿程度越高,它们挖的陷阱就越大。通过这种方式,蚁狮已经进化和调整,以提高它们的生存前景。
2 数学建模
2.1 蚂蚁的随机游走
对于这种可随机修改的问题,找到最佳算法是一项具有挑战性的任务。 蚂蚁在优化的每一步都会以任意行走的方式改变它们的位置,数学上可表示为式(2-1):

式中:X(t)为蚂蚁的随机游走步数集; cumsum表示计算累加和;k为随机游走的步数(本文取为最大迭代次数);而r(t)为一个随机函数,定义为:

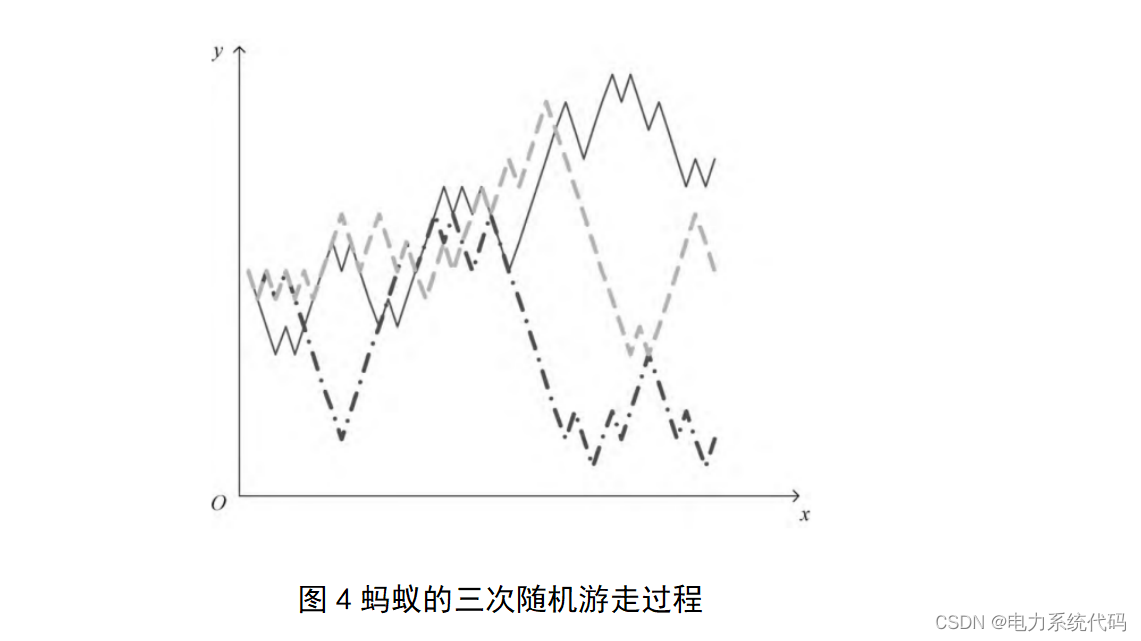
式中:rand为[0,1]上均匀分布的随机数。图4模拟了蚂蚁的三次随机游走过程(h取50),可以看出随机游走过程有较强的搜索能力。
鉴于每个搜索空间都是有限的,即有一个边界,所以出于这个原因,蚂蚁的任意行走被限制在搜索空间的边界内,使用最小—-最大归一化,如式(2-3):
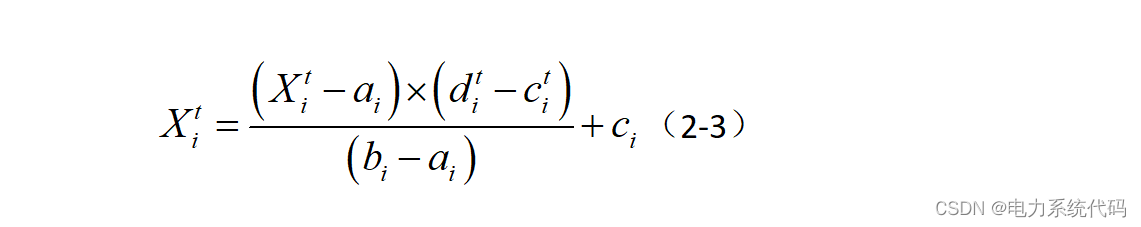
式中: 为第
维变量随机游走的最小值;
为第
维变量随机游走的最大值;
为第
维变量在第代的最小值;
为第
维变量在第代的最大值。
2.2蚁狮的陷阱蚂蚁的影响
蚂蚁在随机游走过程中其行动会受到蚁狮陷阱的影响,数学上表示为:
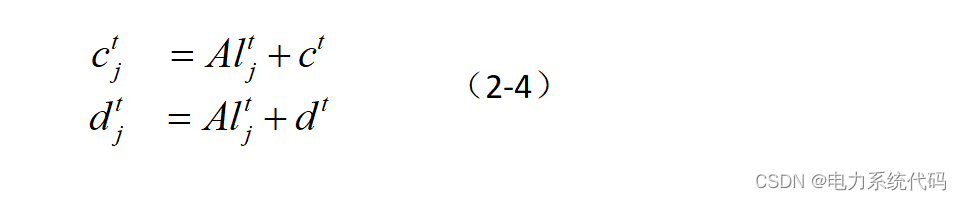
式中:为所有变量在第
代的最小值;
为所有变量在第
代的最大值;
是第
只蚂蚁在第代的最小值;
是第
只蚂蚁在第代的最大值;
为第
只蚂蚁选择的相应的蚁狮在第
代的位置。
2.3 蚂蚁掉入陷阱,蚁狮的捕食
每只蚂蚁只能被一只蚁狮捕获,某只蚂蚁具体要被哪只蚁狮捕获是通过轮盘赌(RouletteWheel)策略来选择的,适应度越高的蚁狮有着更高的捕获蚂蚁的机会。另外,蚁狮可以构造陷阱,蚂蚁一旦落入陷阱,蚁狮就会向外扬沙以使蚂蚁不至于逃脱,这时蚂蚁随机游走的范围将急剧缩小。数学上表示为:

式中:是比例系数;为最大迭代次数;
为一随迭代次数增大的数.
2.4 位置更新
当某只蚂蚁的适应度变得高于蚁狮时﹐即认为其被蚁狮捕获,此时蚁狮会根据蚂蚁的位置来更新其位置,表示为:
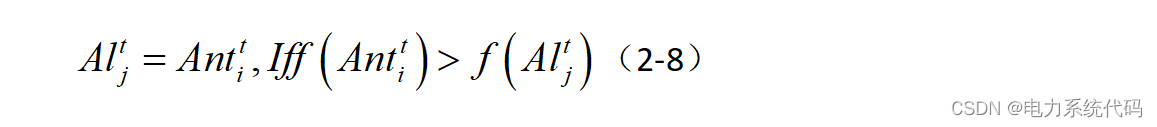
式中:为第
只蚂蚁在第
代的位置;
为适应度函数。
2.5 精英策略
每一次迭代获得的适应度最好的蚁狮被认为是精英蚁狮。精英蚁狮将影响所有蚂蚁的行动。第t只蚂蚁在第t +1代的位置由下式确定:
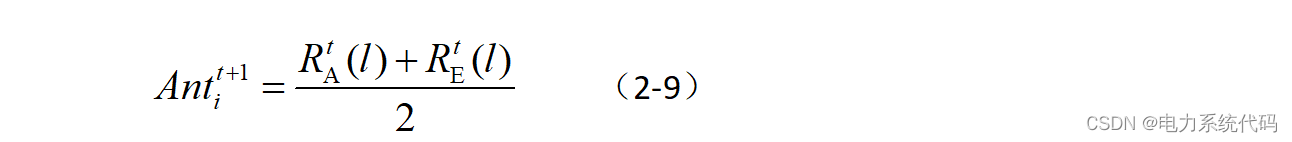
式中:为蚂蚁在一只由轮盘赌在第
代选择到的蚁狮附近随机游走第
步产生的值;
为在第
代的精英蚁狮周围的随机游走第
步产生的值。可以取随机游走步数内的任何值,本文取
。
3 完整Matlab代码实现
3.1 Matlab代码
%% 蚂蚁狮子优化算法(ALO)
%%======欢迎关注公众号:电力系统与算法之美===========
clear all
clc
SearchAgents_no=40;
Function_name='F1'; % 可以切换F1到F23的测试函数的名称 (也可以换成自己的目标函数)
Max_iteration=500; % 最大迭代次数
%% 所选基准函数详细情况
[lb,ub,dim,fobj]=Get_Functions_details(Function_name);
[Best_score,Best_pos,cg_curve]=ALO(SearchAgents_no,Max_iteration,lb,ub,dim,fobj);
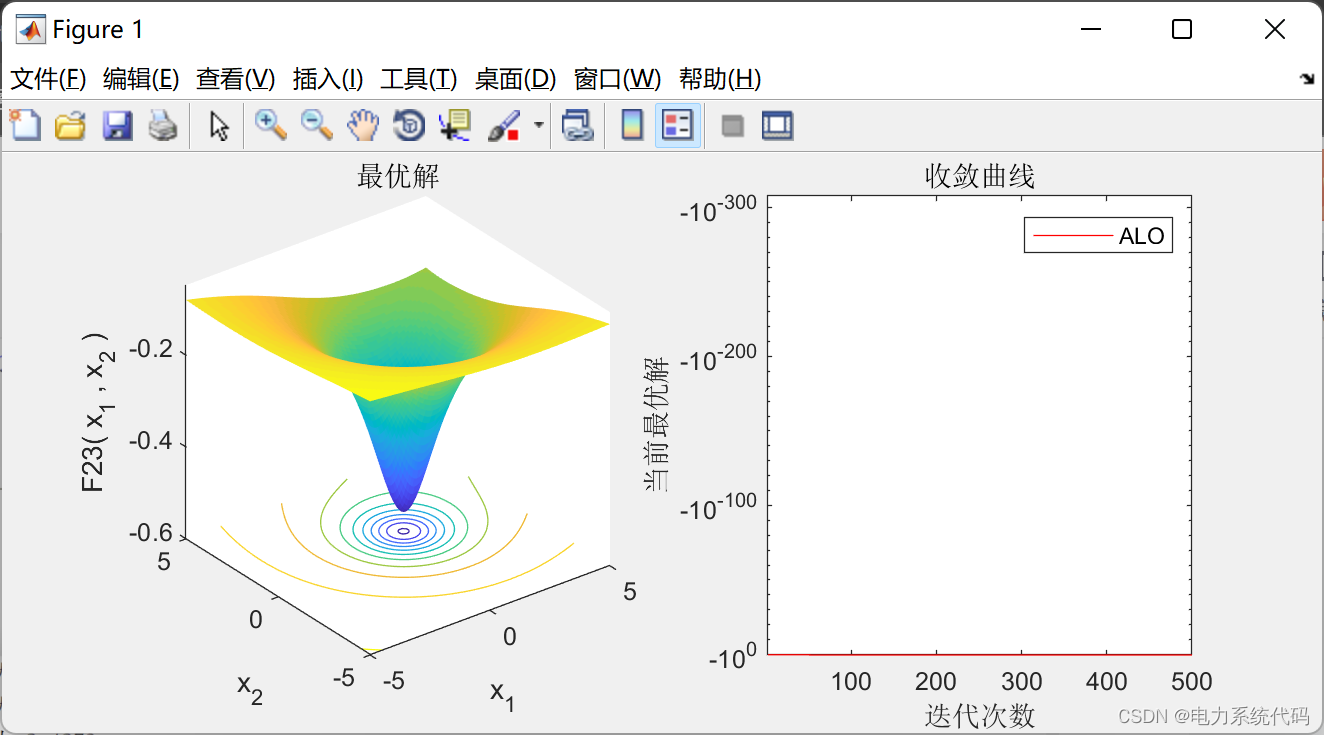
figure('Position',[500 500 660 290])
%% 绘制搜索空间
subplot(1,2,1);
func_plot(Function_name);
title('最优解')
xlabel('x_1');
ylabel('x_2');
zlabel([Function_name,'( x_1 , x_2 )'])
grid off
%% 绘制目标空间
subplot(1,2,2);
semilogy(cg_curve,'Color','r')
title('收敛曲线')
xlabel('迭代次数');
ylabel('当前最优解');
axis tight
grid off
box on
legend('ALO')
display(['由蚁狮取得的最佳解为 : ', num2str(Best_pos)]);
display(['ALO算法找到的目标函数的最优值是 : ', num2str(Best_score)]);
function [Elite_antlion_fitness,Elite_antlion_position,Convergence_curve]=ALO(N,Max_iter,lb,ub,dim,fobj)
%% 初始化蚁狮和蚂蚁的位置
antlion_position=initialization(N,dim,ub,lb);
ant_position=initialization(N,dim,ub,lb);
%% 初始化变量以保存精英位置、蚂蚁狮子排序、收敛曲线、蚁狮适应度和蚂蚁适应度
Sorted_antlions=zeros(N,dim);
Elite_antlion_position=zeros(1,dim);
Elite_antlion_fitness=inf;
Convergence_curve=zeros(1,Max_iter);
antlions_fitness=zeros(1,N);
ants_fitness=zeros(1,N);
%% 计算初始蚁狮的适应度并进行排序
for i=1:size(antlion_position,1)
antlions_fitness(1,i)=fobj(antlion_position(i,:));
end
[sorted_antlion_fitness,sorted_indexes]=sort(antlions_fitness);
for newindex=1:N
Sorted_antlions(newindex,:)=antlion_position(sorted_indexes(newindex),:);
end
Elite_antlion_position=Sorted_antlions(1,:);
Elite_antlion_fitness=sorted_antlion_fitness(1);
%% 主循环从第二轮迭代开始,因为第一轮迭代专门用于计算蚁狮的适应度
Current_iter=2;
while Current_iter<Max_iter+1
%=====模拟蚂蚁随机游走===========
for i=1:size(ant_position,1)
%根据它们的适合度选择蚂蚁狮子( 蚁狮越好捕获蚂蚁的几率越高 )
Rolette_index=RouletteWheelSelection(1./sorted_antlion_fitness);
if Rolette_index==-1
Rolette_index=1;
end
%=====RA通过轮盘赌围绕选定的蚁狮随机游走========
RA=Random_walk_around_antlion(dim,Max_iter,lb,ub, Sorted_antlions(Rolette_index,:),Current_iter);
%====RA是围绕精英的随机游走( 迄今为止最好的蚂蚁 )======
[RE]=Random_walk_around_antlion(dim,Max_iter,lb,ub, Elite_antlion_position(1,:),Current_iter);
ant_position(i,:)= (RA(Current_iter,:)+RE(Current_iter,:))/2;
end
for i=1:size(ant_position,1)
%边界检查(走到边界的话,带回搜索空间内)
Flag4ub=ant_position(i,:)>ub;
Flag4lb=ant_position(i,:)<lb;
ant_position(i,:)=(ant_position(i,:).*(~(Flag4ub+Flag4lb)))+ub.*Flag4ub+lb.*Flag4lb;
ants_fitness(1,i)=fobj(ant_position(i,:));
end
%根据蚂蚁更新蚂蚁的位置和适应度(如果蚂蚁变得比蚂蚁更适合,
%我们假设它被蚂蚁咳嗽,蚂蚁更新到它的位置构建陷阱)。
double_population=[Sorted_antlions;ant_position];
double_fitness=[sorted_antlion_fitness ants_fitness];
[double_fitness_sorted I]=sort(double_fitness);
double_sorted_population=double_population(I,:);
antlions_fitness=double_fitness_sorted(1:N);
Sorted_antlions=double_sorted_population(1:N,:);
% 如果任何蚁群变得比它更适合,则更新精英的位置
if antlions_fitness(1)<Elite_antlion_fitness
Elite_antlion_position=Sorted_antlions(1,:);
Elite_antlion_fitness=antlions_fitness(1);
end
%=====保留种群中的精英=============
Sorted_antlions(1,:)=Elite_antlion_position;
antlions_fitness(1)=Elite_antlion_fitness;
%=====更新收敛曲线==================
Convergence_curve(Current_iter)=Elite_antlion_fitness;
%===显示迄今为止得到的迭代和最佳最优=====
if mod(Current_iter,50)==0
display(['迭代 ', num2str(Current_iter), ' 次,精英最优解为', num2str(Elite_antlion_fitness)]);
end
Current_iter=Current_iter+1;
end
%=====目标函数可视化===================
function func_plot(func_name)
[lb,ub,dim,fobj]=Get_Functions_details(func_name);
switch func_name
case 'F1'
x=-100:2:100; y=x; %[-100,100]
case 'F2'
x=-100:2:100; y=x; %[-10,10]
case 'F3'
x=-100:2:100; y=x; %[-100,100]
case 'F4'
x=-100:2:100; y=x; %[-100,100]
case 'F5'
x=-200:2:200; y=x; %[-5,5]
case 'F6'
x=-100:2:100; y=x; %[-100,100]
case 'F7'
x=-1:0.03:1; y=x %[-1,1]
case 'F8'
x=-500:10:500;y=x; %[-500,500]
case 'F9'
x=-5:0.1:5; y=x; %[-5,5]
case 'F10'
x=-20:0.5:20; y=x;%[-500,500]
case 'F11'
x=-500:10:500; y=x;%[-0.5,0.5]
case 'F12'
x=-10:0.1:10; y=x;%[-pi,pi]
case 'F13'
x=-5:0.08:5; y=x;%[-3,1]
case 'F14'
x=-100:2:100; y=x;%[-100,100]
case 'F15'
x=-5:0.1:5; y=x;%[-5,5]
case 'F16'
x=-1:0.01:1; y=x;%[-5,5]
case 'F17'
x=-5:0.1:5; y=x;%[-5,5]
case 'F18'
x=-5:0.06:5; y=x;%[-5,5]
case 'F19'
x=-5:0.1:5; y=x;%[-5,5]
case 'F20'
x=-5:0.1:5; y=x;%[-5,5]
case 'F21'
x=-5:0.1:5; y=x;%[-5,5]
case 'F22'
x=-5:0.1:5; y=x;%[-5,5]
case 'F23'
x=-5:0.1:5; y=x;%[-5,5]
end
L=length(x);
f=[];
for i=1:L
for j=1:L
if strcmp(func_name,'F15')==0 && strcmp(func_name,'F19')==0 && strcmp(func_name,'F20')==0 && strcmp(func_name,'F21')==0 && strcmp(func_name,'F22')==0 && strcmp(func_name,'F23')==0
f(i,j)=fobj([x(i),y(j)]);
end
if strcmp(func_name,'F15')==1
f(i,j)=fobj([x(i),y(j),0,0]);
end
if strcmp(func_name,'F19')==1
f(i,j)=fobj([x(i),y(j),0]);
end
if strcmp(func_name,'F20')==1
f(i,j)=fobj([x(i),y(j),0,0,0,0]);
end
if strcmp(func_name,'F21')==1 || strcmp(func_name,'F22')==1 ||strcmp(func_name,'F23')==1
f(i,j)=fobj([x(i),y(j),0,0]);
end
end
end
surfc(x,y,f,'LineStyle','none');
end%=======目标函数=================
function [lb,ub,dim,fobj] = Get_Functions_details(F)
switch F
case 'F1'
fobj = @F1;
lb=-100;
ub=100;
dim=10;
case 'F2'
fobj = @F2;
lb=-10;
ub=10;
dim=10;
case 'F3'
fobj = @F3;
lb=-100;
ub=100;
dim=10;
case 'F4'
fobj = @F4;
lb=-100;
ub=100;
dim=10;
case 'F5'
fobj = @F5;
lb=-30;
ub=30;
dim=10;
case 'F6'
fobj = @F6;
lb=-100;
ub=100;
dim=10;
case 'F7'
fobj = @F7;
lb=-1.28;
ub=1.28;
dim=10;
case 'F8'
fobj = @F8;
lb=-500;
ub=500;
dim=10;
case 'F9'
fobj = @F9;
lb=-5.12;
ub=5.12;
dim=10;
case 'F10'
fobj = @F10;
lb=-32;
ub=32;
dim=10;
case 'F11'
fobj = @F11;
lb=-600;
ub=600;
dim=10;
case 'F12'
fobj = @F12;
lb=-50;
ub=50;
dim=10;
case 'F13'
fobj = @F13;
lb=-50;
ub=50;
dim=10;
case 'F14'
fobj = @F14;
lb=-65.536;
ub=65.536;
dim=2;
case 'F15'
fobj = @F15;
lb=-5;
ub=5;
dim=4;
case 'F16'
fobj = @F16;
lb=-5;
ub=5;
dim=2;
case 'F17'
fobj = @F17;
lb=[-5,0];
ub=[10,15];
dim=2;
case 'F18'
fobj = @F18;
lb=-2;
ub=2;
dim=2;
case 'F19'
fobj = @F19;
lb=0;
ub=1;
dim=3;
case 'F20'
fobj = @F20;
lb=0;
ub=1;
dim=6;
case 'F21'
fobj = @F21;
lb=0;
ub=10;
dim=4;
case 'F22'
fobj = @F22;
lb=0;
ub=10;
dim=4;
case 'F23'
fobj = @F23;
lb=0;
ub=10;
dim=4;
end
end
% F1
function o = F1(x)
o=sum(x.^2);
end
% F2
function o = F2(x)
o=sum(abs(x))+prod(abs(x));
end
% F3
function o = F3(x)
dim=size(x,2);
o=0;
for i=1:dim
o=o+sum(x(1:i))^2;
end
end
% F4
function o = F4(x)
o=max(abs(x));
end
% F5
function o = F5(x)
dim=size(x,2);
o=sum(100*(x(2:dim)-(x(1:dim-1).^2)).^2+(x(1:dim-1)-1).^2);
end
% F6
function o = F6(x)
o=sum(abs((x+.5)).^2);
end
% F7
function o = F7(x)
dim=size(x,2);
o=sum([1:dim].*(x.^4))+rand;
end
% F8
function o = F8(x)
o=sum(-x.*sin(sqrt(abs(x))));
end
% F9
function o = F9(x)
dim=size(x,2);
o=sum(x.^2-10*cos(2*pi.*x))+10*dim;
end
% F10
function o = F10(x)
dim=size(x,2);
o=-20*exp(-.2*sqrt(sum(x.^2)/dim))-exp(sum(cos(2*pi.*x))/dim)+20+exp(1);
end
% F11
function o = F11(x)
dim=size(x,2);
o=sum(x.^2)/4000-prod(cos(x./sqrt([1:dim])))+1;
end
% F12
function o = F12(x)
dim=size(x,2);
o=(pi/dim)*(10*((sin(pi*(1+(x(1)+1)/4)))^2)+sum((((x(1:dim-1)+1)./4).^2).*...
(1+10.*((sin(pi.*(1+(x(2:dim)+1)./4)))).^2))+((x(dim)+1)/4)^2)+sum(Ufun(x,10,100,4));
end
% F13
function o = F13(x)
dim=size(x,2);
o=.1*((sin(3*pi*x(1)))^2+sum((x(1:dim-1)-1).^2.*(1+(sin(3.*pi.*x(2:dim))).^2))+...
((x(dim)-1)^2)*(1+(sin(2*pi*x(dim)))^2))+sum(Ufun(x,5,100,4));
end
% F14
function o = F14(x)
aS=[-32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32;,...
-32 -32 -32 -32 -32 -16 -16 -16 -16 -16 0 0 0 0 0 16 16 16 16 16 32 32 32 32 32];
for j=1:25
bS(j)=sum((x'-aS(:,j)).^6);
end
o=(1/500+sum(1./([1:25]+bS))).^(-1);
end
% F15
function o = F15(x)
aK=[.1957 .1947 .1735 .16 .0844 .0627 .0456 .0342 .0323 .0235 .0246];
bK=[.25 .5 1 2 4 6 8 10 12 14 16];bK=1./bK;
o=sum((aK-((x(1).*(bK.^2+x(2).*bK))./(bK.^2+x(3).*bK+x(4)))).^2);
end
% F16
function o = F16(x)
o=4*(x(1)^2)-2.1*(x(1)^4)+(x(1)^6)/3+x(1)*x(2)-4*(x(2)^2)+4*(x(2)^4);
end
% F17
function o = F17(x)
o=(x(2)-(x(1)^2)*5.1/(4*(pi^2))+5/pi*x(1)-6)^2+10*(1-1/(8*pi))*cos(x(1))+10;
end
% F18
function o = F18(x)
o=(1+(x(1)+x(2)+1)^2*(19-14*x(1)+3*(x(1)^2)-14*x(2)+6*x(1)*x(2)+3*x(2)^2))*...
(30+(2*x(1)-3*x(2))^2*(18-32*x(1)+12*(x(1)^2)+48*x(2)-36*x(1)*x(2)+27*(x(2)^2)));
end
% F19
function o = F19(x)
aH=[3 10 30;.1 10 35;3 10 30;.1 10 35];cH=[1 1.2 3 3.2];
pH=[.3689 .117 .2673;.4699 .4387 .747;.1091 .8732 .5547;.03815 .5743 .8828];
o=0;
for i=1:4
o=o-cH(i)*exp(-(sum(aH(i,:).*((x-pH(i,:)).^2))));
end
end
% F20
function o = F20(x)
aH=[10 3 17 3.5 1.7 8;.05 10 17 .1 8 14;3 3.5 1.7 10 17 8;17 8 .05 10 .1 14];
cH=[1 1.2 3 3.2];
pH=[.1312 .1696 .5569 .0124 .8283 .5886;.2329 .4135 .8307 .3736 .1004 .9991;...
.2348 .1415 .3522 .2883 .3047 .6650;.4047 .8828 .8732 .5743 .1091 .0381];
o=0;
for i=1:4
o=o-cH(i)*exp(-(sum(aH(i,:).*((x-pH(i,:)).^2))));
end
end
% F21
function o = F21(x)
aSH=[4 4 4 4;1 1 1 1;8 8 8 8;6 6 6 6;3 7 3 7;2 9 2 9;5 5 3 3;8 1 8 1;6 2 6 2;7 3.6 7 3.6];
cSH=[.1 .2 .2 .4 .4 .6 .3 .7 .5 .5];
o=0;
for i=1:5
o=o-((x-aSH(i,:))*(x-aSH(i,:))'+cSH(i))^(-1);
end
end
% F22
function o = F22(x)
aSH=[4 4 4 4;1 1 1 1;8 8 8 8;6 6 6 6;3 7 3 7;2 9 2 9;5 5 3 3;8 1 8 1;6 2 6 2;7 3.6 7 3.6];
cSH=[.1 .2 .2 .4 .4 .6 .3 .7 .5 .5];
o=0;
for i=1:7
o=o-((x-aSH(i,:))*(x-aSH(i,:))'+cSH(i))^(-1);
end
end
% F23
function o = F23(x)
aSH=[4 4 4 4;1 1 1 1;8 8 8 8;6 6 6 6;3 7 3 7;2 9 2 9;5 5 3 3;8 1 8 1;6 2 6 2;7 3.6 7 3.6];
cSH=[.1 .2 .2 .4 .4 .6 .3 .7 .5 .5];
o=0;
for i=1:10
o=o-((x-aSH(i,:))*(x-aSH(i,:))'+cSH(i))^(-1);
end
end
function o=Ufun(x,a,k,m)
o=k.*((x-a).^m).*(x>a)+k.*((-x-a).^m).*(x<(-a));
end
%=============初始化=====================
function X=initialization(SearchAgents_no,dim,ub,lb)
Boundary_no= size(ub,2); % 边界数
%如果所有变量的边界相等,用户对ub和lb都输入一个标志号
if Boundary_no==1
X=rand(SearchAgents_no,dim).*(ub-lb)+lb;
end
%===如果每个变量具有不同的lb和ub==
if Boundary_no>1
for i=1:dim
ub_i=ub(i);
lb_i=lb(i);
X(:,i)=rand(SearchAgents_no,1).*(ub_i-lb_i)+lb_i;
end
end
%====蚂蚁随机游走=============
function [RWs]=Random_walk_around_antlion(Dim,max_iter,lb, ub,antlion,current_iter)
if size(lb,1) ==1 && size(lb,2)==1 %检查变量是否越限
lb=ones(1,Dim)*lb;
ub=ones(1,Dim)*ub;
end
if size(lb,1) > size(lb,2)
lb=lb';
ub=ub';
end
I=1;
if current_iter>max_iter/10
I=1+100*(current_iter/max_iter);
end
if current_iter>max_iter/2
I=1+1000*(current_iter/max_iter);
end
if current_iter>max_iter*(3/4)
I=1+10000*(current_iter/max_iter);
end
if current_iter>max_iter*(0.9)
I=1+100000*(current_iter/max_iter);
end
if current_iter>max_iter*(0.95)
I=1+1000000*(current_iter/max_iter);
end
%===缩小边界向蚁群收敛==========
lb=lb/(I);
ub=ub/(I);
% 围绕蚁狮移动[lb ub]的区间[lb+anlion ,ub+antlion]
if rand<0.5
lb=lb+antlion;
else
lb=-lb+antlion;
end
if rand>=0.5
ub=ub+antlion;
else
ub=-ub+antlion;
end
%该函数创建n个随机游走,并对lb和ub向量进行归一化处理
for i=1:Dim
X = [0 cumsum(2*(rand(max_iter,1)>0.5)-1)'];
%[a b]--->[c d]
a=min(X);
b=max(X);
c=lb(i);
d=ub(i);
X_norm=((X-a).*(d-c))./(b-a)+c;
RWs(:,i)=X_norm;
end
%====轮盘赌随机选择==============
function choice = RouletteWheelSelection(weights)
accumulation = cumsum(weights);
p = rand() * accumulation(end);
chosen_index = -1;
for index = 1 : length(accumulation)
if (accumulation(index) > p)
chosen_index = index;
break;
end
end
choice = chosen_index;3.2 运行结果
F9:


F12:


F23: