归约
可将自底向上语法分析过程看成将一个串ω"归约"为文法开始符号的过程.
在每个归约步骤中,
一个与某产生式体相匹配的特定子串被替换为该产生式头部的非终结符号.
句柄剪枝
如有S=>^{*}_{rm} αAω =>_{rm} αβω,
则A->β是αβω的一个句柄.
最右句型γ的一个句柄是满足下叙条件的产生式A->β及β在γ出现的位置:
将此位置的β替换为A后得到的串是γ的某个最右推导序列位于γ之前的最右句型.
ω只含终结符号.
从被分析的终结符号串ω开始,
如ω是当前文法的句子,令ω=γ_{n},是某个最右推导的第n个最右句型.
在γ_{n}寻找β_{n},将其替换为对应产生式头部.
得到前一最右句型.直到得到S.
移入-归约语法分析
句柄总是在栈的顶端.
考虑任意最右推导两个连续步骤所有可能
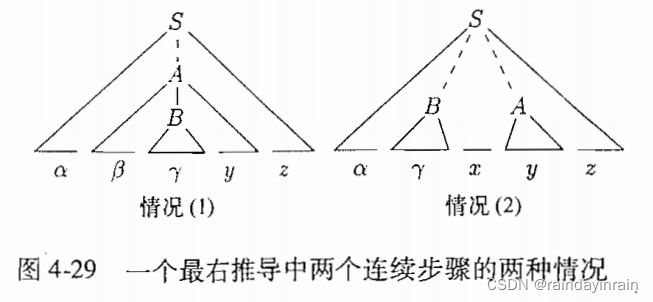
反向考虑1,
一个移入-归约语法分析器刚刚到达
栈 输入
$αβγ yz$
将γ归约为B
$αβB yz$
多次移入
$αβBy z$
βBy归约为A
$αA z$
反向考虑2,类似.
两种情况下句柄都在栈顶.[k之前按假设句柄都在栈顶.考察k步,[移入/归约]证明k步处理后,句柄仍在栈顶.]
项和LR(0)自动机
一个LR语法分析器通过维护一些状态,
用这些状态表明我们在语法分析过程中所处的位置,
进而做出移入-归约决定.
这些状态代表了"项"集合.
一个文法G的一个LR(0)项是G的一个产生式再加上一个位于它的体中某处的点.
故,产生式A->XYZ产生了四个项.
A->.XYZ
A->X.YZ
A->XY.Z
A->XYZ.
产生式A->ε只有一个A->.
一个称为规范LR(0)项集族的一组项集提供了构建一个确定有穷自动机的基础.
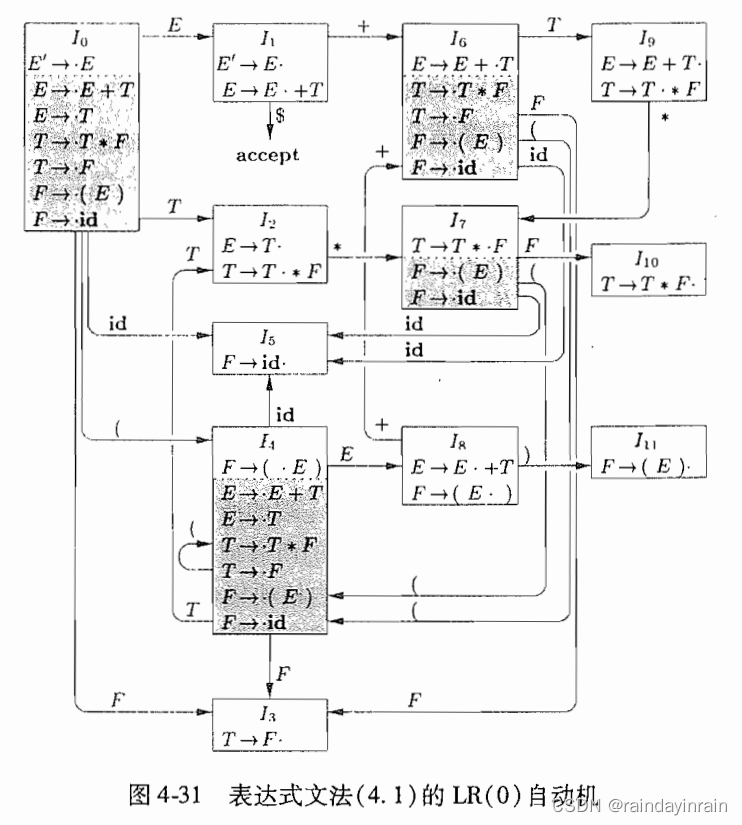
这个LR(0)自动机的每个状态代表了规范LR(0)项集族中的一个项集.
表达式文法4-1对应的自动机显示在图4-31.
为构造一个文法的规范LR(0)项集族,
定义一个增广文法,两个函数CLOSURE和GOTO.
如G是一个以S为开始符号的文法,
则G的增广文法G'是在G中加上新开始符号S'和产生式S'->S得到的.
项集的闭包
如I是文法G的一个项集,
则CLOSURE(I)是根据下面两个规则从I构造得到的项集
1.一开始,将I中的各个项加入到CLOSURE(I)中.
2.对CLOSURE(I)中的A->α.Bβ.
B->γ是B的一个产生式,
项B->.γ加入CLOSURE(I).
SetOfItems CLOSURE(I)
{
J = I
repeat
for(J中的每个项A->α.Bβ)
for(G的每个产生式B->γ)
将B->.γ加入J中[自动过滤重复]
until 在某轮没新的项被加入J中
return J
}
项的分类:
1.S'->.S及点不在最左端的所有项
2.除S'->.S外,点在最左端的所有项
GOTO函数
GOTO(I, X)被定义为I中所有形如[A->α.Xβ]的项所对应的项[A->αX.β]的集合的闭包.
GOTO(I,X)存在下,表示I下遇到X执行移入.
GOTO(I,X)存在情况下,
I中不能同时存在可对X进行归约的产生式,因为这样会产生冲突
void items(G')
{
C = {
CLOSURE({
[S'->.S]})}
repeat
for(C中的每个项集I)
for(每个文法符号X)
如果GOTO(I,X)存在,加入C[防止项集重复]
}
LR语法分析表的结构
语法分析表由两个部分组成:ACTION和GOTO
1.ACTION函数有两个参数,一个是状态i,另一个是终结符号a[或输入结束标记$]
ACTION[i, a]的取值可有下列四种形式:
a. 移入j,把输入符号a移入栈,用状态j代表a
b.归约A->β,把栈顶的β归约为产生式头,状态对应调整
c.接受
d.报错
LR语法分析器的格局
语法分析器的完整状态包括:它的栈和余下的输入
LR语法分析器的格局是一个形如(s_{0}...s_{m},a_{i}...a_{n}$)的对.
第一个分量是栈中内容,第二个分量是余下输入.
上述格局表示了如下的最右句型:
X_{1}...X_{m}a_{i}...a_{n}
每个X_{i}和s_{i}存在一一对应关系.
s_{i-1}通过X_{i}到达s_{i}.
LR语法分析器的行为
语法分析器根据上面的格局决定下一个动作时,
先读入当前输入符号a_{i}和栈顶状态s_{m}.
再在分析动作表中查询ACTION[s_{m}, a_{i}].
1.如ACTION[s_{m}, a_{i}] = 移入s,
则语法分析器执行一次移入动作;
将下一状态s移入栈中,进入
(s_{0}...s_{m}s, a_{i+1}...a_{n}$)
2.如ACTION[s_{m}, a_{i}] = 规约A->β,
则语法分析器执行一次归约动作,进入
(s_{0}...s_{m-r}s, a_{i}...a_{n}$)
其中,r是β的长度,且s=GOTO[s_{m-r}, A]
3.如ACTION[s_{m}, a_{i}] = 接受,完成语法分析
4.如ACTION[s_{m}, a_{i}] = 报错.
LR语法分析算法
输入:一个输入串ω和一个LR语法分析表
这个表描述了文法G的ACTION和GOTO
输出:
如ω在L(G)中,输出ω的自底向上语法分析过程中的归约步骤;
否则,给出错误指示.
方法:
最初,语法分析器栈中内容为初始状态s_{0},
输入缓冲区中内容为ω$.
语法分析器执行下述程序
令a为ω$的第一个符号;
while(1)
{
令s是栈顶的状态;
if(ACTION[s, a] = 移入t)
{
将t压入栈中;
令a为下一个输入符号;
}
else if(ACTION[s, a] = 归约A->β)
{
从栈中弹出|β|个符号;
令t为当前的栈顶状态;
将GOTO[t, A]压入栈中;
输出产生式A->β;
}
else if(ACTIOIN[s, a] = 接受)
{
break;
}
else
{
调错误恢复例程;
}
}
构造SLR语法分析表
构造一个SLR语法分析表
输入:一个增广文法G'
输出:G'的SLR语法分析表函数ACTION和GOTO
方法:
1.方法决定
a.如 [A->α.aβ] 在I_{i}中
且GOTO(I_{i}, a) = I_{j},
则将ACTION[i, a]设置为"移入j".
b.如 [A->α.] 在I_{i}中,
则对FOLLOW(A)中所有a,
将ACTION[i, a]设置为"归约A->α"
这里A != S'
c.如 [S'->S.] 在I_{i}中,
则将ACTION[i, $]设置为"接受"
3.状态i对于各个非终结符号A的GOTO转换使用下面的规则构造得到:
如GOTO(I_{i}, A) = I_{j},
则GOTO[i, A] = j.
4.对2,3,没定义的条目,设为报错.
5.语法分析器的初始状态就是根据[S' -> .S]所在项集得到的.
如果文法,按上述处理,在某步产生归约/移入冲突,
则该文法的语法分析无法按上述方式处理.
可行前缀
E =>^{*}_{rm} F * id =>_{rm} (E) * id
在语法分析的不同时刻,
栈中存放的内容可以是( (E (E),但不会是(E) *
因为*移入前,(E)会被归约为F.
可以出现在一个移入-归约语法分析器栈中的最右句型前缀称为可行前缀
一个可行前缀是一个最右句型的前缀,
且它没越过该最右句型的最右句柄的右端.
据此定义,
总是可在一个可行前缀后增加一些终结符号来得到一个最右句型.
如存在一个推导过程
S=>^{*}_{rm} αAω =>_{rm} αβ_{1}β_{2}ω
就说项A -> β_{1}.β_{2} 对可行前缀αβ_{1}有效
可行前缀是可以出现在语法分析栈中的一个句型.
对可行前缀有效的项,意味着可行前缀后再添加0个或多个文法符号后,将按此项进行归约.
对文法计算出所有可行前缀,
对每个可行前缀计算出所有对其有效的项.
实际上,
LR语法分析理论的核心定理是:
如我们在某个文法的LR(0)自动机中从初始状态开始
沿着标号为某个 可行前缀γ 的路径到达一个状态,
则该状态对应的项集就是 γ 的 有效项的集合.

