动态规划法求解问题的时候,空间换时间的时候,怎么去记,应该记什么。空间计算值得过程可以有效的理解备忘录,备忘录实际上就是一张表格,帮助我们求解子问题。
文章目录
一、操作过程:
现在有五个矩阵,有六个数来表示,每个矩阵的行号、列号都是已知的,就是从里面挑出相邻的两个值,六个数表示五个矩阵的项矩阵链,接下来记录子问题。
1、输入
P = < 30, 35, 15, 5, 10, 20 >, n = 5
2、矩阵链
A1A2A3A4A5,其中A1:30×35,A2:35×15,A3:15×5,A4:5×10,A5:10×20
3、备忘录
存储所有子问题的最小乘法次数及得到这个值的划分位置.
(1)r表示长度
首先是长度为1的,把r=1这一行先写好,这一行刚好有5列,每一列的值都是0。这个m表示最少的次数。
r=2长度为2这一行的计算要借助第一行来计算
(2)例:
例如m[2,5]的计算,k的位置可以有很多种选择,第1种选择,左边界2和2所构成的子链,右边是3→5所构成的另一个子链,m[2,2]和m[3,5]的结果,因为是逐层计算的,所以已知m[2,2]和m[3,5]的结果进行计算。
m[2,5] = min{ 0 +2800+35x15x20,2625+1000+35x5x20,4735+0+35x10x200 }=7125
把左边的结果加上右边的结果,第2个矩阵的规模是35x15,第3到第5构成的子链规模是15x20,所以最后乘到最后,一定是以第5个矩阵结束的列号作为最终的列号。综合求解过程:子问题1、子问题2、综合的过程。计算出来


(3) 过程
①r=1
m[1][1]= m[2][2] = m[3][3] = m[4][4] =m[5][5]=0
②r=2
m[1][2] = 30x35x15 = 15750
m[2][3] = 35x15x5 = 2625
m[3][4] = 15x5x10 = 750
m[4][5] = 5x10x20 = 1000
③r=3
m[1][3] =min(m[1][1]+m[2][3]+A1(A2A3),m[1,2]+m[3,3]+ (A1A2)A3
=min(m[1][1]+m[2][3]+P0P1P3,m[1,2]+m[3,3]+P0P2P3
=min(0+2625+30x35x5,15750+0+30x15x5)
=min(7875,18000)=36,s[1][3]=1
m[2][4]=min(m[2][2]+m[3][4]+A2(A3A4),m[2][3]+m[4][4]+(A2A3)A4
=4375,s[2][4]=3
m[3][5]==min(m[3][3]+m[4][5]+A3(A4A5),m[3][4]+m[5][5]+(A3A4)A5
=2500,s[3][5]=3
④r=4
m[1][4]=min(m[1][1]+m[2][4]+ A1(A2A3A4)+m[1][2]+m[3][4] + (A1A2)(A3A4), m[1][3]+m[4][4]+ (A1A2A3)A4
=9375,s[1][4]=3
m[2][5]=min(m[2][2]+m[3][5]+ A2(A3A4A5),m[2][3]+m[4][5] + (A2A3)(A4A5), m[2][4]+m[5][5]+ (A2A3A4)A5
=7125,s[2][5]=3
⑤r=5
m[1][5]=min(m[1][1]+m[2][5]+ A1(A2A3A4A5),m[1][2]+m[3][5] + (A1A2)(A3A4A5) ,m[1][3]+m[4][5]+(A1A2A3)(A4A5)
=11875,s[1][5]=3
备忘录
| r=1 | m[1][1]=0 | m[2][2]=0 | m[3][3]=0 | m[4][4]=0 | m[5][5]=0 |
|---|---|---|---|---|---|
| r=2 | m[1][2]=15750 | m[2][3]=2625 | m[3][4]=750 | m[4][5]=1000 | |
| r=3 | m[1][3]=7875 | m[2][4]=4375 | m[3][5]=2500 | ||
| r=4 | m[1][4]=9375 | m[2][5]=7125 | |||
| r=5 | m[1][5]=11875 |
(4)标记函数s[i,j]
| r=2 | s[1][2]=1 | m[2][3]=2 | m[3][4]=3 | m[4][5]=4 | |
|---|---|---|---|---|---|
| r=3 | m[1][3]=1 | m[2][4]=3 | m[3][5]=3 | ||
| r=4 | m[1][4]=3 | m[2][5]=3 | |||
| r=5 | m[1][5]=3 |
解的追踪:s[1,5]=3⇒(A1A2A3)(A4A5)
s[1,3]=1⇒A1(A2A3)
输出
计算顺序: (A1(A2A3))(A4A5)
最少的乘法次数:m[1,5]=11875
二、递推方程
其实比较难想到的,比较难进行的就是递推方程,要想到问题如何分解,为什么会有这样的关系,这些是难于想到的,尤其是在一个问题在做一个新的问题的时候,可能不是那么明显能看出来。
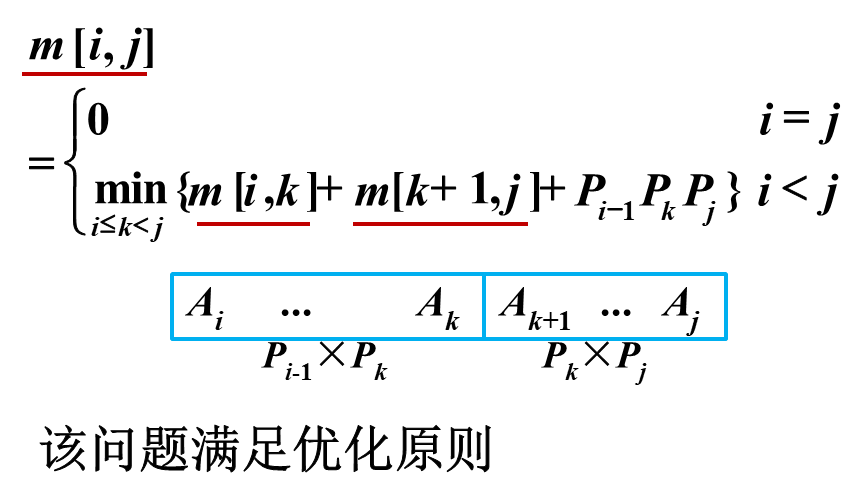
m[i,j] :得到 Ai…j 的最少的相乘次数
三、动态规划算法
1、子问题划分
Ai…j :矩阵链 Ai Ai+1 … Aj,边界i, j
输入向量: < Pi-1, Pi, … , Pj >
其最好划分的运算次数: m[i, j]
2、子问题的依赖关系
最优划分最后一次相乘发生在矩阵k 的位置,即
Ai…j = A~i …k~ Ak+1…j
Ai…j 最优运算次数依赖于 Ai…k 与 Ak+1…j 的最优运算次数