数据结构（六）：二叉树的创建、递归遍历与非递归遍历、层次遍历

目录

一、二叉树的存储结构

二、创建一棵二叉树

三、二叉树的递归遍历

【先序遍历】

【中序遍历】

【后序遍历】

四、二叉树的非递归遍历

【中序遍历】

【先序遍历】

【后序遍历】

 五、二叉树的层次遍历

---

一、二叉树的存储结构

二叉树可采用顺序存储与链式存储，顺序存储的空间利用率较低，故一般采用链式存储。

链式存储结构描述如下：

typedef struct BiTNode
{
	ElemType data;  //数据域
	struct BiTNode *lchild, *rchild;  //左右孩子指针
} BiTNode, *BiTree;

二、创建一棵二叉树

例如：输入二叉树的先序序列，即可得到一颗二叉树

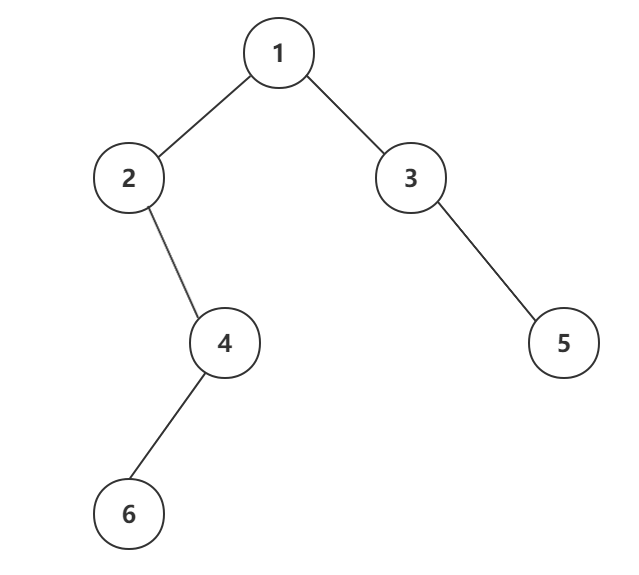
例如：我们输入这颗二叉树的先序序列（空节点用0表示）：1 2 0 4 6 0 0 0 3 0 5 0 0

然后我们输出任意几个结点的data数值，验证二叉树是否正确。

#include<iostream>
using namespace std;
#define ElemType int

typedef struct BiTNode
{
	ElemType data;
	struct BiTNode *lchild, *rchild;
} BiTNode, *BiTree;

void createBiTree(BiTree& T)
{
	ElemType d;
	cin >> d;
	if (d == 0)
		T = NULL;
	else
	{
		T = (BiTree)malloc(sizeof(BiTNode));
		T->data = d;
		createBiTree(T->lchild);
		createBiTree(T->rchild);
	}
}

int main()
{
	BiTree root = NULL; //定义一棵空树
	cout << "请按先序序列输入各个结点（空节点用0表示）：" << endl;
	createBiTree(root);
	//输出测试
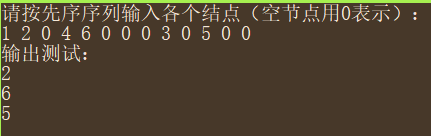
	cout << "输出测试：" << endl;
	cout << root->lchild->data << endl;
	cout << root->lchild->rchild->lchild->data << endl;
	cout << root->rchild->rchild->data << endl;
}

三、二叉树的递归遍历

【先序遍历】

void PerOrder(BiTree T)
{
	if(T!=NULL)
	{
		cout << T->data << " "; //visit(root);
		PerOrder(T->lchild);
		PerOrder(T->rchild);
	}
}

【中序遍历】

void InOrder(BiTree T)
{
	if(T!=NULL)
	{
		InOrder(T->lchild);
		cout << T->data << " "; //visit(root);
		InOrder(T->rchild);
	}
}

【后序遍历】

void PostOrder(BiTree T)
{
	if(T!=NULL)
	{
		PostOrder(T->lchild);
		PostOrder(T->rchild);
		cout << T->data << " "; //visit(root);
	}
}

仍以前面的二叉树为例，输入结点创建二叉树后，对其进行先序、中序、后序遍历输出：

#include<iostream>
using namespace std;
#define ElemType int

typedef struct BiTNode
{
	ElemType data;
	struct BiTNode *lchild, *rchild;
} BiTNode, *BiTree;

void createBiTree(BiTree& T)
{
	ElemType d;
	cin >> d;
	if (d == 0)
		T = NULL;
	else
	{
		T = (BiTree)malloc(sizeof(BiTNode));
		T->data = d;
		createBiTree(T->lchild);
		createBiTree(T->rchild);
	}
}

void PerOrder(BiTree T)
{
	if(T!=NULL)
	{
		cout << T->data << " "; //visit(root);
		PerOrder(T->lchild);
		PerOrder(T->rchild);
	}
}

void InOrder(BiTree T)
{
	if(T!=NULL)
	{
		InOrder(T->lchild);
		cout << T->data << " "; //visit(root);
		InOrder(T->rchild);
	}
}

void PostOrder(BiTree T)
{
	if(T!=NULL)
	{
		PostOrder(T->lchild);
		PostOrder(T->rchild);
		cout << T->data << " "; //visit(root);
	}
}

int main()
{
	BiTree root = NULL; //定义一棵空树
	cout << "请按先序序列输入各个结点（空节点用0表示）：" << endl;
	createBiTree(root);

	//递归遍历
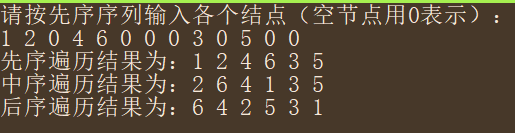
	cout << "先序遍历结果为：";
	PerOrder(root);
	cout << endl;
	cout << "中序遍历结果为：";
	InOrder(root);
	cout << endl;
	cout << "后序遍历结果为：";
	PostOrder(root);
	cout << endl;
}

注意：递归遍历的特点是：

①每个节点都访问一次且仅访问一次；

②递归遍历中，递归工作栈的深度恰好为树的深度

四、二叉树的非递归遍历

【中序遍历】

以此棵二叉树为例：

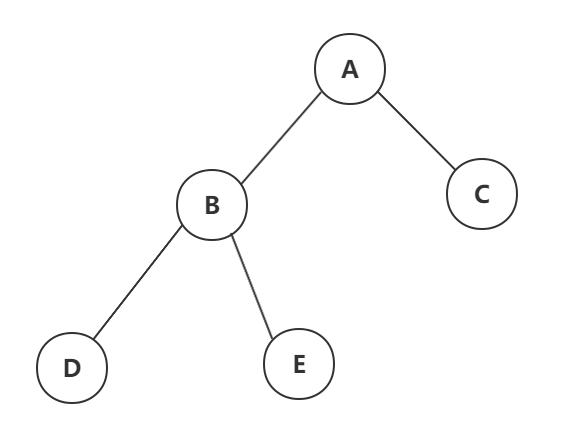
我们借助栈来分析中序遍历（非递归）的访问过程： 沿着根的左孩子，依次入栈，直到左孩子为空。 说明已经找到可以输出的结点，此时栈内元素依次为 A,B,D 栈顶元素出栈并访问：若其右孩子为空，继续执行 （步骤2） ，若其右孩子不空，将右子树转执行 （步骤1）. 栈顶D出栈并访问，它是中序序列的第一个结点；D右孩子为空，栈顶B出栈并访问；B右孩子不空，将其右孩子E入栈，E左孩子为空，栈顶E出栈并访问；E右孩子为空，栈顶A出栈并访问；A右孩子不空，将其右孩子C入栈，C左孩子为空，栈顶C出栈并访问。 所以，中序序列为：D B E A C

【先序遍历】

        先序遍历与中序遍历基本思想类似，只需把访问结点操作放在入栈操作前面即可，具体参考下面的代码。

【后序遍历】

        后续遍历的非递归实现是三种遍历中最难的，具体思路为：

沿着根的左孩子，依次入栈，直到左孩子为空。 此时栈内元素为A B D 读栈顶元素：若其右孩子不空且未被访问过，将右子树执行 （步骤1）；否则，栈顶元素出栈并访问。 栈顶D的右孩子为空，出栈并访问，他是后序序列的第一个结点；栈顶B的右孩子不空且未被访问过，E入栈，栈顶E的左右孩子均为空，出栈并访问；栈顶B的右孩子不空但已被访问，B出栈并访问；栈顶A的右孩子不空且未被访问过，C入栈，栈顶C的左右孩子均为空，出栈并访问；栈顶A的右孩子不空但已被访问，A出栈并访问。 由此，后序序列为：D E B C A

代码

#include<iostream>
#include <stack>
using namespace std;
#define ElemType int

typedef struct BiTNode
{
	ElemType data;
	struct BiTNode *lchild, *rchild;
} BiTNode, *BiTree;

void createBiTree(BiTree& T)
{
	ElemType d;
	cin >> d;
	if (d == 0)
		T = NULL;
	else
	{
		T = (BiTree)malloc(sizeof(BiTNode));
		T->data = d;
		createBiTree(T->lchild);
		createBiTree(T->rchild);
	}
}

//先序遍历
void PerOrder2(BiTree T)
{
	stack<BiTree> S;
	BiTree p = T;
	while (p || !S.empty())
	{
		if (p)
		{
			cout << p->data << " ";  //visit(p);
			S.push(p);
			p = p->lchild;
		}
		else
		{
			p = S.top();
			S.pop();
			p = p->rchild;
		}
	}
}

//中序遍历
void InOrder2(BiTree T)
{
	stack<BiTree> S; // #include<stack>
	BiTree p = T; //p是遍历指针
	while (p || !S.empty())
	{
		if (p)
		{
			S.push(p);
			p = p->lchild;
		}
		else
		{
			p = S.top();
			S.pop(); //栈顶元素出栈
			cout << p->data << " ";  //visit(p);
			p = p->rchild; //转向出栈结点的右子树
		}
	}
}

//后序遍历
void PostOrder2(BiTree T)
{
	stack<BiTree> S;
	BiTree p = T, r = NULL; //r是辅助指针，指向最近访问过的结点
	while (p || !S.empty())
	{
		if (p)
		{
			S.push(p);
			p = p->lchild;
		}
		else
		{
			p = S.top();
			if (p->rchild && p->rchild != r) //若右子树存在，且未被访问过
				p = p->rchild;
			else
			{
				S.pop();
				cout << p->data << " ";  //visit(p);
				r = p;  //记录最近访问过的结点
				p = NULL;  //结点访问完后，重置p指针
			}
		}
	}
}

int main()
{
	BiTree root = NULL; //定义一棵空树
	cout << "请按先序序列输入各个结点（空节点用0表示）：" << endl;
	createBiTree(root);

	//非递归遍历
	cout << "先序遍历（非递归）结果为：";
	PerOrder2(root);
	cout << endl;
	cout << "中序遍历（非递归）结果为：";
	InOrder2(root);
	cout << endl;
	cout << "后序遍历（非递归）结果为：";
	PostOrder2(root);
	cout << endl;
}

 五、二叉树的层次遍历

        要进行层次遍历，需要借助一个队列。先将二叉树根结点入队，然后出队，访问出队结点，若它有左子树，则将左子树根结点入队；若它有右子树，则将右子树根结点入队。然后出队，访问出队结点……如此反复，直至队列为空。

void LevelOrder(BiTree T)
{
	queue<BiTree> Q; //#include<queue>
	BiTree p;
	Q.push(T); //将根节点入队
	while (!Q.empty()) //队列不空则循环
	{
		p = Q.front();
		Q.pop(); //队头结点出队
		cout << p->data << " "; //visit(p);
		if (p->lchild != NULL)
			Q.push(p->lchild);
		if (p->rchild != NULL)
			Q.push(p->rchild);
	}
}