深入理解Matrix和认识齐次坐标系

概述

Android中的Matrix是一个3x3的矩阵，在定义View中存在广泛应用，包括动画、改变图片大小，增加图像滤镜等等，这里我们来探讨一下安卓中Matrix的实现原理和一些有趣的应用。

原理

1. 理解矩阵，首先稍微复习下矩阵的原理和计算方式

数学上，矩阵是由一个 m x n 的阵列构成，最普遍的用法是用来表达线性方程式

$$\left[\begin{matrix} a & b \\ c & d \end{matrix}\right] * \left[\begin{matrix} x \\ y \end{matrix}\right] = \left[\begin{matrix} c1\\ c2 \end{matrix}\right] ----等价于---> \begin{cases} ax + by = c1\\ cx + dy = c2 \end{cases}$$

矩阵乘法示例：

$$\begin{bmatrix} 1 & 0 & 2 \\ -1 & 3 & 1 \\ \end{bmatrix} \times \begin{bmatrix} 3 & 1 \\ 2 & 1 \\ 1 & 0 \end{bmatrix} = \begin{bmatrix} (1 \times 3 + 0 \times 2 + 2 \times 1) & (1 \times 1 + 0 \times 1 + 2 \times 0) \\ (-1 \times 3 + 3 \times 2 + 1 \times 1) & (-1 \times 1 + 3 \times 1 + 1 \times 0) \\ \end{bmatrix} = \begin{bmatrix} 5 & 1 \\ 4 & 2 \\ \end{bmatrix}$$

矩阵的乘法满足结合律和对矩阵加法的分配律（左分配律和右分配律）：

$$结合律：（AB)C = A(BC) \\ 左分配率：（A + B) C = AC + BC\\ 右分配率： C(A + B) = CA + CB\\$$

矩阵不满足交换律：

$$A B\neq BA$$

2. Matrix结构

   Matrix是一个3x3的矩阵，以下是这9个参数每个参数代表的意义：

$$\left[\begin{matrix} MSCALE\_X& MSKEW\_X & MTRANS\_X\\ MSKEW\_Y& MSCALE\_Y & MTRANS\_Y \\ MPERSP\_0 & MPERSP\_1 & MPERSP\_2 \end{matrix}\right]$$

由于矩阵可以表达线性方程式，所以对某一坐标点乘以矩阵可以如下表示(左侧为基础矩阵，忽略w，稍后会讲到)

$$\left[\begin{matrix} 1& 0 & 0\\ 0& 1 & 0 \\ 0 & 0 & 1 \end{matrix}\right] * \left[\begin{matrix} x\\ y \\ w \end{matrix}\right] = \left[\begin{matrix} x\\ y \\ w \end{matrix}\right]$$

那么我们对矩阵每个参数都加上相应运算，则如下：

$$\left[\begin{matrix} a& b & c\\ d& e & f \\ g & h & i \end{matrix}\right] * \left[\begin{matrix} x\\ y \\ w \end{matrix}\right] = \left[\begin{matrix} ax + by +cw\\ dx + ey + fw \\ gx + hy + iw \end{matrix}\right]$$

① 缩放(scale)：

$$\left[\begin{matrix} a& 0 & 0\\ 0& b & 0 \\ 0 & 0 & 1 \end{matrix}\right] * \left[\begin{matrix} x\\ y \\ w \end{matrix}\right] = \left[\begin{matrix} ax \\ by \\ w \end{matrix}\right]$$

​ *当a或者b为负数的时候，会产生翻转（镜像）效果

② 错切(skew)

$$\left[\begin{matrix} 1 & a & 0\\ b& 1 & 0 \\ 0 & 0 & 1 \end{matrix}\right] * \left[\begin{matrix} x\\ y \\ w \end{matrix}\right] = \left[\begin{matrix} x + ay \\ bx + y \\ w \end{matrix}\right]$$

③ 旋转(rotate)

$$\left[\begin{matrix} cos(\theta) & -sin(\theta) & 0\\ sin(\theta) & cos(\theta) & 0 \\ 0 & 0 & 1 \end{matrix}\right] * \left[\begin{matrix} x\\ y \\ w \end{matrix}\right] = \left[\begin{matrix} cos(\theta)x - sin(\theta)y \\ sin(\theta)x + cos(\theta)y \\ w \end{matrix}\right]$$

这里的逻辑较为抽象一点，但可以使用公式推导：

设在三维坐标系Oxyz中，有一点P(x,y,z)绕Z轴旋转α度后得新坐标P'(x', y', z' )，因绕Z旋转，忽略Z轴转换为极坐标系Or，如下图所示

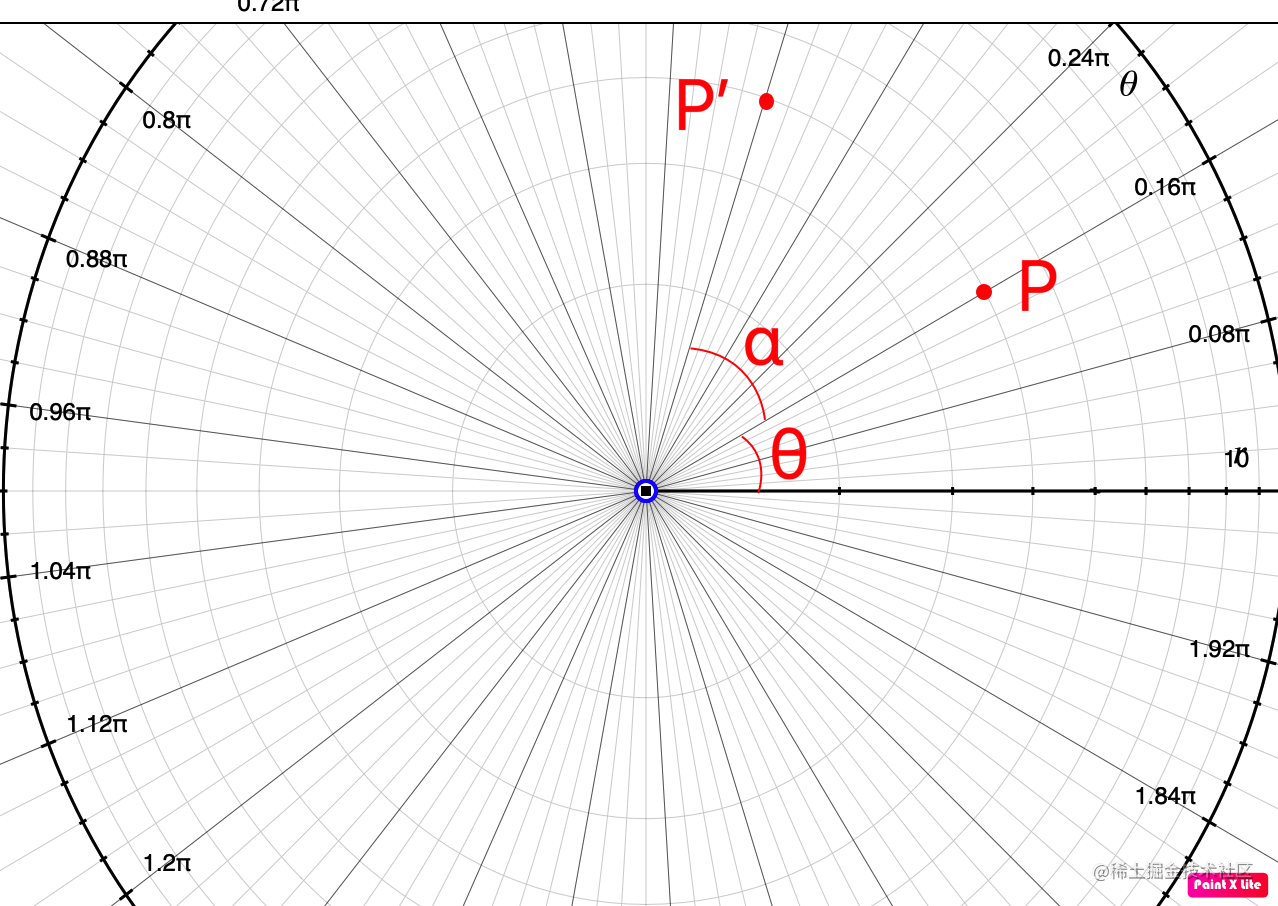
设P点与X轴夹角为θ，可得方程

$$P点方程 \begin{cases} x = r · cos\theta\\ y = r · sin\theta \end{cases}$$

以及

$$P'点方程 \begin{cases} x' = r · cos(\theta+\alpha)\\ y’ = r · sin(\theta + \alpha) \end{cases}$$

由以上两方程可得：

$$\begin{cases} x' = x · cos\alpha - y · sin\alpha\\ y’ = y · cos\alpha + x · sin\alpha \end{cases}$$

④ 位移(translate)

$$\left[\begin{matrix} 1& 0 & m\\ 0& 1 & n \\ 0 & 0 & 1 \end{matrix}\right] * \left[\begin{matrix} x\\ y \\ w \end{matrix}\right] = \left[\begin{matrix} x + m \\ y + n \\ w \end{matrix}\right]$$

齐次坐标系

​ 我们注意到，上面描述坐标点用的是*(x, y, w)*，这里的w指的并不是Z轴，而是计算机中为了方便计算投影人为添加的一个维度，这种坐标系叫做齐次坐标系（homogenous coordinates)

​ 在欧式几何空间中，两条平行的直线是不能相交的，然而，在投影空间中，是可以相交的。比如下图的铁路，在无穷远的地方交为一点。

欧几里得空间或者笛卡尔空间可以方便的描述2D/3D几何，但是不足以处理投影空间（欧几里得几何是射影几何的子集）。

在笛卡尔坐标系中，一个二维点可以表示为( x , y )，但是如果这个点事无穷远，该怎么表示呢？无穷远的点应该表示为( ∞ , ∞ ) ，计算机中这样的表示毫无意义。

August Ferdinand Möbius 引入的齐次坐标系使得在投影空间中计算图形和几何成为可能。齐次坐标是一种用 N+1 个数表示 N 维坐标的方法， 要制作 2维齐次坐标，我们只需在现有坐标中添加一个附加变量w 。

因此，笛卡尔坐标中的一个点(X, Y )在齐次坐标中变为(x, y, w) 。并且笛卡尔坐标系中的X和Y用同构中的x、y和w重新表示为；

$$X = x/w\\ Y = y/w$$

例如，笛卡尔 (1, 2) 中的一个点在 Homogeneous 中变为 (1, 2, 1)。如果一个点 (1, 2) 向无穷大移动，则它在笛卡尔坐标中变为 (∞,∞)。由于 (1/0, 2/0) ≈ (∞,∞)，它在齐次坐标中变为 (1, 2, 0)。请注意，我们可以在不使用“∞”的情况下表示无穷远点了。

齐次坐标是计算机图形学的重要手段之一，它既能够明确区分向量和点，同时也更易用于进行仿射（线性）几何变换。

​ 从上面的描述我们知道齐次坐标是用于投影几何里的坐标系统，和平时我们用的笛卡尔坐标系一样，是帮助我们理解的工具。但因为这是两种不同的坐标系，我们需要跳出笛卡尔坐标系，以更宏观的思维来理解，不然有些场景会让我们困惑。

　　首先我们把上面的这个投影描述图印在脑海中。

　　考虑一个点p，它的笛卡尔坐标是(x,y)，齐次坐标是(x,y,1)，齐次坐标比笛卡尔坐标多一个维度，按照现在书上和网络上的理解基本都是说笛卡尔坐标系就是齐次坐标系中w=1的那个平面，(x,y,1)是齐次坐标(kx,ky,k)表示的点在w=1上的映射。

​ 由此可以理解，当一个图形的x和y保持不变，w增大时，我们会看到这个图形会离我们远去，在屏幕上的表现就是变小，这样我们就可以理解Android Matrix中MPERSP_0、MPERSP_1、MPERSP_2这三个参数的意义。

​ MPERSP_2就代表w本身，在默认矩形中等于1，增大图像便会相应变小，减小则图像就会增大，MPERSP_1增大，图像便会跟随y值的增大而变小，同样MPERSP_0增大便会随x值增大而变小，如下图所示：

​ 这三个值没有封装相应API，所以不推荐修改，如果需要修改，只能通过setValues方法。

Matrix 相关API

上面已经讲了矩阵的乘法，包括缩放、错切、旋转和位移是如何实现的，本质上都是依靠矩阵的乘法。但是因为矩阵的乘法不满足交换律，所以执行的顺序也至关重要。上述四种基本操作Matrix已经进行了完整的封装，每一种操作都有三种实现方式：前乘（pre），后乘（post）和设置（set）。

对于单位矩阵M，乘以矩阵T，三种实现方式有以下区别

前乘（pre）：

$$M' = M×T$$

后乘（post）：

$$M' = T×M$$

设置（set）：

​ 这里使用的不是乘法，而是将原来的矩阵重置，更换为新的矩阵，所以此类操作会导致之前的操作失效。

假如我们有三个矩阵M、T、R，分别使用前乘，那么公式如下

$$S=M×T×R$$

如果分别使用后乘，则

$$S= R×T×M$$

如果M和T先进行前乘，然后与R进行后乘，则

$$S=R×(M×T)$$

前乘和后乘混合使用时容易引起混乱，所以建议非必要情况下，只使用同一种运算方式。

其他方法：

API	方法
setValues	给矩阵设置一个长度为9的数组，此方法可以自由设置矩阵每个位置的值
invert	求逆矩阵
mapPoints	给特定点执行矩阵操作
mapRect	给特定矩形执行矩阵操作
mapVectors	给特定向量执行矩阵操作
preConcat/postConcat	前乘/后乘特定矩阵
set/pre/postScale	缩放操作
set/pre/postSkew	错切操作
set/pre/postRotate	旋转操作
set/pre/postTranslate	位移操作
setPolyToPoly	设置矩阵，使指定的src点映射到指定的dst点。
setRectToRect	设置矩阵，将指定矩形映射到目标矩形