针孔模型 + 透镜

无法记录物体的信息,因为胶片上的点(右侧),记录了A和B两个地方的信息,那么生成的图像就是模模糊糊的一团
如何解决这个问题?(利用针孔摄像机)
我们在中间添加隔板(隔板中间有针孔),使物体和胶片呈现一对一的关系

摄像机箱体:
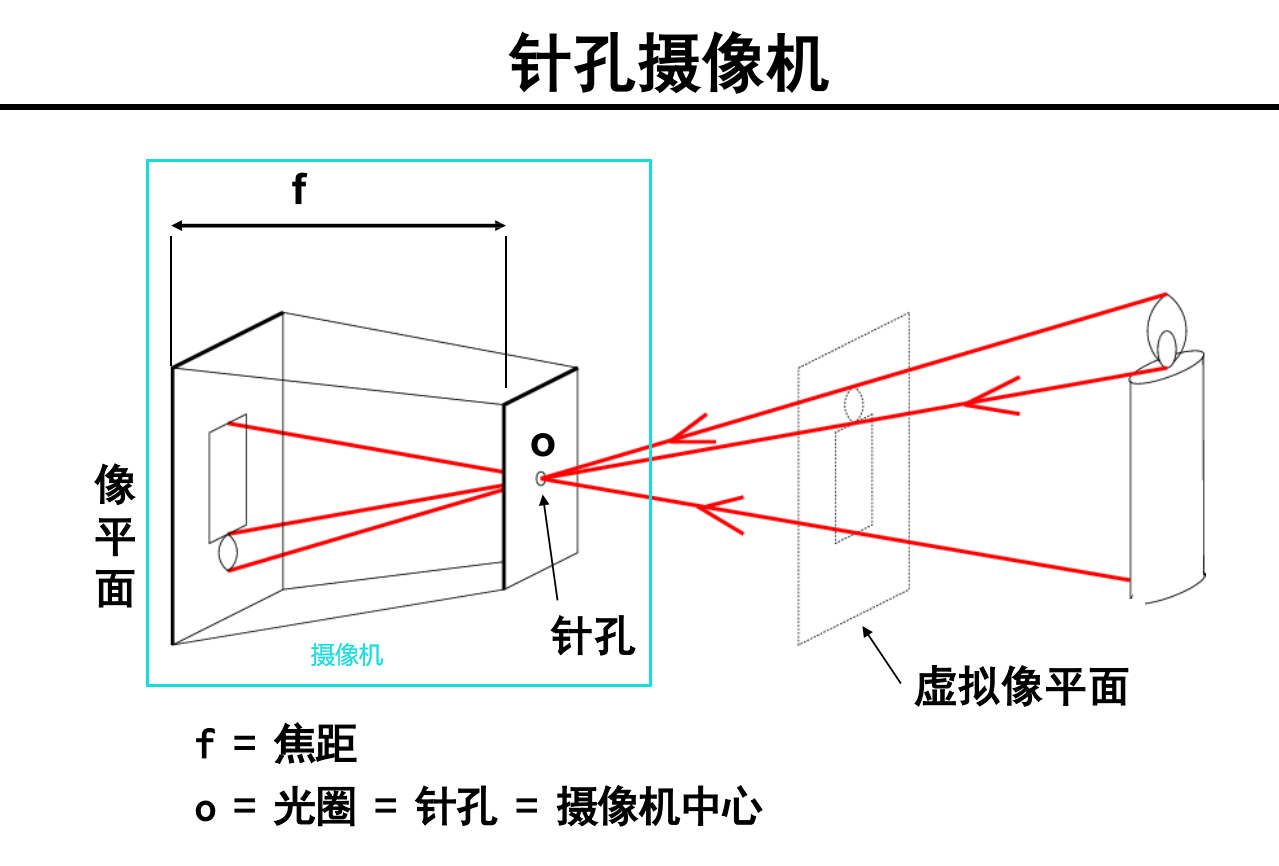
虚拟像平面(人为定义的):它与针孔的距离也是f,虚拟像平面是为了减少正负号的差异(像平面)带来的困扰

完成三维( P' )到二维( P )的映射:

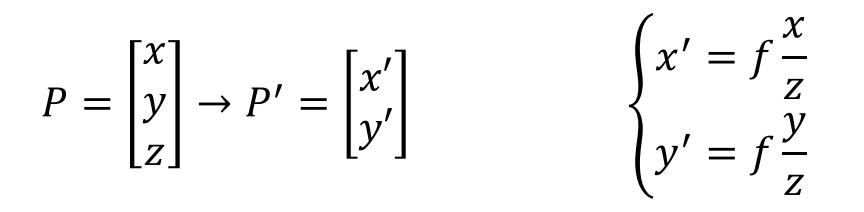
光圈的尺寸大小重要吗?
光圈(隔板的小孔太大)太大导致图像模糊

随着缩小光圈会越来越清晰,但是照片的会越来越暗,
怎么让成像越清晰还越亮呢?

增加透镜(透镜就相当于相机的镜头)

透镜的焦距与隔板到像平面的焦距不一样,注意区分
这里求x'与y'与之前求隔板到像平面的公式(相似三角形)一致,只不过这里将原来的z换成了现在的z'
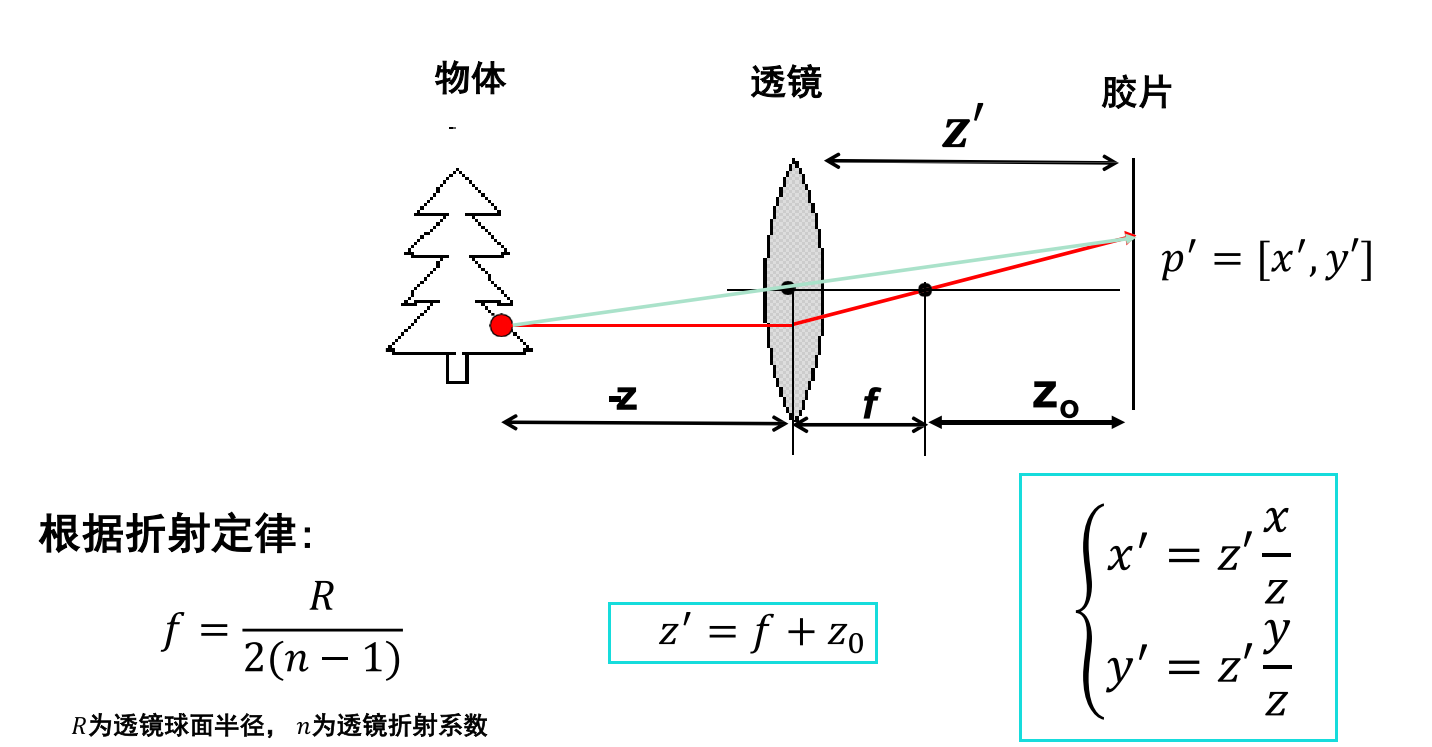
透镜问题:失焦


透镜问题:畸变

摄像机几何
像平面到像素平面
像平面(米)是中间状态,我们最终要的是像素平面(像素),最终要建模是三维世界与像素之间的关系而不是与像平面之间的关系
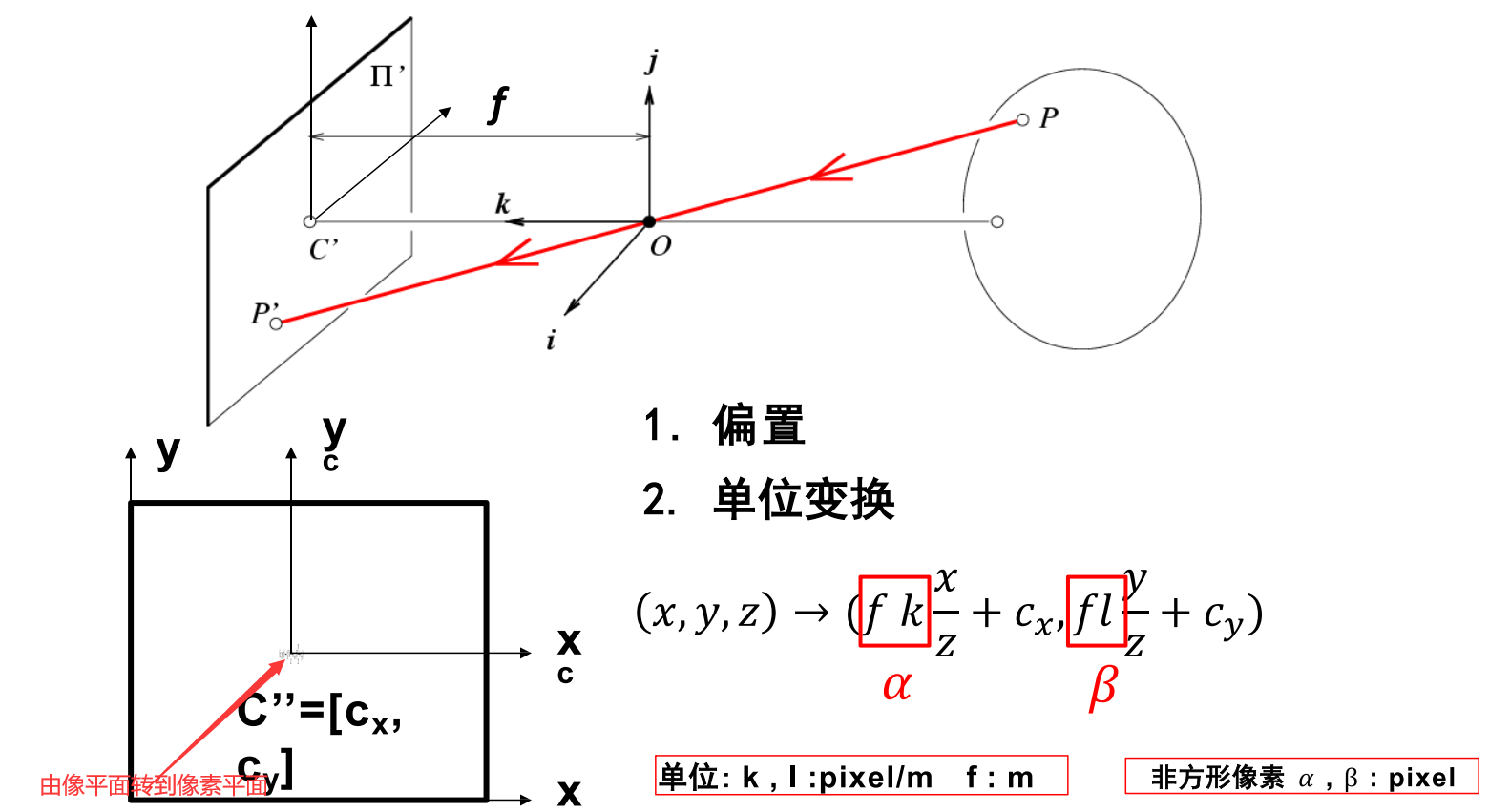

问题:P到P’的变换是线性的吗?
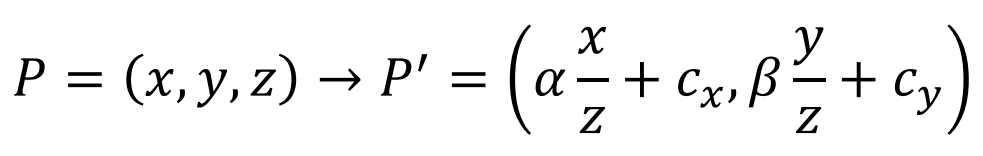
变换不是线性的,因为x、y、z都是不断变换的
欧式空间(二维)与齐次空间(三维)的转换:

那么如何将三维空间中的点与二维空间中点建立线性映射关系?
利用齐次与欧式的转换实现

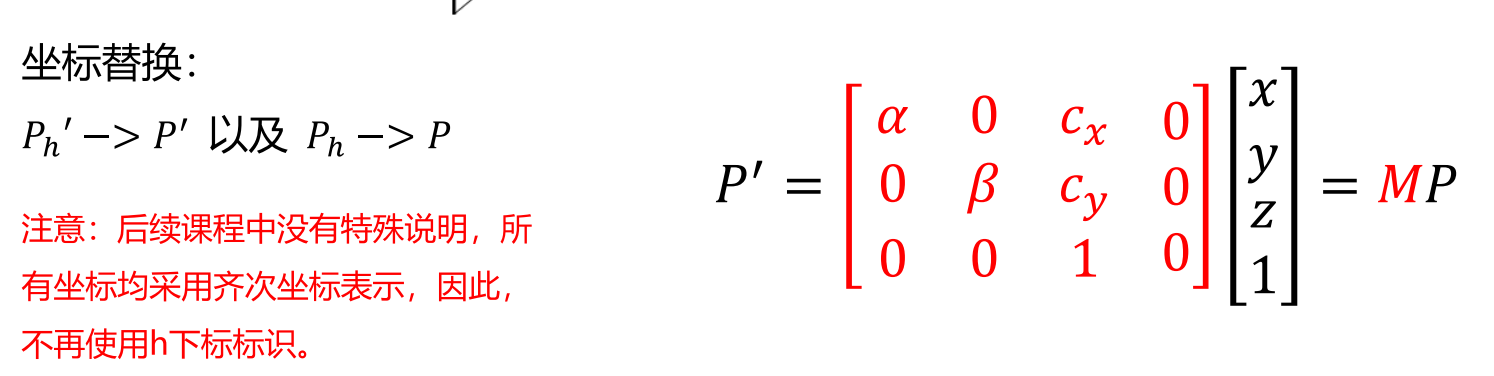
由于摄像机制作工艺的问题,会产生摄像机偏斜
也就是像平面到像素平面不是平行的,而会产生一个夹角

摄像机坐标到像素平面坐标的映射
要记住“投影矩阵”、“摄像机内参数矩阵”的概念
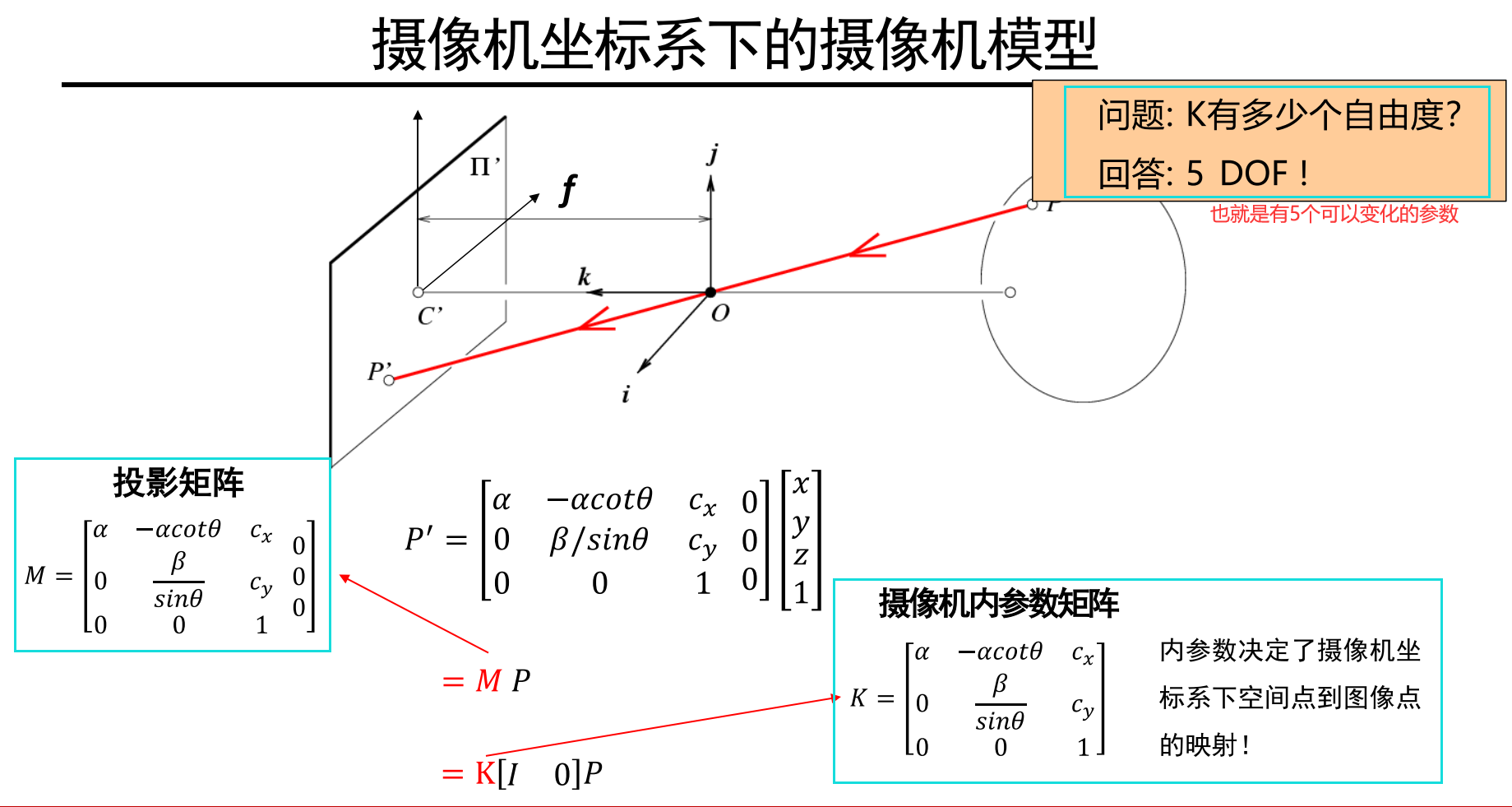
规范化摄像机
它不是真实存在的摄像机,它只是一种中间状态,我们以后用它推导一些性质什么的。
它们的中心和摄像机的中心重合,所以Cx和Cy都是0
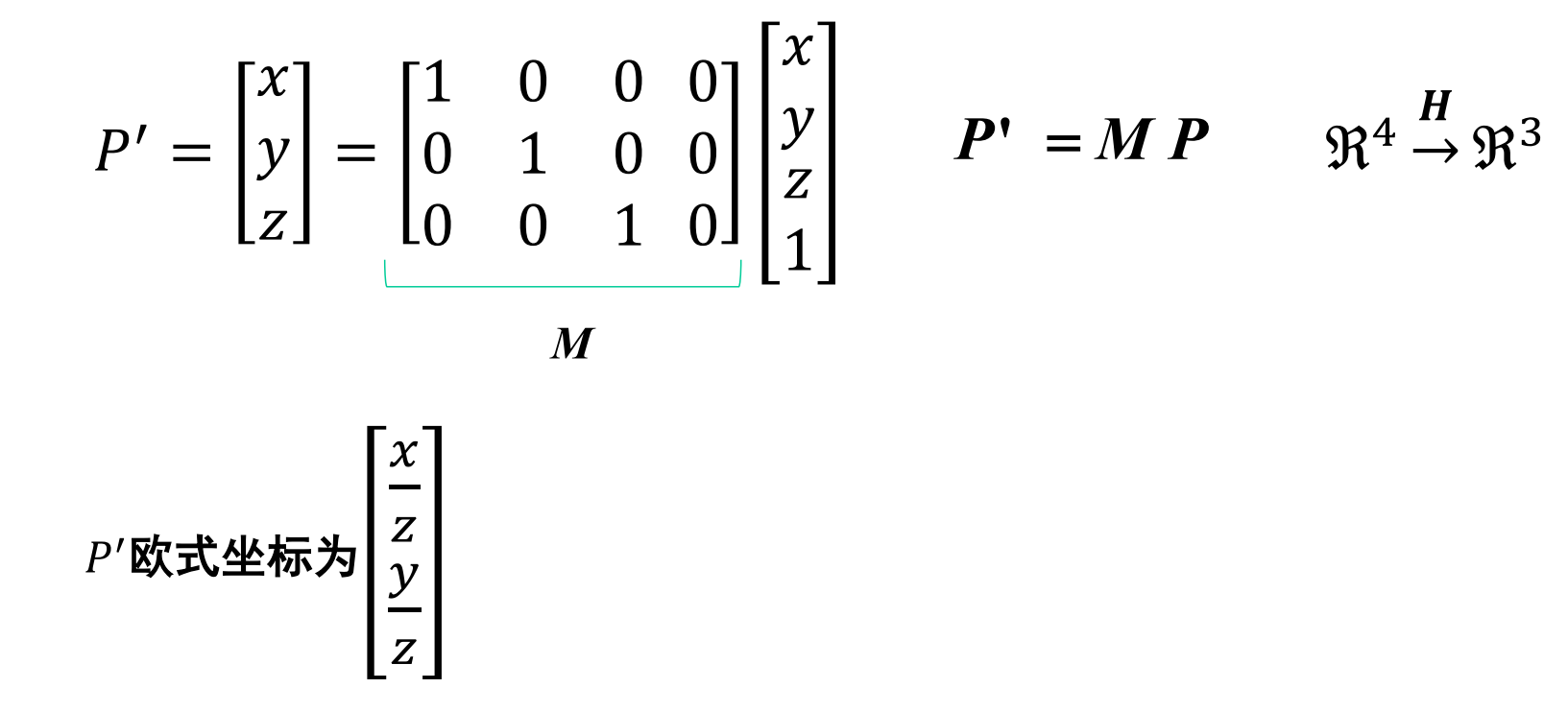
它的内参数矩阵是:单位矩阵
它有一个很重要的性质就是,可以直接由二维坐标添加一维变成三维坐标,也就是说我们知道了二维的坐标很容易就知道了三维空间下的坐标
世界坐标系
世界坐标系与摄像机坐标系的转换
将世界坐标系通过R(旋转)和T(平移)就可以转换为摄像机坐标系,R和T与摄像机的摆放位置有关
世界坐标系与像素平面的转换
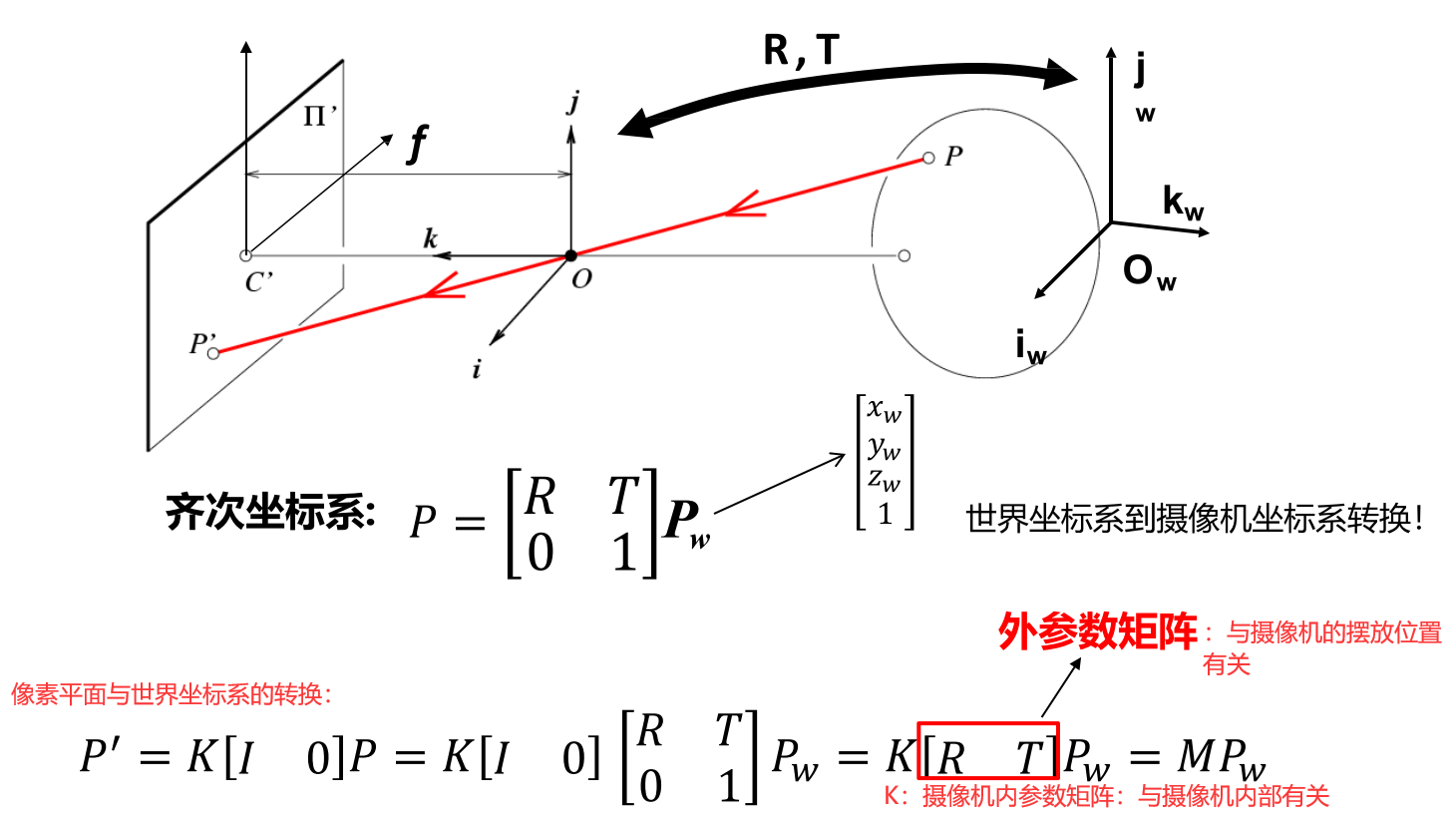
K:内参数矩阵:与摄像机内部构造有关
[R, T]:外参数矩阵:与摄像机的摆放位置有关
M:投影矩阵

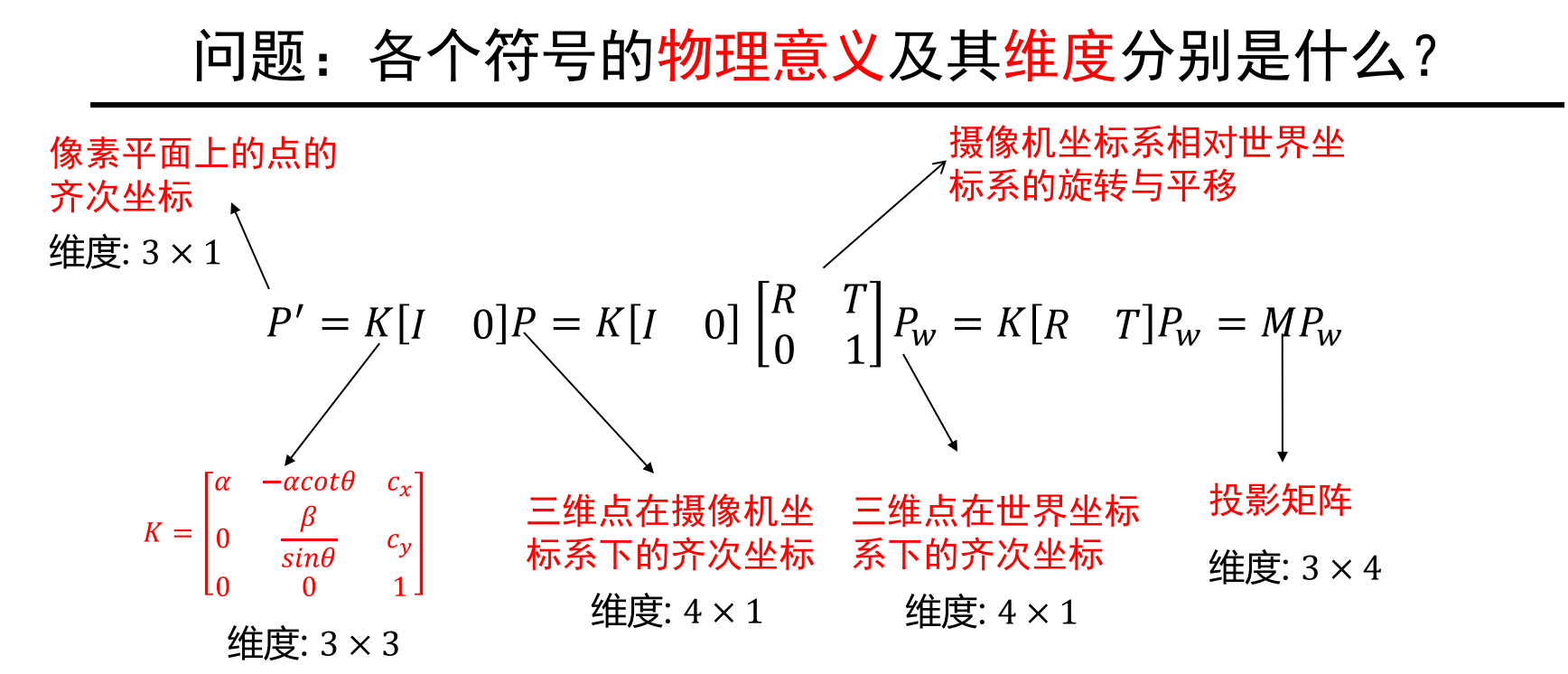
投影矩阵M有多少个自由度?

M有12个元素,但是有11个自由度
P’转为欧式坐标怎么转换?

其他摄像机模型
弱透视投影摄像机
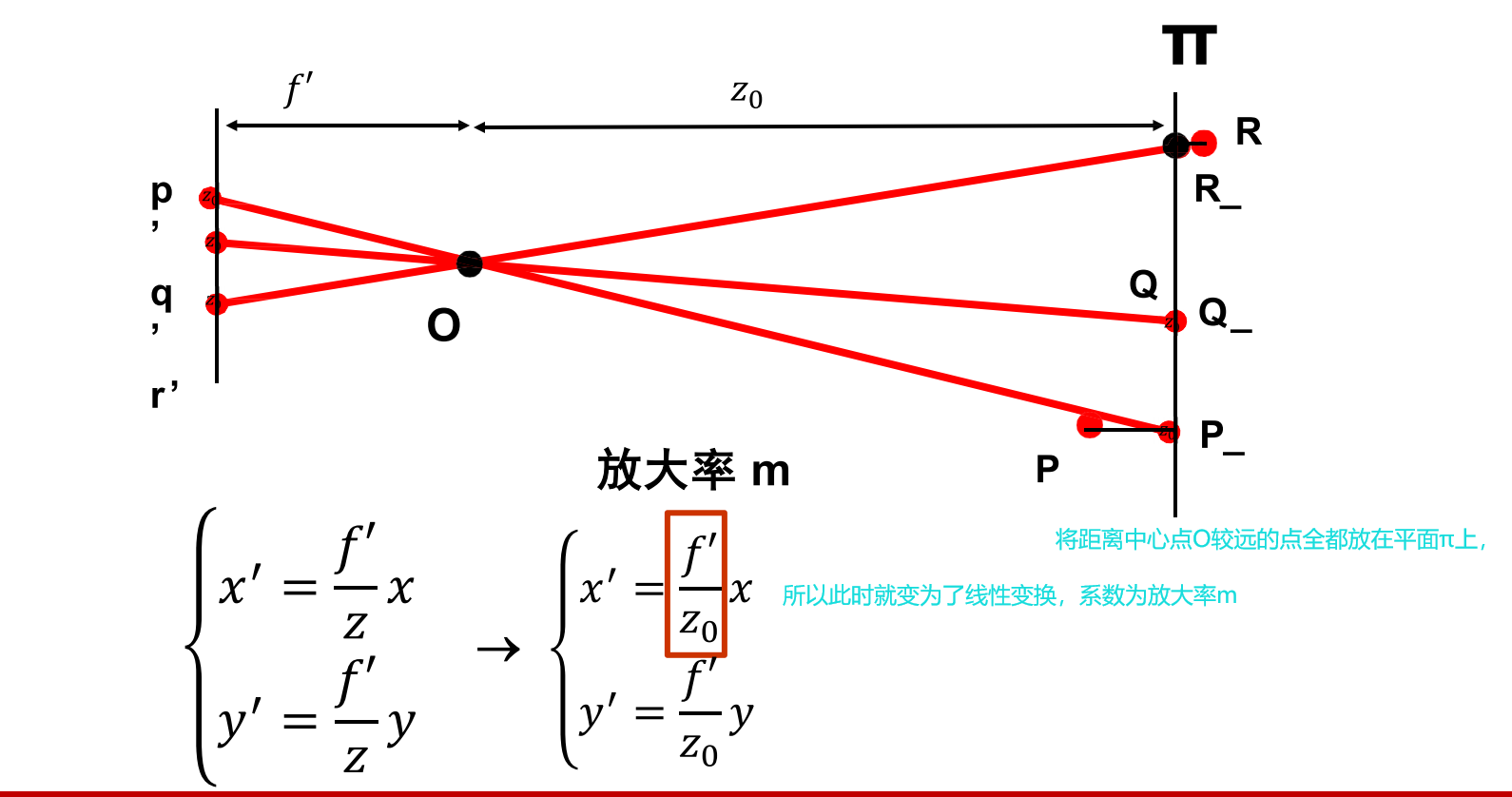
透视投影摄像机和弱透视投影摄像机

弱透视投影摄像机最后一行为【0,0,0,1】相当于忽略了物体的深度
正交投影摄像机

各种摄像机模型的应用场合
1、正交投影
-更多应用在建筑设计(AUTOCAD))或者工业设计行业
2、弱透视投影在数学方面更简单
-当物体较小且较远时准确,常用于图像识别任务
3、透视投影对于3D到2D映射的建模更为准确
-用于运动恢复结构或SLAM