【老生谈算法】matlab实现自适应对消器的LMS算法——LMS算法

基于LMS算法的自适应对消器的MATLAB实现

1．对消原理

信号，或者输出信号的均方值最小，就要求取得最小值，由(1-1)式推出等价的条件就是要求取得最小值，即要求输出信号与有用信号的误差的均方值为最小。
2．单个样本的仿真结果

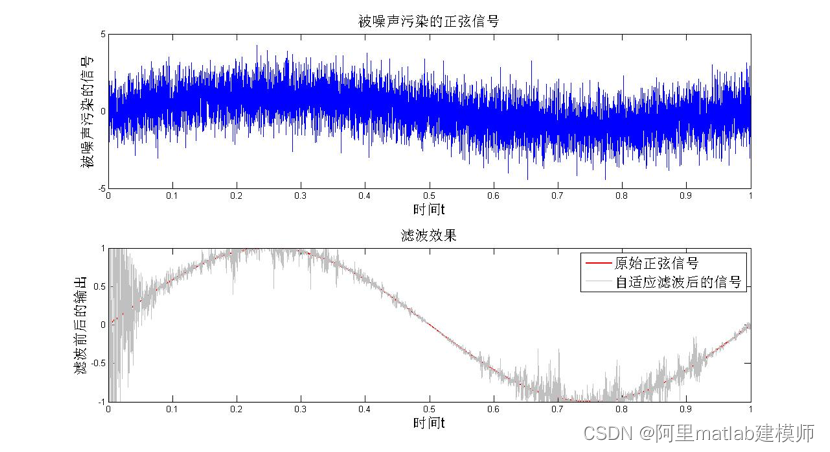
图2 对消噪声前后的效果图

MATLAB源代码如下：
%-------------------------------------------------
% 用LMS算法设计自适应滤波器
% 应用领域：自适应对消器
%-------------------------------------------------
clear all; clc;
delta = 1/10000;
t = 0:delta:1-delta;
t = t';                           % 转换成列向量
s = sin(2*pi*t);               
sigma_n0 = 1;
n0 = sigma_n0*randn(size(t));
x = s + n0;                  % 原始输入端的输入信号,为被噪声污染的正弦信号
d = x;                             % 对于自适应对消器，用x作为期望信号
n1 = n0;                   % 参考输入端的输入信号，为与n0相关的噪声

% 设计自适应滤波器
N = 5;                             % 滤波器阶数
w = ones(N,1);                      % 初始化滤波器权值
u = 0.0026;                         % 步长因子
y = zeros(length(t),1);
for k = N:length(t)
    y(k) = n1(k-N+1:k)'*w;
    e(k) = d(k) - y(k);                     
    w = w + 2*u*e(k).*n1(k-N+1:k);          % 跟新权值
end

% 图像化仿真效果
subplot(211),plot(t,x);title('被噪声污染的正弦信号');
subplot(212),plot(t,s,'k',t,e,'g');     % 对消噪声后，误差信号即为对原始信号的估计
legend('原始正弦信号','自适应滤波后的信号');
axis([0 1 -1 1]);title('滤波效果');

3．权值及误差样本均值的收敛性
由于LMS算法用单个样本误差来代替梯度法的误差均值，即用梯度的估计值代替梯度的精确值，这样算出的权值及误差将是随机变量，但权值的均值将收敛于梯度法算出的最优权值，均方误差也收敛于维纳解。
下面做出了100个样本的学习曲线可以观察其收敛情况。

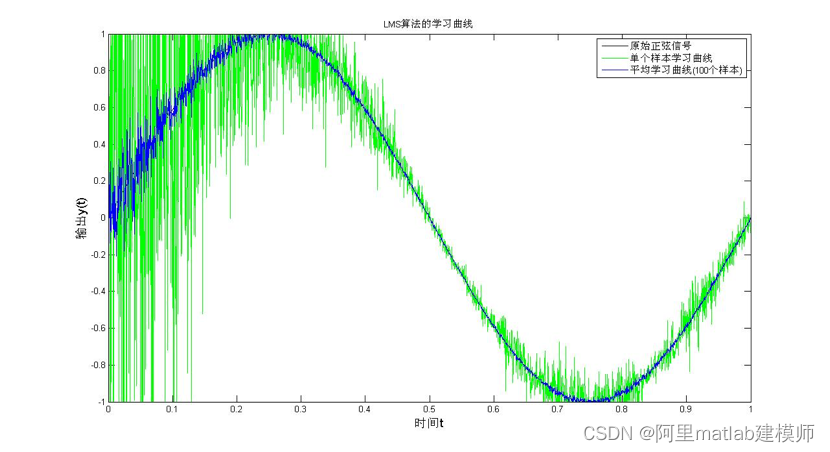
图3 LMS算法的学习曲线

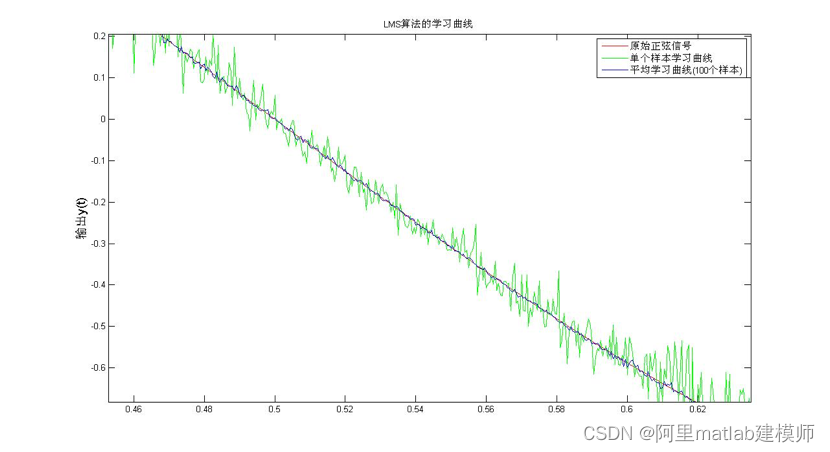
图4 LMS算法的学习曲线（局部放大图）
从图3和图4可以看出，相对于单个样本计算的误差也即滤波输出，100个样本计算的误差的均值与原始正弦信号更接近，这也验证了LMS算法计算的均方误差收敛于维纳解的理论。

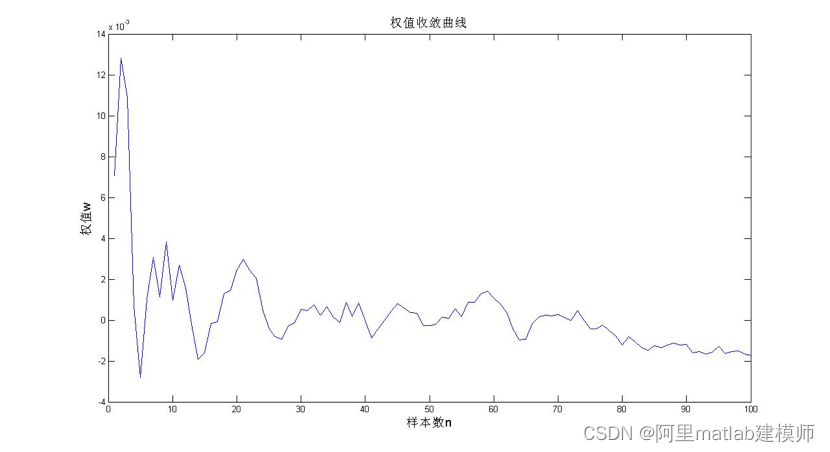
图5 权值的学习曲线
从图5 可以看出随着样本数的增加，权值波动越来越小，这也验证了LMS算法计算的权值的均值收敛于最优权值的理论。