基本粒子群算法的原理和matlab程序
一、粒子群算法的基本原理
粒子群优化算法源自对鸟群捕食行为的研究,最初由Kennedy和Eberhart提出,是一种通用的启发式搜索技术。
一群鸟在区域中随机搜索食物,所有鸟知道自己当前位置离食物多远,那么搜索的最简单有效的策略就是搜寻目前离食物最近的鸟的周围区域。PSO 算法利用这种模型得到启示并应用于解决优化问题。PSO 算法中,每个优化问题的解都是粒子在搜索空间中的位置,所有的粒子都有一个被优化的目标函数所决定的适应值,粒子还有一个速度值决定它们飞翔的方向和距离,然后粒子群就追随当前的最优粒子在解空间中搜索。
PSO 算法首先在给定的解空间中随机初始化粒子群,待优化问题的变量数决定了解空间的维数。每个粒子有了初始位置与初始速度。然后通过迭代寻优。在每一次迭代中,每个粒子通过跟踪两个“极值”来更新自己在解空间中的空间位置与飞翔速度。
第一个极值就是单个粒子本身在迭代过程中找到的最优解粒子,这个粒子叫做个体极值。另一个极值是种群所有粒子在迭代过程中所找到的最优解粒子,这个粒子是全局极值。上述的方法叫全局粒子群算法。如果不用种群所有粒子而只用其中一部分作为该粒子的邻居粒子,那么在所有邻居粒子中的极值就是局部极值,该方法称为局部 PSO 算法。
速度、位置的更新方程表示为:
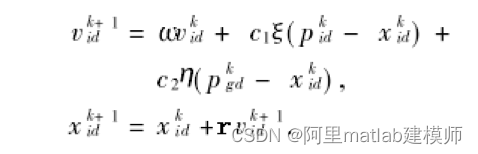
每个粒子自身搜索到的历史最优值 pi ,pi=(pi1,pi2,…,piQ),i=1,2,3,…,n。所有粒子搜索到的最优值pg,pg=(pg1,pg2,…,pgQ),注意这里的pg只有一个。
w1是保持原来速度的系数,所以叫做惯性权重。
c1是粒子跟踪自己历史最优值的权重系数,它表示粒子自身的认识,所以叫“认知”。通常设置为2。
c2是粒子跟踪群体最优值的权重系数,它表示粒子对整个群体知识的认识,所以叫做“社会知识”,经常叫做“社会”。通常设置为2。
& n是[0,1]区间内均匀分布的随机数。
是对位置更新的时候,在速度前面加的一个系数,这个系数我们叫做约束因子。通常设置为1。
粒子群优化算法的流程:
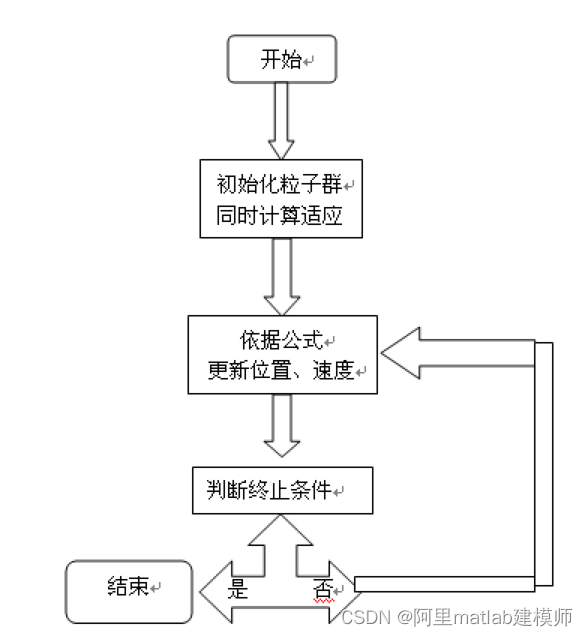
二、粒子群算法的matlab实现
主函数:
function [Result,OnLine,OffLine,MinMaxMeanAdapt]=PSO_Stand(SwarmSize,ParticleSize,ParticleScope,IsStep,IsDraw,LoopCount,IsPlot)
%输入参数:SwarmSize:种群大小的个数
%输入参数:ParticleSize:一个粒子的维数
%输入参数:ParticleScope:一个粒子在运算中各维的范围;
% ParticleScope格式:
% 3维粒子的ParticleScope格式:
% [x1Min,x1Max
% x2Min,x2Max
% x3Min,x3Max]
%输入参数:InitFunc:初始化粒子群函数
%输入参数:StepFindFunc:单步更新速度,位置函数
%输入参数:AdaptFunc:适应度函数
%输入参数:IsStep:是否每次迭代暂停;IsStep=0,不暂停,否则暂停。缺省不暂停
%输入参数:IsDraw:是否图形化迭代过程;IsDraw=0,不图形化迭代过程,否则,图形化表示。缺省不图形化表示
%输入参数:LoopCount:迭代的次数;缺省迭代100次
%输入参数:IsPlot:控制是否绘制在线性能与离线性能的图形表示;IsPlot=0,不显示;
% IsPlot=1;显示图形结果。缺省IsPlot=1
%返回值:Result为经过迭代后得到的最优解
%返回值:OnLine为在线性能的数据
%返回值:OffLine为离线性能的数据
%返回值:MinMaxMeanAdapt为本次完整迭代得到的最小与最大的平均适应度
[ParSwarm,OptSwarm]=InitSwarm(SwarmSize,ParticleSize,ParticleScope);%初始化粒子群
if IsStep~=0
disp('开始迭代,按任意键:')
pause
end
%开始更新算法的调用%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
for k=1:LoopCount
%显示迭代的次数:
disp('----------------------------------------------------------')
TempStr=sprintf('第 %g 次迭代',k);
disp(TempStr);
disp('----------------------------------------------------------')
%调用一步迭代的算法
[ParSwarm,OptSwarm]=BaseStepPso(ParSwarm,OptSwarm,ParticleScope,0.95,0.4,LoopCount,k);
figure(1);
plot(ParSwarm(:,1),ParSwarm(:,2),'g*','markersize',8);grid on;
XResult=OptSwarm(SwarmSize+1,1:ParticleSize);%存取本次迭代得到的全局最优值
YResult=AdaptFunc(XResult); %计算全局最优值对应的粒子的适应度值
if IsStep~=0
%XResult=OptSwarm(SwarmSize+1,1:ParticleSize);
%YResult=AdaptFunc(XResult);
str=sprintf('%g步迭代的最优目标函数值%g',k,YResult);
disp(str);
disp('下次迭代,按任意键继续');
pause
end
%记录每一步的平均适应度
MeanAdapt(1,k)=mean(ParSwarm(:,2*ParticleSize+1));%mean函数为取有效值函数
End
初始化函数:
function [ParSwarm,OptSwarm]=InitSwarm(SwarmSize,ParticleSize,ParticleScope)
%初始化粒子群矩阵,全部设为[0-1]随机数
%rand('state',0);
ParSwarm=rand(SwarmSize,2*ParticleSize+1);%初始化位置速度历史优化值
%对粒子群中位置,速度的范围进行调节
for k=1:ParticleSize
ParSwarm(:,k)=ParSwarm(:,k)*(ParticleScope(k,2)-ParticleScope(k,1))+ParticleScope(k,1);%调节速度,使速度与位置的范围一致
ParSwarm(:,ParticleSize+k)=ParSwarm(:,ParticleSize+k)*(ParticleScope(k,2)-ParticleScope(k,1))+ParticleScope(k,1);
end
%对每一个粒子计算其适应度函数的值
for k=1:SwarmSize
ParSwarm(k,2*ParticleSize+1)=AdaptFunc(ParSwarm(k,1:ParticleSize));%计算每个粒子的适应度值
end
%初始化粒子群最优解矩阵
OptSwarm=zeros(SwarmSize+1,ParticleSize);
%粒子群最优解矩阵全部设为零
[maxValue,row]=max(ParSwarm(:,2*ParticleSize+1));
%寻找适应度函数值最大的解在矩阵中的位置(行数)
OptSwarm=ParSwarm(1:SwarmSize,1:ParticleSize);
OptSwarm(SwarmSize+1,:)=ParSwarm(row,1:ParticleSize);%将适应度值最大的粒子的位置最为全局粒子的最优值
每步更新函数:
function [ParSwarm,OptSwarm]=BaseStepPso(ParSwarm,OptSwarm,ParticleScope,MaxW,MinW,LoopCount,CurCount)
%输入参数:ParSwarm:粒子群矩阵,包含粒子的位置,速度与当前的目标函数值
%输入参数:OptSwarm:包含粒子群个体最优解与全局最优解的矩阵
%输入参数:ParticleScope:一个粒子在运算中各维的范围;
%输入参数:AdaptFunc:适应度函数
%输入参数:AdaptFunc:适应度函数
%输入参数:MaxW MinW:惯性权重(系数)的最大值与最小值
%输入参数:CurCount:当前迭代的次数
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%线形递减策略(惯性权值的变化)
w=MaxW-CurCount*((MaxW-MinW)/LoopCount);
%得到粒子群群体大小以及一个粒子维数的信息
[ParRow,ParCol]=size(ParSwarm);
%得到粒子的维数
ParCol=(ParCol-1)/2;
SubTract1=OptSwarm(1:ParRow,:)-ParSwarm(:,1:ParCol);%求解出历史最优值与当前位置的差值
%*****更改下面的代码,可以更改c1,c2的变化*****
c1=2;
c2=2;
%完成一次粒子位置速度最优值的更新迭代
for row=1:ParRow
SubTract2=OptSwarm(ParRow+1,:)-ParSwarm(row,1:ParCol);%计算出全局最优值与当前该粒子位置的差值
%速度更新公式
TempV=w.*ParSwarm(row,ParCol+1:2*ParCol)+c1*unifrnd(0,1).*SubTract1(row,:)+c2*unifrnd(0,1).*SubTract2;
%限制速度的代码
for h=1:ParCol
if TempV(:,h)>ParticleScope(h,2)
TempV(:,h)=ParticleScope(h,2);
end
if TempV(:,h)<-ParticleScope(h,2)
TempV(:,h)=-ParticleScope(h,2)+1e-10;%加1e-10防止适应度函数被零除
end
end
%更新该粒子速度值
ParSwarm(row,ParCol+1:2*ParCol)=TempV;
%*****更改下面的代码,可以更改约束因子的变化*****
a=0.729;%约束因子
%位置更新公式
TempPos=ParSwarm(row,1:ParCol)+a*TempV;
%限制位置范围的代码
for h=1:ParCol
if TempPos(:,h)>ParticleScope(h,2)
TempPos(:,h)=ParticleScope(h,2);
end
if TempPos(:,h)<=ParticleScope(h,1)
TempPos(:,h)=ParticleScope(h,1)+1e-10;%加1e-10防止适应度函数被零除
end
end
%更新该粒子位置值
ParSwarm(row,1:ParCol)=TempPos;
%计算每个粒子的新的适应度值
ParSwarm(row,2*ParCol+1)=AdaptFunc(ParSwarm(row,1:ParCol));
if ParSwarm(row,2*ParCol+1)>AdaptFunc(OptSwarm(row,1:ParCol))
OptSwarm(row,1:ParCol)=ParSwarm(row,1:ParCol);
end
end
%寻找适应度函数值最大的解在矩阵中的位置(行数),进行全局最优值的改变
[maxValue,row]=max(ParSwarm(:,2*ParCol+1));
if AdaptFunc(ParSwarm(row,1:ParCol))>AdaptFunc(OptSwarm(ParRow+1,:))
OptSwarm(ParRow+1,:)=ParSwarm(row,1:ParCol);
End
适应度函数:
function y=AdaptFunc(x)
这个需要针对不同的问题,自己编写;
End
只要将上面的函数保存到matlab可搜索路径中,即可调用该函数,使用函数的数据格式即可,例如:PSO_Stand(50,2,[0,1;0,1],1),粒子群数目,目标函数的变量数目,变量的范围值,之后的是显示和应用的函数,参考着程序进行精简即可。