【数据结构与算法】- 栈+队列

企业开发 2022-06-24 17:28
0 阅读

目录

1.假设以I和O分别表示入栈和出栈操作。栈的初始状态和最终状态均为空，入栈和出栈的操作序列可表示为仅由I和O组成的序列，可以操作的序列称为合法序列，否则称为非法序列。

设计一个算法，判断给定的操作序列 IOIIOIOO 和 IOOIOIIO 是否合法。

2.设单链表的表头指针为L，结点结构由data和next两个域组成，其中data域为字符型。试着设计算法判断该链表的全部n个字符是否中心对称，例如xyx，xyyx都是中心对称

3.设有两个栈s1，s2，都采用顺序栈方式，并共享一个存储区[0,maxsize-1]，为了尽量利用空间。减少溢出的可能，可以采用栈顶相向，迎面增长的存储方式，试着设计s1与s2有关入栈和出栈的操作算法。

4.若希望循环队列中的元素都能得到利用，则需设置一一个标志域tag,并以tag的值为0或1来区分队头指针front和队尾指针rear相同时的队列状态是“空”还是“满”。试编写与此结构相应的入队和出队算法。

5.Q是一个队列，S是一个空栈，实现将队列中的元素逆置的算法。 

6.利用两个栈S1,S2来模拟一个队列，已知栈的4个运算定义如下: 

 7.假设一个算术表达式中包含圆括号，方括号，花括号3种类型的括号。编写一个算法来判别括号是否匹配。

8.按下图所示铁道进行车厢调度(注意，两侧铁道均为单向行驶道，火车调度站有一个用于调度的“栈道”)， 火车调度站的入口处有n节硬座和软座车厢(分别用H和S表示)等待调度，试编写算法，输出对这n节车厢进行调度的操作(即入栈或出栈操作)序列，以使所有的软座车厢都被调整到硬座车厢之前。

9.利用一个栈来实现以下递归函数的非递归计算。

扫描二维码关注公众号，回复： 14318393 查看本文章

10.某汽车轮渡口， 过江渡船每次能载10辆车过江。过江车辆分为客车类和货车类，上渡船有如下规定:同类车先到先上船;客车先于货车上船，且每上4辆客车，才允许放上1辆货车;若等待客车不足4辆，则以货车代替;若无货车等待，允许客车都上船。试设计一个算法模拟渡口管理。

1.假设以I和O分别表示入栈和出栈操作。栈的初始状态和最终状态均为空，入栈和出栈的操作序列可表示为仅由I和O组成的序列，可以操作的序列称为合法序列，否则称为非法序列。

设计一个算法，判断给定的操作序列 IOIIOIOO 和 IOOIOIIO 是否合法。

//判断序列是否合法
#include<iostream>
using namespace std;
int n;
bool isok(char s[])
{
    int I=0,O=0;
    for(int i=0;i<n;i++)
    {
        if(s[i]=='I') I++;
        else O++;
        if(O>I) return false;
    }
    if(O==I) return true;
    return false;
}
int main()
{
    char s[8]={'I','O','O','I','O','I','I','O'};
    n=8;
    if(isok(s)) cout<<"合法"<<endl;
    else cout<<"不合法"<<endl;
    return 0;
}

2.设单链表的表头指针为L，结点结构由data和next两个域组成，其中data域为字符型。试着设计算法判断该链表的全部n个字符是否中心对称，例如xyx，xyyx都是中心对称

//判断链表是否是中心对称的
#include<iostream>
using namespace std;
typedef struct lnode{
    char data;
    struct lnode *next;
}lnode,*linklist;
char s1[5]={'x','y','z','y','x'};
//int n=4;
void buildlist(linklist &L)
{
    L=(linklist)malloc(sizeof(lnode));
    lnode *s,*r=L;
    for(int i=0;i<5;i++)
    {
        s=(lnode *)malloc(sizeof(lnode));
        s->data=s1[i];
        r->next=s;
        r=r->next;
    }
    r->next=NULL;
}
bool isok(linklist L,int n)
{
    char str[5/2];
    lnode *p=L->next;
    int i;
    for(i=0;i<5/2;i++)
    {
        str[i]=p->data;
        p=p->next;
    }
    i--;
    if(5%2!=0) p=p->next;
    while(p&&p->data==str[i])
    {
        i--;
        p=p->next;
    }
    if(i==-1) return true;
    return false;
}
int main()
{
    linklist L;
    buildlist(L);
    if(isok(L,5)) cout<<"yes"<<endl;
    else cout<<"no"<<endl;
    return 0;
}

3.设有两个栈s1，s2，都采用顺序栈方式，并共享一个存储区[0,maxsize-1]，为了尽量利用空间。减少溢出的可能，可以采用栈顶相向，迎面增长的存储方式，试着设计s1与s2有关入栈和出栈的操作算法。

//两栈共享一片内存 分别进行进栈和出栈操作
#include<iostream>
using namespace std;
#define Max 50
typedef struct{
    int data[Max];
    int top[2];
}stack1;
stack1 s;
int push(int i,int x)
{
    if(i!=0&&i!=1){
        cout<<"无栈"<<endl;
        return -1;
    }
    if(s.top[1]-s.top[0]==1) {
        cout<<"栈满"<<endl;
        return -1;
    }
    if(i==0)
    {
        s.data[++s.top[0]]=x;
    }
    else s.data[--s.top[1]]=x;
    return 1;
}
int pop(int i)
{
    if(i!=0&&i!=1)
    {
        cout<<"无栈"<<endl;
    }    
    if(i==0)
    {
        if(s.top[0]==-1)
        {
            cout<<"0号栈栈空"<<endl;
            return -1;
        }
        return s.data[s.top[0]--];
    }
    else
    {
        if(s.top[1]==Max)
        {
            cout<<"1号栈栈空"<<endl;
            return -1;
        }
        return s.data[s.top[1]++];
    }
}

int main()
{
    s.top[0]=-1,s.top[1]=Max;
    if(push(0,1)!=-1) cout<<"0号栈进栈成功"<<endl;
    int x=pop(0);
    if(x!=-1) {
        cout<<"0号栈出栈成功  ";
        cout<<"0号栈出栈元素为: "<<x<<endl;}

    int y=pop(0);
    return 0;
}

4.若希望循环队列中的元素都能得到利用，则需设置一一个标志域tag,并以tag的值为0或1来区分队头指针front和队尾指针rear相同时的队列状态是“空”还是“满”。试编写与此结构相应的入队和出队算法。

//循环队列 tag
#include<iostream>
using namespace std;
#define Max 10
typedef struct{
    int data[Max];
    int f,r,tag;
}squeue;
bool enters(squeue &s,int x)
{
    if(s.f==s.r&&s.tag==1) 
    {
        cout<<"队满 进队失败"<<endl;
        return false;
    }
    s.data[s.r]=x;
    cout<<s.data[s.r]<<" ";
    s.r=(s.r+1)%Max;
    s.tag=1;
    return true;
}
int outs(squeue &s,int x)
{
    if(s.f==s.r&&s.tag==0)
    {
        cout<<"队空 出队失败"<<endl;
        return 0;
    }
    x=s.data[s.f];
    s.f=(s.f+1)%Max;
    s.tag=0;
    return 1;
}
int main()
{
    squeue s;
    s.f=0,s.r=0,s.tag=0;
	int i;
    for(i=0;i<10;i++)
    {
        enters(s,i);
    }
    cout<<endl;
    enters(s,1);
    int x=0;
    for(i=0;i<10;i++)
    {
        outs(s,x);
    }
    outs(s,x);
    return 0;
}

5.Q是一个队列，S是一个空栈，实现将队列中的元素逆置的算法。 

//队列逆置通过辅助栈
#include<iostream>
using namespace std;
#define Max 10
struct stack1{
    int data[Max];
    int top;
};
struct squeue1{
    int data[Max];
    int r,f,tag;
};
bool entersqueue(squeue1 &s,int x)
{
    if(s.f==s.r&&s.tag==1)
    {
        cout<<"队满 进队失败"<<endl;
        return false;
    }
    s.data[s.r]=x;
    s.r=(s.r+1)%Max;
    s.tag=1;
    return true;
}
int outsqueue1(squeue1 &s,int &x)
{
    if(s.f==s.r&&s.tag==0)
    {
        cout<<"队空 出队失败"<<endl;
        return 0;
    }
    x=s.data[s.f];
    s.f=(s.f+1)%Max;
    s.tag=0;
    return 1;
}
bool enterstack(stack1 &s,int x)
{
    if(s.top==Max-1)
    {
        cout<<"栈满 进栈失败"<<endl;
        return false;
    }
    s.data[++s.top]=x;
    return true;
}
int outstack(stack1 &s,int &x)
{
    if(s.top==-1)
    {
        cout<<"栈空 出栈失败"<<endl;
        return 0;
    }
    x=s.data[s.top--];
    return 1;
}
void disp(squeue1 s)
{
    for(int i=0;i<Max;i++)
    {
        cout<<s.data[s.f]<<" ";
        s.f=(s.f+1)%Max;
    }
    cout<<endl;
}
int main()
{
    squeue1 s1;
    stack1 s2;
    s1.f=0,s1.r=0,s1.tag=0;
    s2.top=-1;
    for(int i=0;i<Max;i++)
    {
        entersqueue(s1,i);
    }
    disp(s1);
    int x=0;
    while(!(s1.f==s1.r&&s1.tag==0))
    {
        outsqueue1(s1,x);
        enterstack(s2,x);
    }
    while(!(s2.top==-1))
    {
        outstack(s2,x);
        entersqueue(s1,x);
    }
    disp(s1);
    return 0;
}

6.利用两个栈S1,S2来模拟一个队列，已知栈的4个运算定义如下: 

如何运用栈的运算来实现该队列的3个运算？

//用栈模拟队列的进栈出栈判空操作
#include<iostream>
using namespace std;
#define Max 10
struct stack1{
    int data[Max];
    int top;
};
bool isempty(stack1 s)
{
    if(s.top==-1) return true;
    return false;
}
bool isfull(stack1 s)
{
    if(s.top==Max-1) return true;
    return false;
}
bool enterstack(stack1 &s,int x)
{
    if(isfull(s)) return false;
    s.data[++s.top]=x;
    return true;
}
int outstack(stack1 &s,int &x)
{
    if(isempty(s)){
        cout<<"栈空"<<endl;
        return 0;
    }
    x=s.data[s.top--];
    return 1;
}
void disp(stack1 &s)
{
  int top1=s.top;
  while(top1!=-1)
  {
      cout<<s.data[top1]<<" ";
      top1--;
  }
  cout<<endl;
}
int entersqueue(stack1 &s1,stack1 &s2,int x)
{
    if(!isfull(s1))
    {
        enterstack(s1,x);
        return 1;
    }
    else if(isfull(s1)&&!isempty(s2))
    {
        cout<<"队满"<<endl;
        return 0;
    }
    if(isfull(s1)&&isempty(s2))
    {
        while(!isempty(s1))
        {
            outstack(s1,x);
            enterstack(s2,x);
        }
    }
    enterstack(s1,x);
    return 1;
}
void outsqueue(stack1 &s1,stack1 &s2,int &x)
{
    if(!isempty(s2))
    {
        outstack(s2,x);
    }
    else if(isempty(s1))
    {
        cout<<"栈空"<<endl;
    }
    else{
        while(!isempty(s1))
        {
            outstack(s1,x);
            enterstack(s2,x);
        }
        outstack(s2,x);
    }
}
int main()
{
    stack1 s1,s2;
    s1.top=-1,s2.top=-1;
    for(int i=0;i<Max;i++)
    {
        enterstack(s1,i);
    }
    cout<<"出栈顺序(先进后出)s1(队列是先进先出)"<<" "<<endl;
    int x=0;
    disp(s1);
    outsqueue(s1,s2,x);
    cout<<"出队元素第一个元素x="<<x<<endl;
    disp(s2);
    return 0;
}

 7.假设一个算术表达式中包含圆括号，方括号，花括号3种类型的括号。编写一个算法来判别括号是否匹配。

//括号匹配问题
#include<iostream>
using namespace std;
#define Max 10
struct stack1{
    char data[Max+1];
    int top;
};
bool isempty(stack1 s)
{
    if(s.top==-1) return true;
    return false;
}
bool isfull(stack1 s)
{
    if(s.top==Max-1) return true;
    return false;
}
bool enterstack(stack1 &s,char x)
{
    if(isfull(s))
    {
        cout<<"栈满"<<endl;
        return false;
    }
    s.data[++s.top]=x;
    return true;
}
int outstack(stack1 &s,char &x)
{
    if(isempty(s))
    {
        cout<<"栈空"<<endl;
        return 0;
    }
    x=s.data[s.top--];
    return 1;
}
bool isright(char *str)
{
    stack1 s;
    s.top=-1;
    int i=0;
    char ans;
    while(str[i]!='\0')
    {
        if(str[i]=='('||str[i]=='['||str[i]=='{')   enterstack(s,str[i]);
        else if(str[i]==')')
        {
            outstack(s,ans);
            if(ans!='(') return false;
        }
        else if(str[i]==']')
        {
            outstack(s,ans);
            if(ans!='[') return false;
        }
        else if(str[i]=='}')
        {
             outstack(s,ans);
            if(ans!='{') return false;
        }
        i++;
    }
    if(isempty(s)) return true;
    return false;
}
int main()
{
    char *str=(char*)"()[](}{}()";
    cout<<str<<endl;
    if(!isright(str)) cout<<"括号不匹配"<<endl;
    else cout<<"括号匹配"<<endl;
    return 0;
}

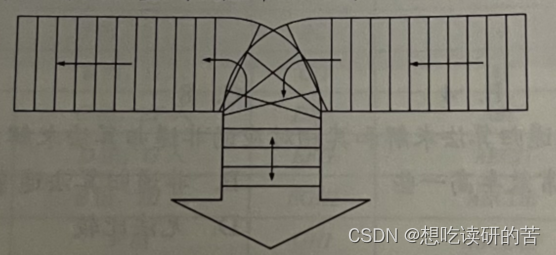
8.按下图所示铁道进行车厢调度(注意，两侧铁道均为单向行驶道，火车调度站有一个用于调度的“栈道”)， 火车调度站的入口处有n节硬座和软座车厢(分别用H和S表示)等待调度，试编写算法，输出对这n节车厢进行调度的操作(即入栈或出栈操作)序列，以使所有的软座车厢都被调整到硬座车厢之前。

//栈的运用
#include<iostream>
using namespace std;
#define Max 10
struct stack1{
    char data[Max];
    int top;
};
bool isempty(stack1 s)
{
    if(s.top==-1)return true;
    return false;
}
bool isfull(stack1 s)
{
    if(s.top==Max-1) return true;
    return false;
}
bool enterstack(stack1 &s,char x)
{
    if(isfull(s))
    {
        cout<<"栈满"<<endl;
        return false;
    }
    s.data[++s.top]=x;
    return true;
}
void outstack(stack1 &s,char &x)
{
    if(isempty(s))
    {
        cout<<"栈空"<<endl;
    }
    else
    {
        x=s.data[s.top--];
    }
}
void Sort(char str[])
{
    stack1 s;
    s.top=-1;
    char ans[Max+1];
    int j=0;
    for(int i=0;i<Max;i++)
    {
        if(str[i]=='H') enterstack(s,str[i]);
        else ans[j++]=str[i];
    }
    char c;
    while(!isempty(s))
    {
        outstack(s,c);
        ans[j++]=c;
    }
    for(i=0;i<Max;i++)
        cout<<ans[i];
        cout<<endl;
}
int main()
{
    char str[Max+1]="HSHSHHHSHS";
    cout<<str<<endl;
    Sort(str);
    return 0;
}

9.利用一个栈来实现以下递归函数的非递归计算。

 

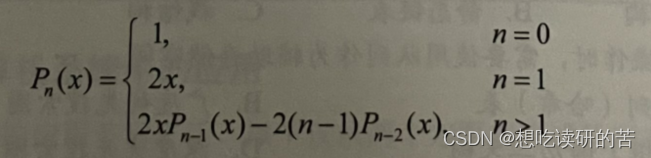
以n=0为例

以n=1为例

以n=2(n>1)为例

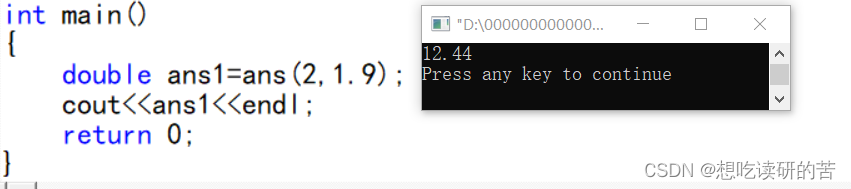
以n=3(n>1)为例

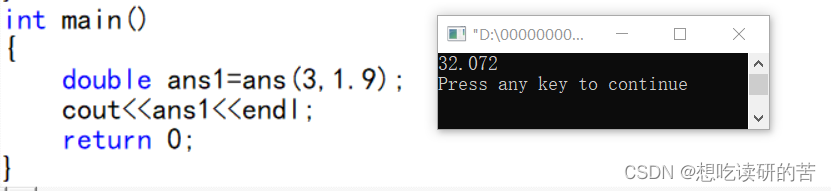
10.某汽车轮渡口， 过江渡船每次能载10辆车过江。过江车辆分为客车类和货车类，上渡船有如下规定:同类车先到先上船;客车先于货车上船，且每上4辆客车，才允许放上1辆货车;若等待客车不足4辆，则以货车代替;若无货车等待，允许客车都上船。试设计一个算法模拟渡口管理。

//队列的应用
#include<iostream>
using namespace std;
#define Max 10
struct squeue{
    int data[Max];
    int f,r,tag;
};
bool isempty(squeue s)
{
    if(s.f==s.r&&s.tag==0) return true;
    return false;
}
bool isfull(squeue s)
{
    if(s.f==s.r&&s.tag==1) return true;
    return false;
}
bool entersqueue(squeue &s,int x)
{
    if(isfull(s)) return false;
    s.data[s.r]=x;
    s.r=(s.r+1)%Max;
    s.tag=1;
    return true;
}
bool outsqueue(squeue &s,int &x)
{
   if(isempty(s)) return false;
   x=s.data[s.f];
   s.f=(s.f+1)%Max;
   s.tag=0;
   return true;
}
void disp(squeue &s)
{
    while(!isempty(s))
    {
        cout<<s.data[s.f]<<" ";
        s.f=(s.f+1)%Max;
        s.tag=0;
    }
    cout<<endl;
}
void car()
{
    squeue ans,k,h;
    ans.f=ans.r=0;ans.tag=0;
    k.f=k.r=0;k.tag=0;
    h.f=h.r=0;h.tag=0;
	int i;
    for(i=0;i<Max;i++)
    {
        entersqueue(k,1);
        entersqueue(h,2);
    }
    int j=0,x;
    while(j<10)
    {
        if(!isempty(k)&&i<4)
        {
            outsqueue(k,x);
            entersqueue(ans,x);
            i++;j++;
        }
        else if(i==4&&!isempty(h))
        {
            outsqueue(h,x);
            entersqueue(ans,x);
            j++;i=0;
        }
        else
        {
            while(j<10&&i<4&&isempty(h))
            {
                outsqueue(h,x);
                entersqueue(ans,x);
                i++;j++;
            }
            i=0;
        }
        if(isempty(k)&&isempty(h)) j=11;
    }
    cout<<"客车队列"<<endl;// 1 1 1 1 1 1 1 1 1 1 
    disp(k);
    cout<<"货车队列"<<endl;// 2 2 2 2 2 2 2 2 2 2
    disp(h);
    cout<<"目标队列(客车两组4个1(这两组分别搭配)--货车的两个2)"<<endl;
    disp(ans);

}
int main()
{
    car();
    return 0;
}

猜你喜欢

目录

热门文章