【王道数据结构编程题】- 链表算法题

目录

19. 设有一个带头结点的循环单链表，其结点值均为正整数。设计一个算法，反复找出单链表中结点值最小的结点并输出，然后将该结点从中删除，直到单链表空为止，再删除表头结点。

20.设头指针为L的带有表头结点的非循环双向链表，其每个结点中除有pred(前驱指针)、data (数据)和next (后继指针)域外，还有一个访问频度域freq。在链表被启用前，其值均初始化为零。每当在链表中进行一-次Locate(L,x)运算时，令元素值为x的结点中freq域的值增1,并使此链表中结点保持按访问频度非增(递减)的顺序排列，同时最近访问的结点排在频度相同的结点前面，以便使频繁访问的结点总是靠近表头。试编写符合上述要求的Locate (L,x)运算的算法，该运算为函数过程，返回找到结点的地址，类型为指针型。

21.单链表有环，是指单链表的最后一个结点的指针指向了链表中的某个结点(通常单链表的最后一个结点的指针域是空的)。试编写算法判断单链表是否存在环。

22.已知一个带有表头结点的单链表，结点结构为 data link

假设该链表只给出了头指针list. 在不改变链表的前提下，请设计一个尽可能高效的算法，查找链表中倒数第k个位置上的结点(k为正整数)。若查找成功，算法输出该结点的data域的值，并返回1;否则，只返回0。

23.假定采用带头结点的单链表保存单词，当两个单词有相同的后缀时，可共享相同的后缀存储空间，例如，"loading" 和"being" 的存储映像如下图所示。

 24.用单链表保存m个整数，结点的结构为[data][link], 且  I data l < n(n为正整数)。现要求设计一个时间复杂度尽可能高效的算法，对于链表中data的绝对值相等的结点，仅保留第一次出现的结点而删除其余绝对值相等的结点。

25.设线性表L=(a1,a2,a3,...,an-2,an-1,an)，采用带头节点的单链表保存。设计算法，重新排列L中的节点，得到线性表L'=(a1,an,a2,an-1,a3,an-2,...)。

---

其他-王道数据结构算法题-链表题，如下

【王道数据结构编程题】- 链表代码题

【王道数据结构编程题】- 链表编程题 

19. 设有一个带头结点的循环单链表，其结点值均为正整数。设计一个算法，反复找出单链表中结点值最小的结点并输出，然后将该结点从中删除，直到单链表空为止，再删除表头结点。

代码实现：

//循环单链表依次输出最小值并删除节点
#include<iostream>
using namespace std;
typedef struct lnode{
    int data;
    struct lnode *next;
}lnode,*linklist;
int a[5]={3,5,2,7,1};
int n=5;
void buildlist(linklist &L)
{
    L=(linklist)malloc(sizeof(lnode));
    lnode *s,*r=L;
    for(int i=0;i<n;i++)
    {
        s=(lnode *)malloc(sizeof(lnode));
        s->data=a[i];
        r->next=s;
        r=r->next;
    }
    r->next=L;
}
void disp(linklist L)
{
    lnode *s=L->next;
    while(s!=L)
    {
        cout<<s->data<<" ";
        s=s->next;
    }
    cout<<endl;
}
void deletelist(linklist &L)
{
    lnode *p,*r,*min,*mp;
    while(L->next!=L)
    {
        p=L->next,r=L,min=p,mp=r;
        while(p!=L)
        {
            if(p->data<min->data)
            {
                min=p;
                mp=r;
            }
            else
            {
                r=p;
                p=p->next;
            }
        }
        cout<<min->data<<" ";
        mp->next=min->next;
        free(min);
    }
    free(L);
}
int main()
{
    linklist L;
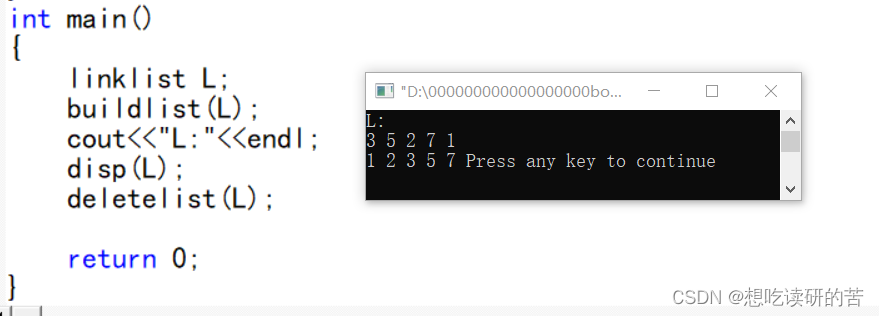
    buildlist(L);
    cout<<"L:"<<endl;
    disp(L);
    deletelist(L);
    
    return 0;
}

20.设头指针为L的带有表头结点的非循环双向链表，其每个结点中除有pred(前驱指针)、data (数据)和next (后继指针)域外，还有一个访问频度域freq。在链表被启用前，其值均初始化为零。每当在链表中进行一-次Locate(L,x)运算时，令元素值为x的结点中freq域的值增1,并使此链表中结点保持按访问频度非增(递减)的顺序排列，同时最近访问的结点排在频度相同的结点前面，以便使频繁访问的结点总是靠近表头。试编写符合上述要求的Locate (L,x)运算的算法，该运算为函数过程，返回找到结点的地址，类型为指针型。

代码实现：

//双链表查找元素 再排序
#include<iostream>
using namespace std;
typedef struct lnode{
    int data,f;
    struct lnode *next,*prior;
}lnode,*linklist;
int a[5]={1,2,3,4,5};
int n=5;
void buildlist(linklist &L)
{
    L=(linklist)malloc(sizeof(lnode));
    lnode *r=L,*s;
    L->prior=NULL;
    L->next=L;
    for(int i=0;i<n;i++)
    {
        s=(lnode *)malloc(sizeof(lnode));
        s->data=a[i];
        s->f=0;
        s->next=r->next;
        r->next->prior=s;
        r->next=s;
        s->prior=r;
        r=s;
    }
    r->next=NULL;
}
void disp(linklist L)
{
    lnode *s=L->next;
    while(s)
    {
        cout<<s->data<<" ";
        s=s->next;
    }
    cout<<endl;
}
linklist Locate(linklist &L,int x)
{
    lnode *p=L->next,*q;
    while(p&&p->data!=x) p=p->next;
    if(!p) cout<<"没有x这个结点"<<endl;
    else
    {
        p->f++;
        if(p->next!=NULL) p->next->prior=p->prior;
        p->prior->next=p->next;
        q=p->prior;
        while(q!=L&&q->f<=p->f) q=q->prior;
        p->next=q->next;
        q->next->prior=p;
        p->prior=q;
        q->next=p;
    }
    return p;
}
int main()
{
    linklist L;
    buildlist(L);
    disp(L);
    Locate(L,5);
    Locate(L,5);
    Locate(L,4);
    Locate(L,4);
    disp(L);
    return 0;
}

找到5 

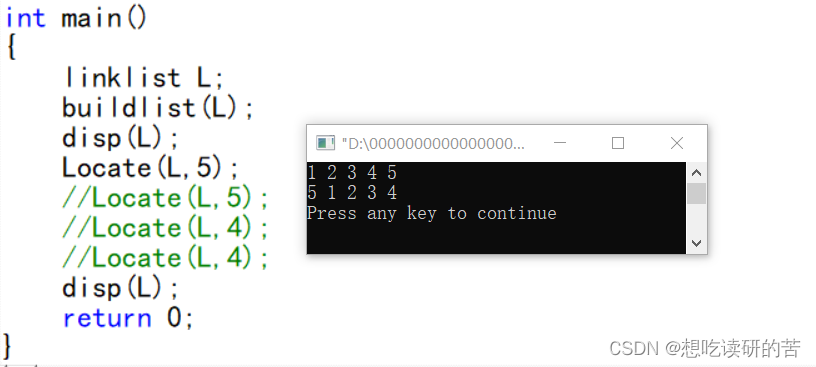
找到5频度2 找到4频度2 选择近的排前

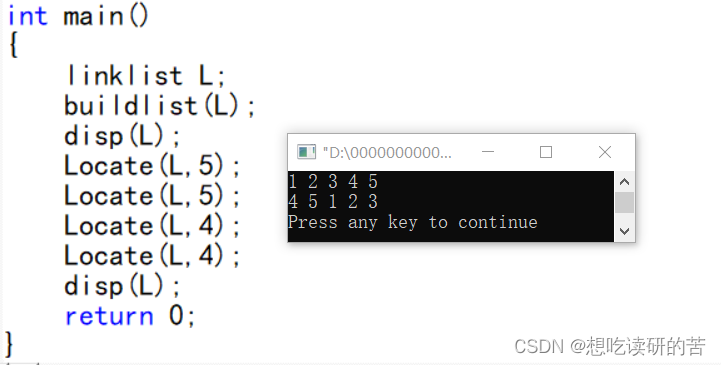
21.单链表有环，是指单链表的最后一个结点的指针指向了链表中的某个结点(通常单链表的最后一个结点的指针域是空的)。试编写算法判断单链表是否存在环。

代码实现：

//判断是否有环 链表
#include<iostream>
using namespace std;
typedef struct lnode{
    int data;
    struct lnode *next;
}lnode;
int a[15]={1,2,3,4,5,6,7,8,9,4,5,6,7,8,9};
int n=15;
void buildlist(lnode *L)
{
    lnode *s,*r=L;
    r->data=a[0];
    for(int i=1;i<n;i++)
    {
        s=(lnode *)malloc(sizeof(lnode));
        s->data=a[i];
        r->next=s;
        r=r->next;
    }
    r->next=NULL;
}
void disp(lnode *L)
{
    lnode *s=L;
    while(s)
    {
        cout<<s->data<<" ";
        s=s->next;
    }
    cout<<endl;
}
lnode* findd(lnode *L)
{
    lnode *f=L,*s=L;
    while(s!=NULL&&f->next!=NULL)
    {
        s=s->next;
        f=f->next->next;
        if(s->data==f->data) break;
    }
    if(s==NULL||f->next==NULL) return NULL;
    lnode *p=L,*q=s;
    while(p->data!=q->data)
    {
        p=p->next;
        q=q->next;
    }
    return p;
}
int main()
{
    lnode list;
    lnode *L=&list;
    buildlist(L);
    cout<<"L:"<<endl;
    disp(L);
    lnode *ans=findd(L);
    cout<<"环口值为:"<<ans->data<<endl;
    return 0;
}

22.已知一个带有表头结点的单链表，结点结构为 data link

假设该链表只给出了头指针list. 在不改变链表的前提下，请设计一个尽可能高效的算法，查找链表中倒数第k个位置上的结点(k为正整数)。若查找成功，算法输出该结点的data域的值，并返回1;否则，只返回0。

代码实现：

//单链表查找倒数第k个结点
#include<iostream>
using namespace std;
typedef struct lnode{
    int data;
    struct lnode *next;
}lnode,*linklist;
int a[5]={5,4,3,10,1};
int n=5;
void buildlist(linklist &L)
{
    L=(linklist)malloc(sizeof(lnode));
    lnode *s,*r=L;
    for(int i=0;i<n;i++)
    {
        s=(lnode *)malloc(sizeof(lnode));
        s->data=a[i];
        r->next=s;
        r=r->next;
    }
    r->next=NULL;
}
int findk(linklist L,int k)
{
    lnode *p=L->next,*q=L->next;
    int num=0;
    while(p!=NULL)
    {
        if(num<k) num++;
        else q=q->next;
        p=p->next;
    }
    if(num<k) return 0;
    else{
        cout<<"倒数第k个结点的值为:"<<q->data<<endl;
        return 1;
    }
} 
int main()
{
    linklist L;
    buildlist(L);
    cout<<findk(L,2)<<endl;
    return 0;
}

找到倒数第k个

没找到倒数第k个

23.假定采用带头结点的单链表保存单词，当两个单词有相同的后缀时，可共享相同的后缀存储空间，例如，"loading" 和"being" 的存储映像如下图所示。

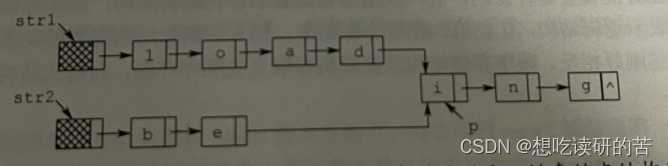
设strl和sr2分别指向两个单词所在单链表的头结点，链表结点结构为data next。请设计一个时间上尽可能高效的算法，找出由str1和str2所指向两个链表共同后的起始位置(如图中字符i所在结点的位置P)。

//公共后缀起始结点
#include<iostream>
using namespace std;
typedef struct lnode{
    char data;
    struct lnode *next;
}lnode,*linklist;
char a[7]={'l','o','a','d','i','n','g'};
char b[5]={'b','e','i','n','g'};
int n1=7,n2=5;
void buildlist(linklist &L,char aa[],int n)
{
    L=(linklist)malloc(sizeof(lnode));
    lnode *s,*r=L;
    for(int i=0;i<n;i++)
    {
        s=(lnode *)malloc(sizeof(lnode));
        s->data=aa[i];
        r->next=s;
        r=r->next;
    }
    r->next=NULL;
}
void disp(linklist L)
{
    lnode *s=L->next;
    while(s)
    {
        cout<<s->data<<" ";
        s=s->next;
    }
    cout<<endl;
}
int length(linklist L)
{
    int ans=0;
    lnode *s=L->next;
    while(s)
    {
        ans++;
        s=s->next;
    }
    return ans;
}
linklist first(linklist L1,linklist L2)
{
    int len1=length(L1),len2=length(L2);
    int dist=abs(len1-len2);
    lnode *p=L1->next,*q=L2->next;
    if(len1>=len2)
    {
        while(dist--)
        {
            p=p->next;
        }
    }
    else
    {
        while(dist--)
        {
            q=q->next;
        }
    }
    while(p)
    {
        if(p->data!=q->data)
        {
            p=p->next;
            q=q->next;
        }
        else return p;
    }
    return p;
}
int main()
{
    linklist L1,L2;
    buildlist(L1,a,n1);
    buildlist(L2,b,n2);
    cout<<"L1:"<<endl;
    disp(L1);
    cout<<"L2:"<<endl;
    disp(L2);
    linklist ans=first(L1,L2);
    cout<<"公共后缀的起始结点为:"<<ans->data<<endl;
    return 0;
}

 24.用单链表保存m个整数，结点的结构为[data][link], 且  I data l < n(n为正整数)。现要求设计一个时间复杂度尽可能高效的算法，对于链表中data的绝对值相等的结点，仅保留第一次出现的结点而删除其余绝对值相等的结点。

代码实现：

//保留链表绝对值相同的首个结点
#include<iostream>
using namespace std;
typedef struct lnode{
    int data;
    struct lnode *next;
}lnode,*linklist;
int a[6]={1,-4,2,3,4,-2};
int n=6;
void buildlist(linklist &L)
{
    L=(linklist)malloc(sizeof(lnode));
    lnode *s,*r=L;
    for(int i=0;i<n;i++)
    {
        s=(lnode *)malloc(sizeof(lnode));
        s->data=a[i];
        r->next=s;
        r=r->next;
    }
    r->next=NULL;
}
void disp(linklist L)
{
    lnode *s=L->next;
    while(s)
    {
        cout<<s->data<<" ";
        s=s->next;
    }
    cout<<endl;
}
void same(linklist &L,int n)
{
    lnode *p=L;
    int *q;
    q=(int *)malloc(sizeof(int)*(n+1));
    for(int i=0;i<n+1;i++) *(q+i)=0;
    int s;
    lnode *f;
    while(p->next!=NULL)
    {
        s=abs(p->next->data);
        if(*(q+s)==0) 
        {
            *(q+s)=1;
            p=p->next;
        }
        else
        {
            f=p->next;
            p->next=f->next;
            free(f);
        }
    }
    free(q);
}
int main()
{
    linklist L;
    buildlist(L);
    cout<<"L"<<endl;
    disp(L);
    same(L,4);
    cout<<"之后"<<endl;
    disp(L);
    return 0;
}

25.设线性表L=(a1,a2,a3,...,an-2,an-1,an)，采用带头节点的单链表保存。设计算法，重新排列L中的节点，得到线性表L'=(a1,an,a2,an-1,a3,an-2,...)。

代码实现：

//链表重组
#include<iostream>
using namespace std;
typedef struct lnode{
    int data;
    struct lnode *next;
}lnode,*linklist;
int a[8]={1,2,3,4,5,6,7,8};
int n=8;
void buildlist(linklist &L)
{
    L=(linklist)malloc(sizeof(lnode));
    lnode *s,*r=L;
    for(int i=0;i<n;i++)
    {
        s=(lnode *)malloc(sizeof(lnode));
        s->data=a[i];
        r->next=s;
        r=r->next;
    }
    r->next=NULL;
}
void disp(linklist L)
{
    lnode *s=L->next;
    while(s)
    {
        cout<<s->data<<" ";
        s=s->next;
    }
    cout<<endl;
}
void newlist(linklist &L)
{
    lnode *p,*q,*l,*r;
    p=L,q=L;
    while(q->next!=NULL)
    {
        p=p->next;
        q=q->next;
        if(q->next!=NULL) q=q->next;
    }
    q=p->next;
    p->next=NULL;
    while(q)
    {
        r=q->next;
        q->next=p->next;
        p->next=q;
        q=r;
    }
    l=L->next;
    q=p->next;
    p->next=NULL;
    while(q)
    {
        r=q->next;
        q->next=l->next;
        l->next=q;
        l=q->next;
        q=r;
    }
}
int main()
{
    linklist L;
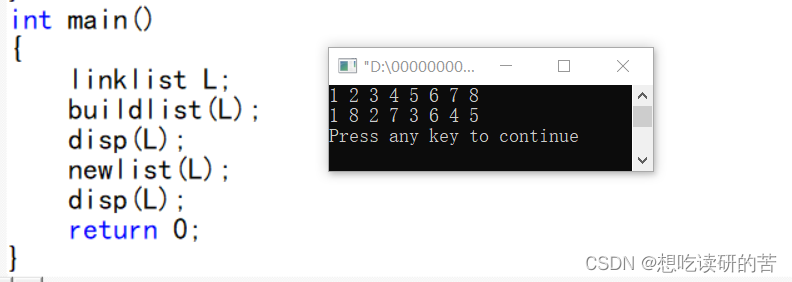
    buildlist(L);
    disp(L);
    newlist(L);
    disp(L);
    return 0;
}