文章目录
第一题: 括号
LeetCode: 面试题 08.09. 括号
描述:
括号。设计一种算法,打印n对括号的所有合法的(例如,开闭一一对应)组合。
说明:解集不能包含重复的子集。
例如,给出 n = 3,生成结果为:
[
“((()))”,
“(()())”,
“(())()”,
“()(())”,
“()()()”
]
解题思路:
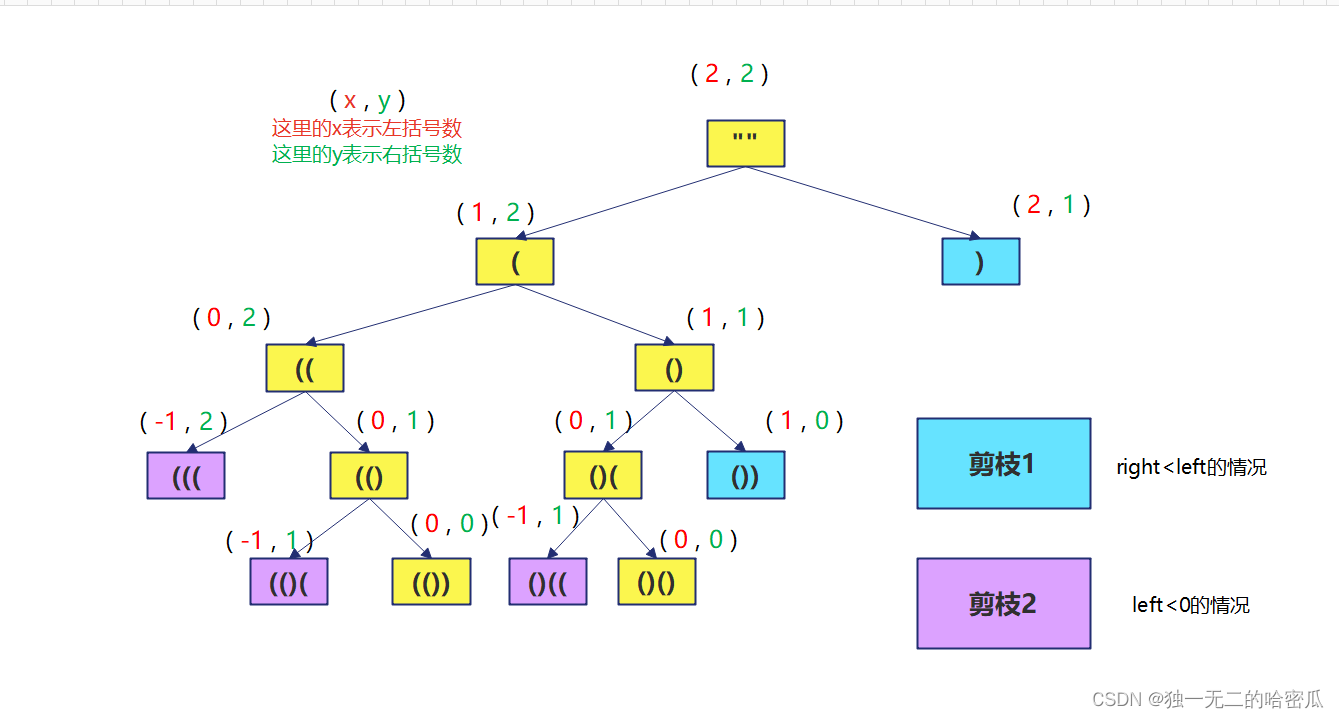
这里使用回溯.
left表示左括号数. right 表示右括号数.
构建字符串, 遇到不合格的就停止, 满足要求就加入list中
注意这里的剪枝,
代码实现:
class Solution {
public List<String> generateParenthesis(int n) {
List<String> res = new ArrayList<>();
backstrack(res,"",n,n);
return res;
}
public void backstrack(List<String> res,String str,int left,int right) {
// 剪枝1 left 或者 right 小于0的情况
if(left < 0 || right < 0) return;
// 剪枝2 left > right的情况
if(left > right) return;
// left和right都为0 此时就满足条件
if(left == 0 && right == 0) {
res.add(str);
return;
}
backstrack(res,str+"(",left-1,right);
backstrack(res,str+")",left,right-1);
}
}
第二题: 硬币
LeetCode: 面试题 08.11. 硬币
描述:
硬币。给定数量不限的硬币,币值为25分、10分、5分和1分,编写代码计算n分有几种表示法。(结果可能会很大,你需要将结果模上1000000007)

解题思路:
动态规划思路:
- 状态 F(i) : 表示当前凑出i的方式
- 状态转移方程: F(i) = (F(i) + F(i-coin)) %1000000007
- 初始状态: F(0) = 1; 因为刚好可以用硬币抽出来.
- 返回结果: F(n)
这里 coins = { 1, 5, 10, 25 };
如果直接遍历, 会有重复的情况, 例如 5 + 10 和 10 + 5
避免这种情况, 就可以使用小循环, 每次小循环只用一种硬币可以避免重复.
代码实现:
class Solution {
public int waysToChange(int n) {
// 当前硬币的情况
int[] coins = {
1,5,10,25};
int[] dp = new int[n+1];
// 例如 dp[1] = dp[1] + dp[0], 这里就表示刚好可以使用当前硬币,初始化就为1
dp[0] = 1;
// 外层遍历这个coins数组
for(int coin : coins) {
// 内层 遍历一种硬币
for(int i = coin;i <= n; i++) {
dp[i] = (dp[i] + dp[i-coin]) % 1000000007;
}
}
return dp[n];
}
}
第三题: 变位词组
LeetCode: 面试题 10.02. 变位词组
描述:
编写一种方法,对字符串数组进行排序,将所有变位词组合在一起。变位词是指字母相同,但排列不同的字符串。

解题思路:
- 遍历, 让遍历到的字符串进行排序, 添加到HashMap中key为排序后的字符串, value为一个list
- 把排序后的字符相同的,加入到同一个list中
- 不同的就新添加一个list.
- 遍历结束之后, 把所有的list添加到一起
代码实现:
class Solution {
public List<List<String>> groupAnagrams(String[] strs) {
List<List<String>> list = new ArrayList<>();
Map<String,List<String>> map = new HashMap<>();
for(String str : strs) {
// 进行排序
char[] ch = str.toCharArray();
Arrays.sort(ch);
// 排序后的字符数组变成字符串
String s = new String(ch);
if(!map.containsKey(s)) {
//这里是不存在相同key的情况, 需要创建一个新的list
List<String> ret = new ArrayList<>();
ret.add(str);
map.put(s,ret);
}else{
//这里是存在相同的key的情况, 需要得到之前的list,然后添加数据
map.get(s).add(str);
}
}
// 使用keySet的方法得到key, 然后把所有的value值添加到一起.
for(String key : map.keySet()) {
list.add(map.get(key));
}
return list;
}
}
第四题: 最小差
LeetCode: 面试题 16.06. 最小差
描述:
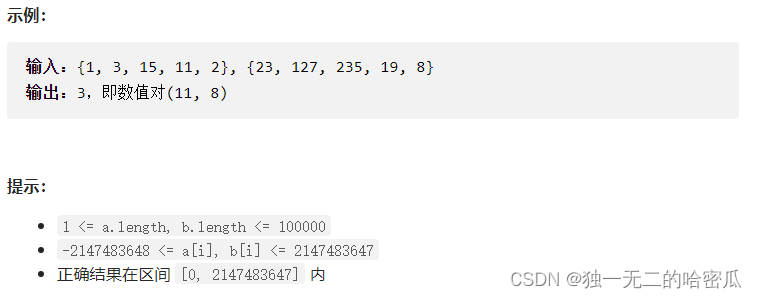
给定两个整数数组a和b,计算具有最小差绝对值的一对数值(每个数组中取一个值),并返回该对数值的差
解题思路:
- 定义两个指针, left right, 对两个数组进行排序.
- 用 ret 记录当前 a[left] - b[right] 的差值
如果ret > 0, a[left]>b[right], 就让right++, 为了让b的值更接近a的值
如果ret < 0, a[left]<b[right], 就让left++, 为了让a的值更接近b的值
记录 最小的ret
代码实现:
class Solution {
public int smallestDifference(int[] a, int[] b) {
// 先排序
Arrays.sort(a);
Arrays.sort(b);
// 注意这里的溢出
long min = Integer.MAX_VALUE;
int left = 0;
int right = 0;
while(left < a.length && right < b.length) {
// long 防止溢出
long ret = a[left] - b[right];
// 记录最小值
min = Math.min(Math.abs(ret),min);
// 让更接近的值相减
if(ret < 0) left++;
else right++;
}
return (int)min;
}
}
第五题: 首个共同祖先
LeetCode: 面试题 04.08. 首个共同祖先
描述:
设计并实现一个算法,找出二叉树中某两个节点的第一个共同祖先。不得将其他的节点存储在另外的数据结构中。注意:这不一定是二叉搜索树。
例如,给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]

解题思路:
- 可能出现的情况:
①p 和 q有一个为根节点, 那么该根节点就是最近公共祖先
②p 和 q不在同一颗子树下, 那么他们的父亲就是公共祖先
③p 和 q在同一颗子树下- 递归左右子树
① 左右子树都不为空, 那么root就是公共祖先
② 左子树为空, 右子树不为空, 那么右树找到的节点就是公共祖先
③ 左子树不为空, 右子树为空, 那么左树找到的节点就是公共祖先
代码实现:
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
// 情况一: 根节点为空
if (root == null) return null;
// 情况二: p或q为根节点
if (p == root || q == root) return root;
// 遍历左右子树
TreeNode leftNode = lowestCommonAncestor(root.left,p,q);
TreeNode rightNode = lowestCommonAncestor(root.right,p,q);
// 都不为空, 那么root就是公共祖先
if(leftNode != null && rightNode != null) {
return root;
}
// 左子树为空, 右树的节点就是公共祖先
if(leftNode == null){
return rightNode;
}
// 右子树为空, 左树的节点就是公共祖先
if(rightNode == null) {
return leftNode;
}
return null;
}
}
第六题: 最小高度树
LeetCode: 面试题 04.02. 最小高度树
描述:
给定一个有序整数数组,元素各不相同且按升序排列,编写一个算法,创建一棵高度最小的二叉搜索树。

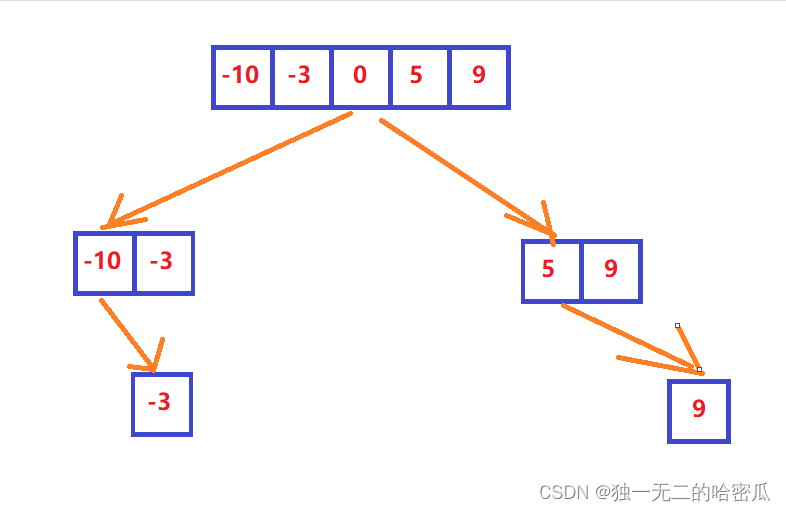
解题思路:
- 这里就使用二分方法来分割, 每次取得中间点, 然后构造一个节点.
- 然后在左边取得一个中间点, 构造左节点, 再右边取得一个中间点, 构造右节点.
代码实现:
class Solution {
public TreeNode sortedArrayToBST(int[] nums) {
return makeBST(nums,0,nums.length-1);
}
public TreeNode makeBST(int[] nums, int left, int right) {
// 如果left>right就不合法了
if (left > right) {
return null;
}
// 这里防止溢出, 使用left+(right-left)/2
int mid = left + (right - left) / 2;
// 构造一个节点
TreeNode node = new TreeNode(nums[mid]);
// 构造左右子树
node.left = makeBST(nums, left, mid - 1);
node.right = makeBST(nums, mid+1, right);
return node;
}
}