一维非齐次热传导方程的向后 Euler 格式
考虑如下热方程:
{ ∂ u ∂ t = ∂ 2 u ∂ x 2 , 0 ≤ x ≤ 1 , 0 ≤ t ≤ 1 u ( x , 0 ) = e x , 0 ≤ x ≤ 1 u ( 0 , t ) = e t , u ( 1 , t ) = e 1 + t , , 0 ≤ t ≤ 1 \begin{cases}\frac{\partial u}{\partial t}=\frac{\partial^{2} u}{\partial x^{2}} & , 0 \leq x \leq 1,0 \leq t \leq 1 \\ u(x, 0)=e^{x} & , 0 \leq x \leq 1 \\ u(0, t)=e^{t}, u(1, t)=e^{1+t}, & , 0 \leq t \leq 1\end{cases} ⎩⎪⎨⎪⎧∂t∂u=∂x2∂2uu(x,0)=exu(0,t)=et,u(1,t)=e1+t,,0≤x≤1,0≤t≤1,0≤x≤1,0≤t≤1
该问题的精确解为 u ( x , t ) = e x + t u(x, t)=e^{x+t} u(x,t)=ex+t.
差分格式
定义误差为
E ∞ ( h , τ ) = max 1 ≤ i ≤ m − 1 1 ≤ k ≤ n ∣ u ( x i , t k ) − u k k ∣ E_{\infty}(h, \tau)=\max _{1 \leq i \leq m-1 \atop 1 \leq k \leq n} \mid u\left(x_{i}, t_{k}\right)-u_{k}^{k} \mid E∞(h,τ)=1≤k≤n1≤i≤m−1max∣u(xi,tk)−ukk∣
用向后 Euler 格式求下述问题的数值解并对数值解、精度和误差阶进行相应的数值分析.
解:
将 x x x 进行 m m m 等分, 将 t t t 进行 n n n 等分, 记 h = 1 m , τ = 1 n h=\frac{1}{m}, \tau=\frac{1}{n} h=m1,τ=n1
x i = i h , 0 ≤ i ≤ m t k = k τ , 0 ≤ k ≤ n \begin{aligned} &x_{i}=i h, 0 \leq i \leq m \\ &t_{k}=k \tau, 0 \leq k \leq n \end{aligned} xi=ih,0≤i≤mtk=kτ,0≤k≤n
向后 Euler 差分格式为
{ − γ u i − 1 k + ( 1 + 2 γ ) u i k − γ u i + 1 k = u i k − 1 + τ f ( x i , t k ) u i 0 = e x i u 0 k = e t k , u m k = e 1 + t k \left\{\begin{array}{l} -\gamma u_{i-1}^{k}+(1+2 \gamma) u_{i}^{k}-\gamma u_{i+1}^{k}=u_{i}^{k-1}+\tau f\left(x_{i}, t_{k}\right) \\ u_{i}^{0}=e^{x_{i}} \\ u_{0}^{k}=e^{t_{k}}, u_{m}^{k}=e^{1+t_{k}} \end{array}\right. ⎩⎨⎧−γui−1k+(1+2γ)uik−γui+1k=uik−1+τf(xi,tk)ui0=exiu0k=etk,umk=e1+tk
其中, 1 ≤ i ≤ m − 1 , 1 ≤ k ≤ n , γ = τ h 2 1 \leq i \leq m-1,1 \leq k \leq n, \gamma=\frac{\tau}{h^{2}} 1≤i≤m−1,1≤k≤n,γ=h2τ
f ( x i , t k ) = 0 f\left(x_{i}, t_{k}\right)=0 f(xi,tk)=0
写成矩阵形式 A u = f A u=f Au=f
其中
A = [ 1 + 2 γ − γ − γ 1 + 2 γ − γ 2 ⋱ ⋱ ⋱ − γ 1 + 2 γ ] u k = [ u 1 k , u 2 k , ⋯ , u m − 1 k ] T \begin{gathered} A=\left[\begin{array}{cccc} 1+2 \gamma & -\gamma & & \\ -\gamma & 1+2 \gamma & -\frac{\gamma}{2} & \\ & \ddots & \ddots & \ddots \\ & & -\gamma & 1+2 \gamma \end{array}\right] \\ u^{k}=\left[u_{1}^{k}, u_{2}^{k}, \cdots, u_{m-1}^{k}\right]^{T} \end{gathered} A=⎣⎢⎢⎡1+2γ−γ−γ1+2γ⋱−2γ⋱−γ⋱1+2γ⎦⎥⎥⎤uk=[u1k,u2k,⋯,um−1k]T
f = [ u 1 k − 1 + γ u 0 k , u 2 k − 1 , ⋯ , u m − 2 k − 1 , u m − 1 k − 1 + γ u m k ] T f=\left[u_{1}^{k-1}+\gamma u_{0}^{k}, u_{2}^{k-1}, \cdots, u_{m-2}^{k-1}, u_{m-1}^{k-1}+\gamma u_{m}^{k}\right]^{T} f=[u1k−1+γu0k,u2k−1,⋯,um−2k−1,um−1k−1+γumk]T
数值结果
解方程, 由第 k \mathrm{k} k 层的值, 能够求出第 k + 1 \mathrm{k}+1 k+1 层的值。
解题程序运行于 Matlab 2018a.
当 τ = 1 100 , h = 1 10 \tau=\frac{1}{100}, h=\frac{1}{10} τ=1001,h=101 时, t = 1 \mathrm{t}=1 t=1 处的数值解和精确解见下图, 从图像上看很接近。
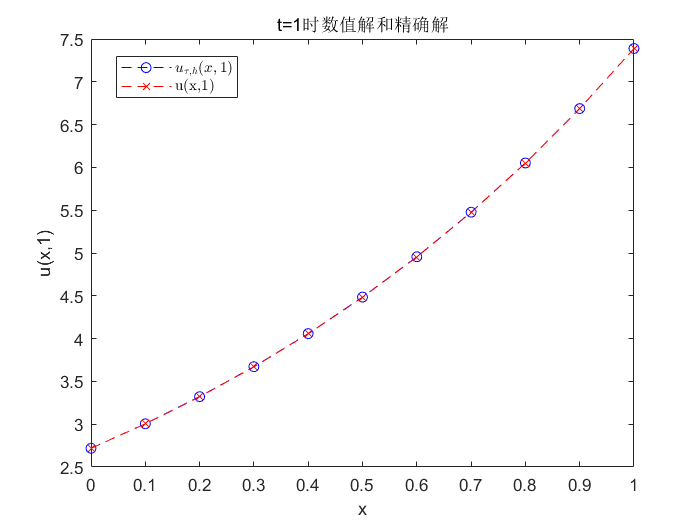
当 τ = 1 100 , h = 1 10 \tau=\frac{1}{100}, h=\frac{1}{10} τ=1001,h=101 时, 取 x = 0.5 \mathrm{x}=0.5 x=0.5, 不同 t \mathrm{t} t 处的值见表 1 , 当层数越深时, 误差越大, 这是因为, 每一次由 k \mathrm{k} k 层求解 k + 1 \mathrm{k}+1 k+1 层时都有误差, 随着 t \mathrm{t} t 的增大, 误差不断累积, 越来越大, 到 t = 1 \mathrm{t}=1 t=1 处误差变得最大。
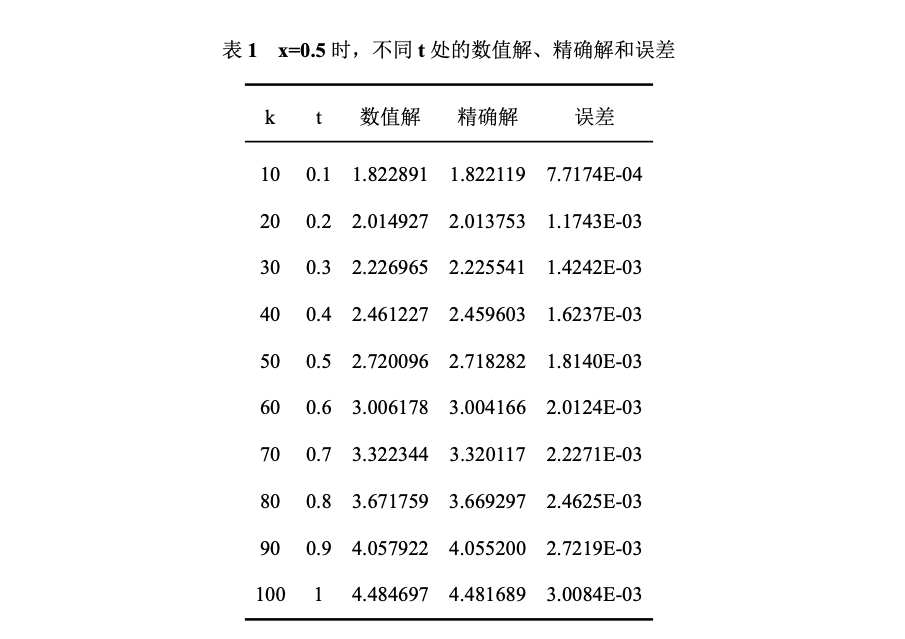
取不同 τ \tau τ 和 h h h 时, t = 1 \mathrm{t}=1 t=1 处的误差见图 2 , 步长越小, 误差也越小。
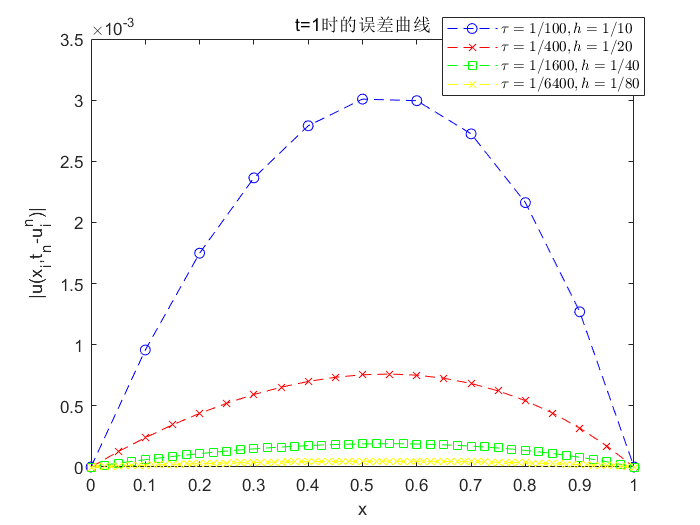
取不同步长时, 误差和误差比见图用向后 Euler 格式, τ \tau τ 变为原来的 4 倍, h h h 变为原 来的 2 倍, 误差会变为原来的 4 倍, 符合 O ( τ + h 2 ) O\left(\tau+h^{2}\right) O(τ+h2) 的截断误差
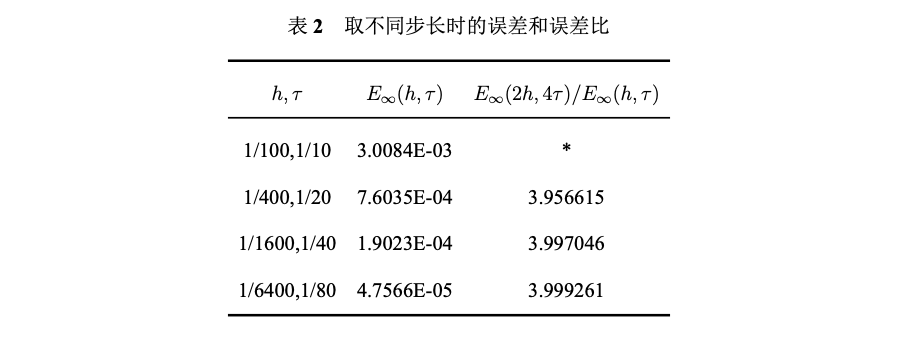
源代码
说明文档:
fa.m求精确解
fsolve.m用Euler向后格式求数值解
fig.m绘制误差图,精确解和数值解对比图
data.m求特定点的数值解,误差分析。
fsolve.m
function [t,x,u] = fsolve(tau,h)
% 用向后Euler法解抛物方程
% @t 时间向量
% @x 空间向量
% @tau 时间步长
% @h 空间步长
% @u 数值解
N=1/tau;%t被分割的区间数
M=1/h;%x被分割的区间数
t=0:tau:1;
x=0:h:1;
u=ones(N+1,M+1);
u(1,:)=exp(x);%初值
%边值
u(:,1)=exp(t);
u(:,M+1)=exp(1+t);
r=tau/h^2;%步长系数
a=ones(M-2,1)*(-r);%下对角线
c=ones(M-2,1)*(-r);%上对角线
b=ones(M-1,1)*(1+2*r);%主队角线
A=diag(b,0)+diag(a,-1)+diag(c,1);%系数矩阵
for k=2:N+1
%右端项
f=u(k-1,2:M);
f(1)=f(1)+r*u(k,1);
f(M-1)=f(M-1)+r*u(k,M+1);
u(k,2:M)=(A\f')';%由k-1层求第k层的值
end
end
data.m
clc;clear;
tao=[1/100,1/400,1/1600,1/6400];%时间步长
h=[1/10,1/20,1/40,1/80];%空间步长
K=size(tao,2);
t_cell=cell(K,1);%时间向量
x_cell=cell(K,1);%空间向量
u_cell=cell(K,1);%数值解
ua_cell=cell(K,1);%精确解
epsilon_cell=cell(K,1);%绝对误差
max_epsilon=ones(K,1);
rate=ones(3,1);%误差比
for n=1:K
[t_cell{n,1},x_cell{n,1},u_cell{n,1}]=fsolve(tao(n),h(n));%求数值解
ua_cell{n,1}=fa(t_cell{n,1},x_cell{n,1});%精确解
epsilon_cell{n,1}=abs(ua_cell{n,1}-u_cell{n,1});%求绝对误差
max_epsilon(n,1)=max(epsilon_cell{n,1}(:));%求最大误差
end
%E(t,h)/E(4t,2h)
for n=1:K-1
rate(n,1)=max_epsilon(n,1)/max_epsilon(n+1,1);
end
%当x=0.5时,取t=0.1,0.2,...1时,误差的变化,tao=1/100,h=1/10;
u_1=ones(10,1);%特定点数值解
ua_1=ones(10,1);%特定点精确解
[t,x,u]=fsolve(tao(1),h(1));
ua=fa(t,x);
u_1=u(11:10:101,6);
ua_1=ua(11:10:101,6);
epsion_1=abs(u_1-ua_1);%误差
fa.m
function r =fa(t,x)
% 求精确解
% @t 时间向量
% @x 空间向量
[t,x]=meshgrid(t,x);
t=t';
x=x';
r=exp(x+t);
end
fig.m
clc;clear;
tau=[1/100,1/400,1/1600,1/6400];%时间步长
h=[1/10,1/20,1/40,1/80];%空间步长
K=size(tau,2);
t_cell=cell(K,1);%时间向量
x_cell=cell(K,1);%空间向量
u_cell=cell(K,1);%数值解
ua_cell=cell(K,1);%精确解
epsilon_cell=cell(K,1);%绝对误差
for n=1:K
[t_cell{n,1},x_cell{n,1},u_cell{n,1}]=fsolve(tau(n),h(n));%求数值解
ua_cell{n,1}=fa(t_cell{n,1},x_cell{n,1});%精确解
epsilon_cell{n,1}=abs(ua_cell{n,1}-u_cell{n,1});%求绝对误差
end
figure(1);
%t=1,tau=1/100,h=1/10时数值解和精确解对比
plot(x_cell{1,1},u_cell{1,1}(1/tau(1)+1,:),'b--o'...
,x_cell{1,1},ua_cell{1,1}(1/tau(1)+1,:),'r--x')
h=legend('$u_{\tau,h}(x,1)$','u(x,1)');
set(h,'Interpreter','latex') %设置legend为latex解释器
title('t=1时数值解和精确解');
xlabel('x');ylabel('u(x,1)');
%绘制t=1时的误差曲线
figure(2)
plot(x_cell{1,1},epsilon_cell{1,1}(1/tau(1)+1,:),'b--o');
hold on;
plot(x_cell{2,1},epsilon_cell{2,1}(1/tau(2)+1,:),'r--x');
hold on;
plot(x_cell{3,1},epsilon_cell{3,1}(1/tau(3)+1,:),'g--s');
hold on;
plot(x_cell{4,1},epsilon_cell{4,1}(1/tau(4)+1,:),'y--x');
hold on;
h=legend('$\tau=1/100,h=1/10$','$\tau=1/400,h=1/20$','$\tau=1/1600,h=1/40$','$\tau=1/6400,h=1/80$');
set(h,'Interpreter','latex') %设置legend为latex解释器
title('t=1时的误差曲线');
xlabel('x');ylabel('|u(x_{i},t_{n}-u_{i}^{n})|');