超出时间限制:
1)死循环
2)递归的次数太多了
1.获取到二叉树中的结点的个数
这个题可以具体分为遍历思路和子问题思路
遍历思路:我们可以自己定义一个计数器(计数器是不可以变成局部变量的),int count=0;遍历二叉树,如果他是节点,我们就让计数器++即可;直到把这棵二叉树遍历完成;
那么怎样判断它是否为节点呢?只要他的root不为空,那么就说明他是节点
public int preprint(Node root) {
if (root == null) {
return 0;
}
count++;
System.out.println(root.data);
preprint(root.left);
preprint(root.right);
return count;
}子问题思路:一个二叉树总共的节点个数=root的左孩子的结点点个数+root的右孩子结点个数+1;
public int getCount(Node root)
{
if(root==null)
{
return 0;
}
return getCount(root.left)+getCount(root.right)+1;
} A
B C
D E F G
H我们以这个二叉树举例来说,我们调用了A的getCount(root.left)+getCount(root.right)+1,我们在这个部分必须执行完A的左边部分的getCount部分,才可以执行右边
1)在调用A的getCount(root.left)的时候,我们传的参数是B
2)再次调用B的getCount(root.left)+get(root.right)+1,在B的getCount函数左边,我们又调用了D的getCount函数
3)我们调用D的getCount(root.left)+getCount(root.right)+1函数,最后一次调用的时候,先调用左边,传过去的参数为空,返回0,在调用D的第二个函数,传过去的参数也是空,返回0,所以说D的整个函数的调用结束了,返回1
4)这时B的左边的getCount(D)已经执行完了,况且返回值是1,继续执行右边
5)前三次进行调用的时候,A,B,D的右边函数都是没有被执行到的,直至D返回了,才依次执行;
2.获取到叶子结点的个数
遍历思路来进行解决:遍历到叶子节点,我就让计数器++,如何判断是叶子节点?他的左树和右树都是空
子问题思路来进行解决: 左树的叶子节点+右树的叶子节点
遍历思路的代码:我们遍历整个二叉树的所有结点(前序遍历,中序遍历,层序遍历都可以),如果说我们遍历到了一个节点,发现它的左子树是空况且他的右子树也是空,那么我们就要用引用计数++
public int preprint(Node root) {
if (root == null) {
return 0;
}
if(root.left==null&&root.right==null)
{
count++;
}
preprint(root.left);
preprint(root.right);
return count;
}
子问题思路的代码:此时我们假设只有一个节点,只有一个根root节点,如果它的左子树为空,况且它的右子树为空,那么就直接返回个1即可;

如果有很多个节点,直接返回左子树的叶子节点和右子树的叶子节点相加之和即可;
preroot(root.left)+preroot(root.right),一直向下执行,况且在向下的过程中始终无法执行root.right的代码,只有说下一个的root.left和root.right全部执行完了才可以执行上面的root.right
public int preprint(Node root) {
if (root == null) {
return 0;
}
if(root.left==null&&root.right==null)
{
return 1;
}
return preprint(root.left)+preprint(root.right);
}3.获取第k层结点的个数(先想一想只有一个节点,k=1)
子问题思路:要求这棵树的第K层节点,实质上是求左树的第K-1层的结点,和右树的第K-1层的结点,然后进行相加即可;
int getLevelNodecount(Node root,int k) { if(root==null||k<=0) { return 0; } if(k==1) { return 1; } return getLevelNodecount(root.left,k-1)+getLevelNodecount(root.right,k-1); }
4.获取二叉树的高度(获取到二叉树的高度,先求左树的高度,再进行求解有右树的高度,比较他们俩谁大,就是整棵树的高度)(先想一想只有一个节点,没有节点,高度是多少)
二叉树的高度本质上就是深度
子问题思路:就是左树的高度和右树的高度取最大值,加1即可=整棵树的高度
如果传过来的root为空,那么高度就是0,如果它的左子树和他的右子树都不为空,那么直接返回1即可;
然后再直接调用函数求左子树的高度和右子树的高度,然后返回他们的最大值+1即可
public int maxDepth(TreeNode root) {
if(root==null)
{
return 0;
}
if(root.left==null&&root.right==null)
{
return 1;
}
int left=maxDepth(root.left);//求出左树的高度
int right=maxDepth(root.right);//求出右树的高度
return left>right?left+1:right+1;
每一层递归,都是执行一次
递归次数=每一个节点都要遍历一次O(N)
空间复杂度logN=高度
5.检测值为value的数值是否存在(先想一想只有一个节点,只有三个节点的完全二叉树)
做题思路:
我们现在假设在数组当中查找一个数据,遍历数组,依次进行查找
假设现在是在链表当中,也是需要从头节点开始进行比较,看是不是我们要查询的节点
现在是放在了二叉树里面,先遍历二叉树的节点
先进行判断根结点的值是不是你要进行查找的值,如果不是先去左边找,还不是,就从右边去找
public Node Search(Node root,int Value)
{
if(root==null)
{
return null;
}
if(root.data==Value)
{
return root;
}
Node node=Search(root.left,Value);//先到左树去查找Value的值
if(node!=null)
{
return node;
}
node=Search(root.right,Value);//再去右树去查找Value的值,无论查到查不到最终一定会返回一个值,不为空就进行返回
if(node!=null)
{
return node;
}
return null;
}5.判断一棵树是否是完全二叉树
我们在这里面需要使用一个数据结构,叫做队列,我们遍历这棵二叉树,只要这个节点,我们就把他入队列;
再进行出队列,如果出队列的这个节点不是空,把他的左孩子和右孩子都放到队列里面(出来的这个节点的左右孩子为空也进行入队列)
boolean IsCompleteTree(Node root)
{
if(root==null)
{
return false;
}
Queue<Node> queue=new LinkedList<>();
queue.offer(root);
while(!queue.isEmpty())
{
Node node=queue.poll();
if(node!=null)
{
queue.offer(node.left);
queue.offer(node.right);
}else {
break;
}
}
while(!queue.isEmpty())
{
Node node1=queue.poll();
if(node1!=null)
{
return false;
}
}
return true;
}
6.二叉树的最近的公共祖先(二叉搜索树中序遍历是有序的)
学会和面试官一起讨论问题
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
例如,给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]
示例 1:
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出: 3
解释: 节点 5 和节点 1 的最近公共祖先是节点 3。
示例 2:
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出: 5
解释: 节点 5 和节点 4 的最近公共祖先是节点 5。因为根据定义最近公共祖先节点可以为节点本身。
说明:
所有节点的值都是唯一的。
p、q 为不同节点且均存在于给定的二叉树中。
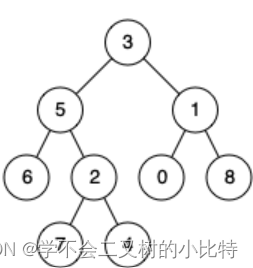
比如说6和8的最近公共祖先是3
思路1:假设现在这棵树是一棵二叉搜索树:
1)如果它的根节点是P或者根节点是Q,那么他们的公共祖先就是root
2)如果它的root为空,那么根本就扯不上最近公共祖先
3)如果说p.data<root.data&&q.data>root.data那么p在根节点的左子树上面,q在根节点的右子树上面;公共节点就是root;
4)如果说p.data>root.data&&q.data<root.data那么p在根节点的右子树上面,q在根节点的左子树上面;公共节点就是root;
5)如果说p.data<root.data&&q.data<root.data那么p和q都在根节点的左边,直接递归左树,如果说p在q的上面,直接先遍历到p就进行返回(此时发现新的递归的root为p);
6)如果说p.data>root.data&&q.data>root.val那么p和q都在根节点的右边,直接递归右树,如果p在q的上面,那么直接返回p;
对于遍历左树和遍历右树来说,找节点都是在同一层进行查找的;分别在两边查找的时候,例如在左边查找,遇到p或者q只返回一个;
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root==null)
{
return null;
}
if(p==root||q==root)
{
return root;
}
//我们查找都是针对同一层进行查找,先找下一层看看有没有root等于p或者q的
TreeNode s1=lowestCommonAncestor(root.left,p,q);
TreeNode s2=lowestCommonAncestor(root.right,p,q);
if(s1!=null&&s2!=null)//在左边和右边都找到了
{
return root;
}else if(s1!=null&&s2==null)//左边找到了,右边没有找到
{
return s1;
}else{//右边找到了,左边没有找到
return s2;
}
思路2:假设这棵二叉树是以孩子双亲表示法进行表示的,一个结点里面有四个域,data,left,right,parent;这个问题就转化成了两个链表求交点;
先从根节点进行遍历,一直到P结点,求出长度,整合成一条链表;
我们再从根节点进行遍历,一直到Q结点,求出长度,整合成一张链表;
我们在以P,Q分别为头节点,先让链表短的那一方先走差值步,尾巴节点都是root,再分别一人走一步(parent=node.parent)直到相交进行返回即可
1)但是实际上很遗憾,他们并不是双亲结点(孩子节点表示法进行表示的)
2)我们是用两个栈来分别进行存储P的路径和Q的路径,求两个栈的大小,先让长度较大的那个栈先出差值步;
3)让元素较多的那个栈走差值步之后(出差值个元素),我们同时让两个栈出元素,直到两个栈出的结点是相同的
但是在这个过程中我觉得最难的部分就是如何用两个栈来存储对应的节点的路径呢?也就是说咱们如何找到从根节点到指定的结点的路径把它们放到栈里面去呢?
在这个过程我们写一个函数,要遍历原来的二叉树
我们可以假设只有三个节点,我们是一定要存放根节点的,如果root.data!=node.data,那么就像root.left去找node结点,找到了就返回true;如果没有找到,就去root.right去找,找到了就返回true;代码走到最后一步,说明在以这个节点为根节点的左右子树都无法找到这个结点,那么就肯定是找不到了,直接弹出栈顶元素即可
root:整个二叉树的根节点
node:我们所指定的节点
stack:保存从根节点到这个所指定的节点的路径
public boolean GetPath(TreeNode root, TreeNode node, Stack<TreeNode> stack)
{
if(root==null||node==null)
{
return false;
}
stack.push(root);//我们是一定要把根节点存放在栈里面的
if(root==node)
{
return true;
}
Boolean flag1=GetPath(root.left,node,stack);
if(flag1==true)
{
return true;
}
Boolean flag2=GetPath(root.right,node,stack);
if(flag2==true)
{
return true;
}
stack.pop();
return false;
}
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root==null) return null;
Stack<TreeNode> stackp=new Stack<>();
Stack<TreeNode> stackq=new Stack<>();
GetPath(root,p,stackp);
GetPath(root,q,stackq);
int count1=stackp.size();
int count2=stackq.size();
if(count1>count2)
{
for(int i=0;i<count1-count2;i++)
{
stackp.pop();
}
}else{
for(int j=0;j<count2-count1;j++)
{
stackq.pop();
}
}
while(!stackp.empty()&&!stackq.empty())
{
if(stackp.peek()==stackq.peek())
{
return stackq.pop();
}else{
stackq.pop();
stackp.pop();
}
}
return null;
}