文章是观看王争老师的数据结构与算法之美所写
前言
本文将会讲解以下内容
- 最好情况时间复杂度
- 最坏情况时间复杂度
- 平均情况时间复杂度
- 均摊时间复杂度
最好、最坏情况时间复杂度
// n表示数组array的长度
int find(int[] array, int n, int x) {
int i = 0;
int pos = -1;
for (; i < n; ++i) {
if (array[i] == x) {
pos = i;
break;
}
}
return pos;
}
我们先来看看上面这个代码的时间复杂度
- 如果情况好的话,我们可能第一个元素就找到了,就不需要遍历剩余元素,时间复杂度就是O(1)
- 如果情况很糟糕的话,可能找不到此元素,我们需要遍历数组所有元素,时间复杂度为O(n)。
- 在不同的情况下,这段代码的时间复杂度是不一样的。
为了表示代码在不同情况下的不同时间复杂度,我们需要引入三个概念:最好情况时间复杂度、最坏情况时间复杂度和平均情况时间复杂度。
平均情况时间复杂度
要查找的变量 x 在数组中的位置,有 n+1 种情况:在数组的 0~n-1 位置中和不在数组中。我们把每种情况下,查找需要遍历的元素个数累加起来,然后再除以 n+1,就可以得到需要遍历的元素个数的平均值,即:
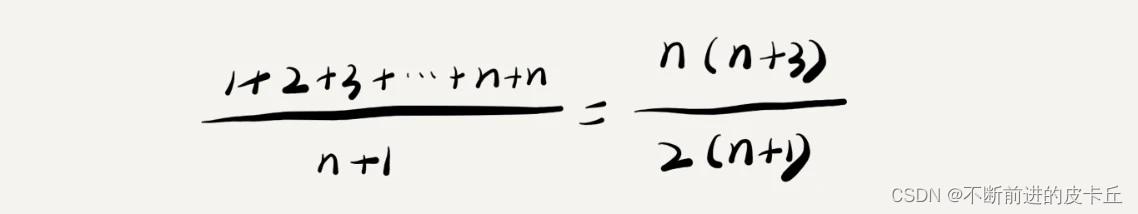
在时间复杂度的大O表达法中,我们可以得到时间复杂度是O(n),但是这样计算的话,计算过程是有问题的,也是我们容易犯错的地方
我们知道,要查找的变量 x,要么在数组里,要么就不在数组里。我们假设在数组中与不在数组中的概率都为 1/2。另外,要查找的数据出现在 0~n-1 这 n 个位置的概率也是一样的,为 1/n。所以,根据概率乘法法则,要查找的数据出现在 0~n-1 中任意位置的概率就是 1/(2n)。
那么,平均时间复杂度就是: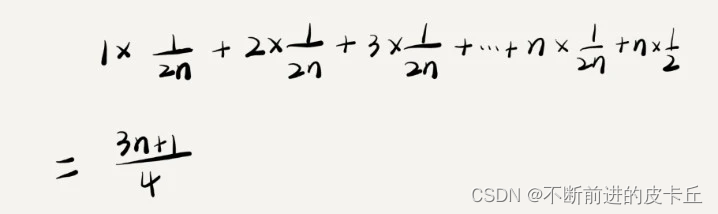
这个值就是概率论中的加权平均值,也叫作期望值,所以平均时间复杂度的全称应该叫加权平均时间复杂度或者期望时间复杂度。
用大O表示法仍然是O(n)