基于自适应头狼的灰狼优化算法
摘要: 灰狼优化算法一种模拟灰狼捕食行为的元启发式优化算法. 由于灰狼算法在种群迭代更新中始终靠近最优解,所以易陷入局部最优. 提出了一种基于自适应头狼的灰狼优化算法,并在个体迭代更新中选择合适的头狼个数进行个体更新,这使得算法能够平衡开发和勘探能力.
1.灰狼优化算法
基础灰狼算法的具体原理参考,我的博客:https://blog.csdn.net/u011835903/article/details/107716390
2.自适应头狼的灰狼优化算法(AL-GWO)
在 GWO 中,头狼的个数设置为 3,理论上讲,头狼的个数影响着算法的开发和勘探能力.因此,本研究对 GWO 进行改进的方法是在更新个体的过程中随机选择头狼的个数. 而对于迭代过程中开发和勘探能力的区分是通过如下的 A’来完成的.
A ′ = 2 a ⋅ r 1 − a (8) A^{\prime}=2 a \cdot r_{1}-a \tag{8} A′=2a⋅r1−a(8)
由式(8)可知,A’是区间[-a,a]中的一个随机值,其中 a 在迭代过程中从 2 减少到 0.
若增加头狼的数量,即由狼α 引导狼 β、狼 δ 和狼 γ 来进行猎物攻击. 狼 α、狼 β、狼 δ 和狼 γ 用到目前为止已获得的 4 个最优解来表示,更新公式为:
D α = ∣ C 1 ⋅ X α − X ∣ , D β = ∣ C 2 ⋅ X β − X ∣ , D δ = ∣ C 3 ⋅ X δ − X ∣ , D γ = ∣ C 4 ⋅ X γ − X ∣ X 1 = X α − A 1 ⋅ D α , X 2 = X β − A 2 ⋅ D β , X 3 = X δ − A 3 ⋅ D δ , X 4 = X γ − A 4 ⋅ D γ X ( t + 1 ) = X 1 + X 2 + X 3 + X 4 4 \begin{array}{l} \mathrm{D}_{\alpha}=\left|\boldsymbol{C}_{1} \cdot X_{\alpha}-X\right|, D_{\beta}=\left|\boldsymbol{C}_{2} \cdot X_{\beta}-X\right|, \\ D_{\delta}=\left|\boldsymbol{C}_{3} \cdot X_{\delta}-X\right|, D_{\gamma}=\left|\boldsymbol{C}_{4} \cdot X_{\gamma}-X\right| \\ X_{1}=X_{\alpha}-A_{1} \cdot D_{\alpha}, X_{2}=X_{\beta}-A_{2} \cdot D_{\beta}, \\ X_{3}=X_{\delta}-A_{3} \cdot D_{\delta}, X_{4}=X_{\gamma}-A_{4} \cdot D_{\gamma} \\ X(t+1)=\frac{X_{1}+X_{2}+X_{3}+X_{4}}{4} \end{array} Dα=∣C1⋅Xα−X∣,Dβ=∣C2⋅Xβ−X∣,Dδ=∣C3⋅Xδ−X∣,Dγ=∣C4⋅Xγ−X∣X1=Xα−A1⋅Dα,X2=Xβ−A2⋅Dβ,X3=Xδ−A3⋅Dδ,X4=Xγ−A4⋅DγX(t+1)=4X1+X2+X3+X4
同样,若减小头狼数量,即由狼 α 引导狼 β来进行猎物攻击,则更新公式为,
D α = ∣ C 1 ⋅ X α − X ∣ , D β = ∣ C 2 ⋅ X β − X ∣ X 1 = X α − A 1 ⋅ D α , X 2 = X β − A 2 ⋅ D β X ( t + 1 ) = X 1 + X 2 2 \begin{array}{l} D_{\alpha}=\left|\boldsymbol{C}_{1} \cdot X_{\alpha}-X\right|, D_{\beta}=\left|\boldsymbol{C}_{2} \cdot X_{\beta}-X\right| \\ X_{1}=X_{\alpha}-A_{1} \cdot D_{\alpha}, X_{2}=X_{\beta}-A_{2} \cdot D_{\beta} \\ X(t+1)=\frac{X_{1}+X_{2}}{2} \end{array} Dα=∣C1⋅Xα−X∣,Dβ=∣C2⋅Xβ−X∣X1=Xα−A1⋅Dα,X2=Xβ−A2⋅DβX(t+1)=2X1+X2
本研究使用随机值大于 1 或小于 -1 的 A’来强制使灰狼的头狼数量为 4. 若 A’∈[1,-1],则头狼数量为 2. 下一代个体更新公式为,
X ( t + 1 ) = { X 1 + X 2 + X 3 + X 4 4 , ∣ A 1 ⩾ 1 X 1 + X 2 2 , ∣ A ∣ < 1 X(t+1)=\left\{\begin{array}{l} \frac{X_{1}+X_{2}+X_{3}+X_{4}}{4}, \mid \boldsymbol{A}^{1} \geqslant 1 \\ \frac{X_{1}+X_{2}}{2},|\boldsymbol{A}|<1 \end{array}\right. X(t+1)={
4X1+X2+X3+X4,∣A1⩾12X1+X2,∣A∣<1
理论上,由于 AL-GWO 考虑到了算法的开发和勘探能力,它可以被视为一个全局优化算法. 搜索向量 A’的自适应变化使 AL-GWO 能够在勘探和开发之间顺利过渡. 在迭代前期,大部分|A’|≥1,此时头狼越多则勘探能力越大. 在迭代后期,大部分|A’| <1,此时头狼越少则开发能力越强.
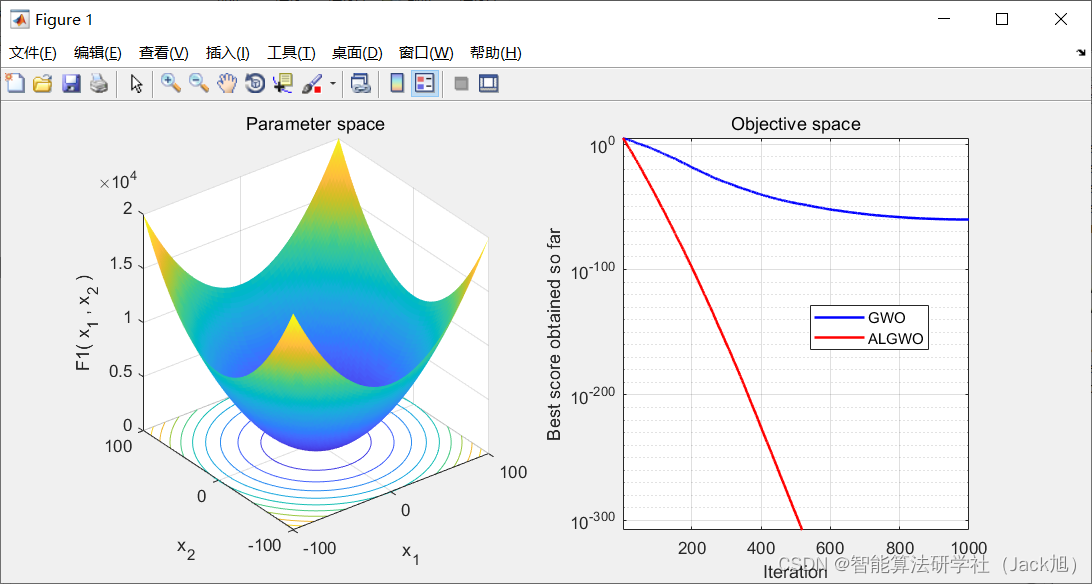
3.实验结果
4.参考文献
[1]郭阳,张涛,胡玉蝶,杜航.基于自适应头狼的灰狼优化算法[J].成都大学学报(自然科学版),2020,39(01):60-63+73.