15.1
试求矩阵
A = [ 1 2 0 2 0 2 ] A=\left[\begin{array}{lll}1 & 2 & 0 \\ 2 & 0 & 2\end{array}\right] A=[122002]
的奇异值分解。
手算了一下结果,
U = 1 5 [ 1 2 2 − 1 ] , Σ = [ 3 0 0 0 2 0 ] , V T = 1 5 [ 5 3 2 3 4 3 0 2 − 1 − 2 1 2 ] U = \frac{1}{\sqrt{5}}\left[\begin{array}{ll}1 & 2 \\ 2 & -1 \end{array}\right], \Sigma = \left[\begin{array}{lll}3 & 0 & 0 \\ 0 & 2 & 0 \end{array}\right], V^{T} = \frac{1}{\sqrt{5}}\left[\begin{array}{lll}\frac{5}{3} & \frac{2}{3} & \frac{4}{3} \\ 0 & 2 & -1 \\ -2 & 1 & 2\end{array}\right] U=51[122−1],Σ=[300200],VT=51⎣⎡350−2322134−12⎦⎤
验证一下:
import numpy as np
U = 1 / np.sqrt(5) * np.array([[1, 2], [2, -1]])
Sigma = np.array([[3, 0, 0], [0, 2, 0]])
V_transpose = 1 / np.sqrt(5) * np.array([[5/3, 2/3, 4/3], [0, 2, -1], [-2, 1, 2]])
U @ Sigma @ V_transpose
array([[1., 2., 0.],
[2., 0., 2.]])
看一下numpy中自带的分解:
A = np.array([[1, 2, 0], [2, 0, 2]])
U, Sigma, V_transpose = np.linalg.svd(A)
print('U:\n', U)
print('Sigma:\n', Sigma)
print('V_transpose:\n', V_transpose)
U:
[[ 0.4472136 -0.89442719]
[ 0.89442719 0.4472136 ]]
Sigma:
[3. 2.]
V_transpose:
[[ 7.45355992e-01 2.98142397e-01 5.96284794e-01]
[ 1.94726023e-16 -8.94427191e-01 4.47213595e-01]
[-6.66666667e-01 3.33333333e-01 6.66666667e-01]]
1 / np.sqrt(5) * np.array([[1, 2], [2, -1]]) # 手算的U
array([[ 0.4472136 , 0.89442719],
[ 0.89442719, -0.4472136 ]])
1 / np.sqrt(5) * np.array([[5/3, 2/3, 4/3], [0, 2, -1], [-2, 1, 2]]) # 手算的V转置
array([[ 0.74535599, 0.2981424 , 0.59628479],
[ 0. , 0.89442719, -0.4472136 ],
[-0.89442719, 0.4472136 , 0.89442719]])
可以发现,numpy自带的分解,左奇异矩阵矩阵第二个基和手算的结果差一个符号,显示了分解时基的选择不唯一,对应的V.T的第二行也是相差负号,而对于V.T的第三行是一个A零空间的基,我的选择不是很严格,只是满足在零空间中,而numpy的计算不知保证了V.T的行正交,好保证其列正交,但事实我们的基向量方向是相同的,这个自由度在还原A时不构成印象,正如上面验证的。
15.2
试求矩阵
A = [ 2 4 1 3 0 0 0 0 ] A=\left[\begin{array}{ll}2 & 4 \\ 1 & 3 \\ 0 & 0 \\ 0 & 0\end{array}\right] A=⎣⎢⎢⎡21004300⎦⎥⎥⎤
的奇异值分解并写出其外积展开式。
这个 A T A A^{T}A ATA的本征值时无理数,手算就有点繁琐了,所以直接用代码求解了:
15 - np.sqrt(13*17), 15 + np.sqrt(13*17) # 上述的两个本征值
(0.13393125268149397, 29.866068747318508)
A = np.array([[2, 4], [1, 3], [0, 0], [0, 0]])
U, Sigma, V_transpose = np.linalg.svd(A)
print('U:\n', U)
print('Sigma:\n', Sigma)
print('V_transpose:\n', V_transpose)
U:
[[-0.81741556 -0.57604844 0. 0. ]
[-0.57604844 0.81741556 0. 0. ]
[ 0. 0. 1. 0. ]
[ 0. 0. 0. 1. ]]
Sigma:
[5.4649857 0.36596619]
V_transpose:
[[-0.40455358 -0.9145143 ]
[-0.9145143 0.40455358]]
所以原矩阵是两个外积的叠加,第一个外积为:
first_item = Sigma[0] * U[:, 0][:, None] @ V_transpose[0][None, :]
first_item
array([[1.80720735, 4.08528566],
[1.27357371, 2.87897923],
[0. , 0. ],
[0. , 0. ]])
第二个外积为:
second_item = Sigma[1] * U[:, 1][:, None] @ V_transpose[1][None, :]
second_item
array([[ 0.19279265, -0.08528566],
[-0.27357371, 0.12102077],
[ 0. , 0. ],
[ 0. , 0. ]])
看看加和结果与原来是否相等:
A == first_item + second_item
array([[ True, True],
[ True, True],
[ True, True],
[ True, True]])
15.3
比较矩阵的奇异值分解与对称矩阵的对角化的异同。
相同:
都需要进行特征值、特征向量的计算;
特征值都是非负的;
正特征值的个数都等于原矩阵的秩;
特征值对应的特征向量都是正交的。
不同:
奇异值分解求解的特征值特征向量不是原矩阵的,而是原矩阵与其转置乘积构成的对称阵的;
对称矩阵对角化只需要求一次特征值特征向量,奇异值分解求一次只能得到左或右奇异矩阵其中一边的部分列向量,需要求解两次特征值特征向量,或者由左右奇异矩阵列向量的对应关系,由一遍求出另一边,最后还要对求零空间的标准正交基,以补全左右奇异矩阵;
对于奇异值分解,零空间中的矩阵存在一定自由度,因此使得U的行之间有可能出现不正交, V T V^{T} VT的列之间可能出现不正交(当然可以选择更严格点正交的值)。而对对称矩阵对角化,是正交的。
15.4
证明任何一个秩为1的矩阵可以写成两个向量的外积形式,并给出实例。
证明一:
如果一个矩阵秩为1,那么由线性代数初等变换的知识可知,必然存在某一矩阵的列向量,通过乘以某个系数,与其他任意一列相等,从而可以相减消掉其他列,也就是说该矩阵列向量都仅为这个列向量的某一系数倍,从而该列向量外积一个对应每列系数的行向量就得到该矩阵。(实例随便凑凑吧)
证明二:
如果矩阵的秩为1,那么其奇异值分解对角矩阵只有第一个主对角元 σ 1 \sigma_{1} σ1非0,其余元素都为0,则 A = U Σ V T A=U\Sigma V^{T} A=UΣVT变为 A = u 1 σ 1 v 1 T A=u_{1}\sigma_{1}v_{1}^{T} A=u1σ1v1T,其中 u 1 u_{1} u1和 v 1 T v_{1}^{T} v1T为 U U U的第一列和 V T V^{T} VT的第一行。由于矩阵的奇异值分解一定存在,而此时的分解即为向量外积,因此秩为1的矩阵一定存在两个向量的外积形式。
15.5
搜索中的点击数据记录用户搜索时提交的查询语句,点击的网页URL,以及点击次数,构成一个二部图,其中一个节点集合 { q i } \{q_{i}\} {
qi}表示查询,另一节点集合 { u j } \{u_{j}\} {
uj}表示URL,边表示点击关系,边上权重表示点击次数。如下图点击数据例子。点击数据可以由矩阵表示,试对其进行奇异值分解,并解释得到的三个矩阵表示的内容。
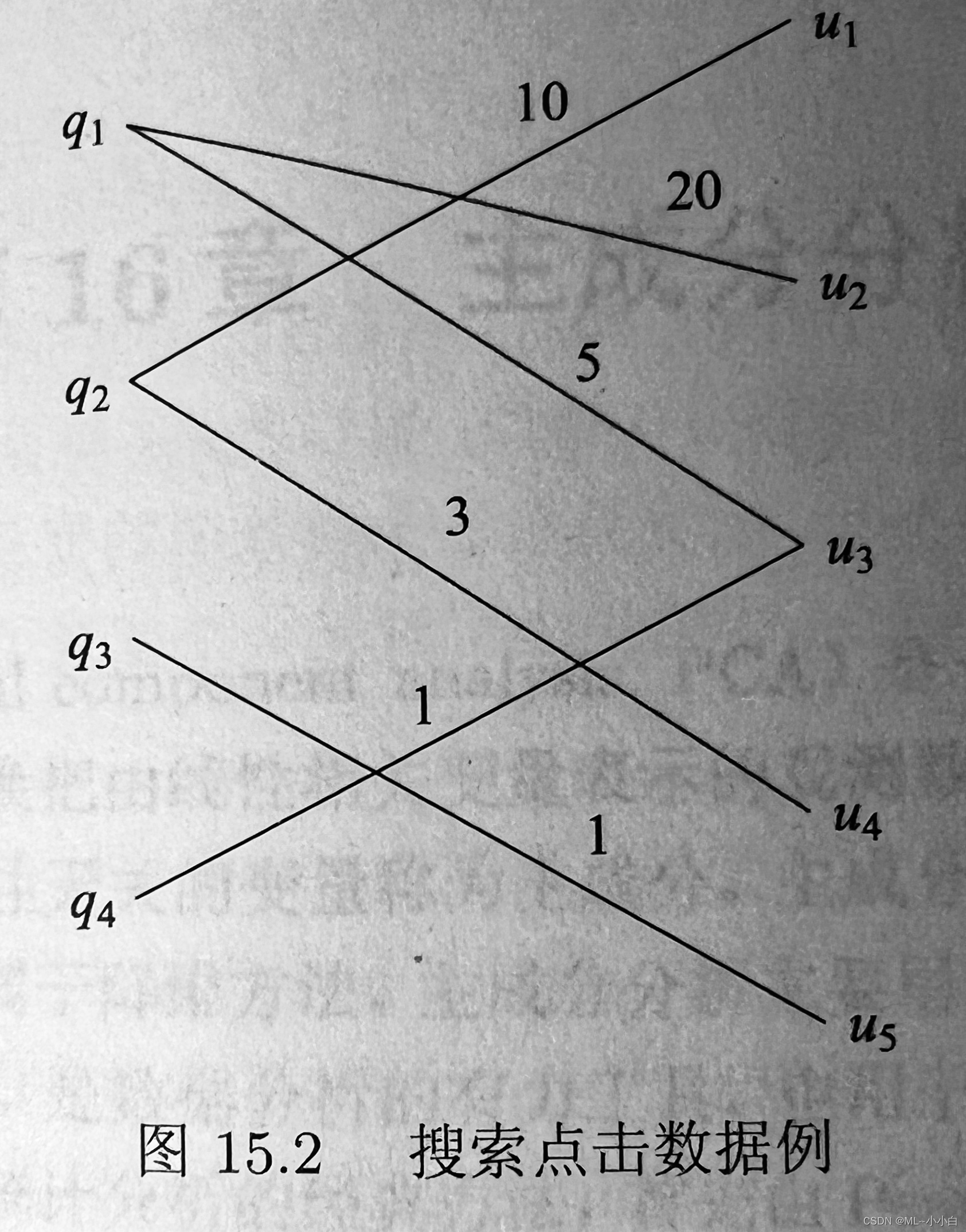
# 构造数据矩阵
A = np.array([[0, 20, 5, 0, 0],
[10, 0, 0, 3, 0],
[0, 0, 0, 0, 1],
[0, 0, 1, 0, 0]])
U, Sigma, V_transpose = np.linalg.svd(A)
print('U:\n', U)
print('Sigma:\n', Sigma)
print('V_transpose:\n', V_transpose)
U:
[[ 9.99930496e-01 -1.01352447e-16 0.00000000e+00 -1.17899939e-02]
[ 0.00000000e+00 1.00000000e+00 0.00000000e+00 -8.65973959e-15]
[ 0.00000000e+00 0.00000000e+00 1.00000000e+00 0.00000000e+00]
[ 1.17899939e-02 8.65973959e-15 0.00000000e+00 9.99930496e-01]]
Sigma:
[20.61695792 10.44030651 1. 0.97007522]
V_transpose:
[[ 0.00000000e+00 9.70007796e-01 2.43073808e-01 0.00000000e+00
0.00000000e+00]
[ 9.57826285e-01 -2.31404926e-16 8.02571613e-16 2.87347886e-01
0.00000000e+00]
[-0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00
1.00000000e+00]
[-7.97105437e-16 -2.43073808e-01 9.70007796e-01 0.00000000e+00
0.00000000e+00]
[ 2.87347886e-01 -1.01402229e-16 2.10571835e-16 -9.57826285e-01
0.00000000e+00]]
为了更方便观察,给出:

解释:
可以看前两个奇异值比后面两个大很多,参考在上面思维导图中,叙述的奇异值分解的几何意义以及外积表示的物理意义,可以这样分析。这个点击的数据矩阵中主要的贡献来自前两个奇异值对应的模式。对于第一个模式,看U的第一列,其基的方向主要在第一个元素,这个就是原本A矩阵的值域空间的基向量,这个向量对应最大的奇异值,表示这个基是query中这个模式主要贡献者,而且主要来自原来的A矩阵的表象的第一个贡献,即 q 1 q_{1} q1的贡献,之后其对应的 V T V^{T} VT的第一行,其表示A的行空间的基向量,这个基向量主要在原本A表象下第二个坐标的方向,即 u 2 u_{2} u2,说明这个模式中,在url空间中 u 2 u_{2} u2方向的数据,线性变换后主要成为query空间中 q 1 q_{1} q1方向的数据。同理,对于第二个奇异值的模式,类似分析可得,在url空间中 u 1 u_{1} u1方向的数据,线性变换后主要成为query空间中 q 2 q_{2} q2方向的数据。
综上,可以得到,这个数据矩阵,主要的贡献来自两种模式,第一种模式主要的贡献成分是 q 1 q_{1} q1到 u 2 u_{2} u2,第二种模式主要贡献成分为 q 2 q_{2} q2到 u 1 u_{1} u1,因为这个二部图不复杂,正如图中可以直观看到的那样,主要的模式是20,10权重的,20的模式对应的就是 q 1 q_{1} q1到 u 2 u_{2} u2,10的模式对应的就是 q 2 q_{2} q2到 u 1 u_{1} u1。
可以验证一下上面的解释:
first_item = Sigma[0] * U[:, 0][:, None] @ V_transpose[0][None, :]
first_item
array([[ 0. , 19.99721992, 5.01109415, 0. , 0. ],
[ 0. , 0. , 0. , 0. , 0. ],
[ 0. , 0. , 0. , 0. , 0. ],
[ 0. , 0.23578349, 0.05908488, 0. , 0. ]])
second_item = Sigma[1] * U[:, 1][:, None] @ V_transpose[1][None, :]
second_item[second_item<0.001] = 0
second_item
array([[ 0., 0., 0., 0., 0.],
[10., 0., 0., 3., 0.],
[ 0., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0.]])
third_item = Sigma[2] * U[:, 2][:, None] @ V_transpose[2][None, :]
third_item[third_item<0.001] = 0
third_item
array([[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 1.],
[0., 0., 0., 0., 0.]])
fourth_item = Sigma[3] * U[:, 3][:, None] @ V_transpose[3][None, :]
fourth_item[fourth_item<0.001] = 0
fourth_item
array([[0. , 0.00278008, 0. , 0. , 0. ],
[0. , 0. , 0. , 0. , 0. ],
[0. , 0. , 0. , 0. , 0. ],
[0. , 0. , 0.94091512, 0. , 0. ]])