目录
低通 FIR 滤波器 - 加窗方法
此示例说明如何使用两个命令行函数 fir1 和 designfilt 以及交互式滤波器设计工具来设计和实现 FIR 滤波器。
创建要在示例中使用的信号。该信号是 N(0,1/4) 加性高斯白噪声中的 100 Hz 正弦波。将随机数生成器设置为默认状态,以获得可重现的结果。
rng default
Fs = 1000;
t = linspace(0,1,Fs);
x = cos(2*pi*100*t)+0.5*randn(size(t));要设计的滤波器是阶数等于20、截止频率为150Hz 的FIR低通滤波器。使用Kaiser窗,其长度比滤波器阶和 β=3 多一个样本。
使用fir1设计滤波器。fir1需要区间 [0, 1] 内的归一化频率,其中 1 对应于 π 弧度/采样点。要使用fir1,必须将所有频率设定转换为归一化频率。
设计滤波器并查看滤波器的幅值响应。
fc = 150;
Wn = (2/Fs)*fc;
b = fir1(20,Wn,'low',kaiser(21,3));
fvtool(b,1,'Fs',Fs)如图所示:
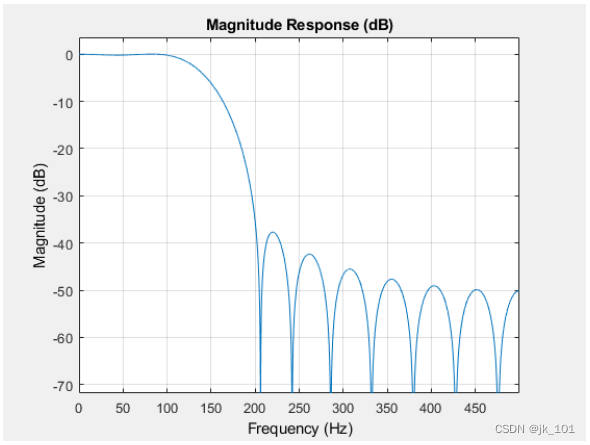
将滤波器应用于信号,并绘制 100 Hz 正弦波的前十个周期的结果。
y = filter(b,1,x);
plot(t,x,t,y)
xlim([0 0.1])
xlabel('Time (s)')
ylabel('Amplitude')
legend('Original Signal','Filtered Data')如图所示:
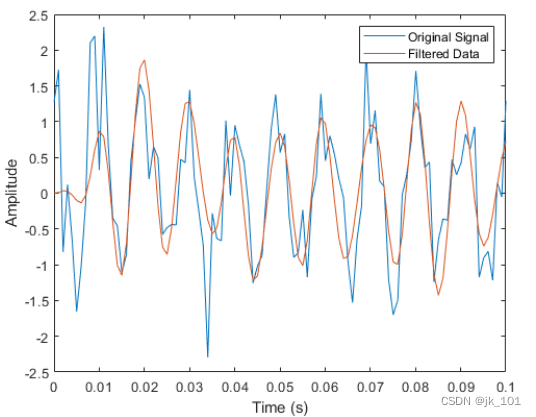
使用 designfilt 设计相同的滤波器。将滤波器响应设置为 'lowpassfir',并以 Name,Value 对组形式输入设定。使用 designfilt 时,可以以 Hz 为单位指定滤波器设计。
Fs = 1000;
Hd = designfilt('lowpassfir','FilterOrder',20,'CutoffFrequency',150, ...
'DesignMethod','window','Window',{@kaiser,3},'SampleRate',Fs);对数据进行滤波并绘制结果。
y1 = filter(Hd,x);
plot(t,x,t,y1)
xlim([0 0.1])
xlabel('Time (s)')
ylabel('Amplitude')
legend('Original Signal','Filtered Data')如图所示:
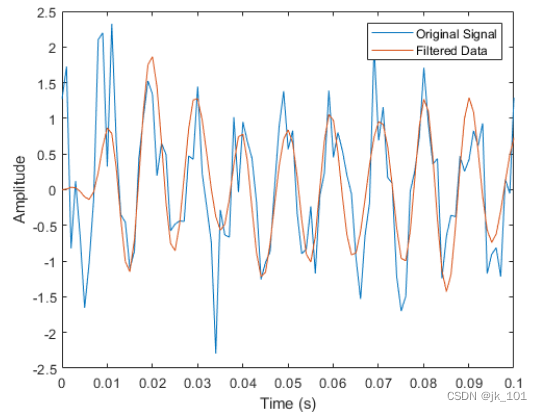
使用滤波器设计工具设计低通 FIR 滤波器
此示例说明如何使用加窗方法和交互式滤波器设计工具设计和实现低通 FIR 滤波器。
-
在命令行中输入 filterDesigner 启动滤波器设计工具。
-
将响应类型设置为低通。
-
将设计方法设置为 FIR,并选择窗口方法。
-
在滤波器阶数下,选择指定阶数。将阶设置为 20。
-
在频率设定下,将单位设置为 Hz,将 Fs 设置为 1000,并将 Fc 设置为 150。

-
点击设计滤波器。
-
选择文件 > 导出...,将您的 FIR 滤波器作为系数或滤波器对象导出到 MATLAB® 工作区。在本示例中,将滤波器导出为对象。将变量名称指定为Hd。
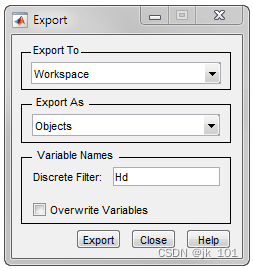
-
点击导出。
-
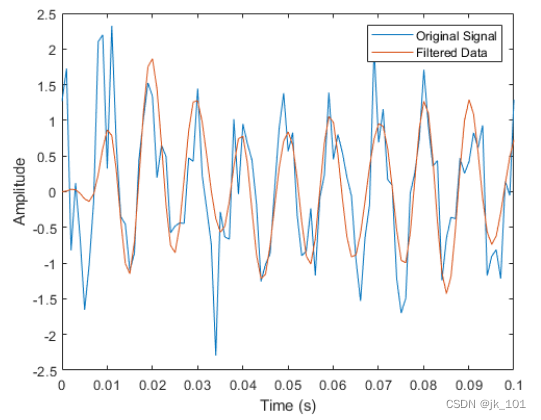
用导出的滤波器对象对命令行窗口中的输入信号进行滤波。绘制 100 Hz 正弦波的前十个周期的结果。
y2 = filter(Hd,x);
plot(t,x,t,y2)
xlim([0 0.1])
xlabel('Time (s)')
ylabel('Amplitude')
legend('Original Signal','Filtered Data')如图所示:
-
选择文件 > 生成 MATLAB 代码 > 滤波器设计函数生成使用您的设定创建滤波器对象的 MATLAB 函数。
也可以使用交互式工具 filterBuilder 来设计您的滤波器。
带通滤波器 - 最小阶 FIR 和 IIR 系统
此示例说明如何设计带通滤波器,并使用最小阶 FIR 等波纹滤波器和 IIR Butterworth 滤波器对数据进行滤波。可以将许多真实世界的信号建模为振荡分量、低频趋势和加性噪声的叠合。例如,经济数据通常包含振荡,这表示周期叠加在缓慢变化的上升或下降趋势上。此外,还有加性噪声分量,即测量误差和过程中固有的随机波动的组合。
在这些示例中,假设连续一年每天都对一些过程进行采样。假设该过程在大约一周和一个月的范围内有振荡。此外,数据和 N(0,1/4) 加性高斯白噪声中存在低频上升趋势。
将信号创建为频率为 1/7 和 1/30 周期/天的两个正弦波的叠加。添加低频增长趋势项和 N(0,1/4) 高斯白噪声。重置随机数生成器以获得可重现的结果。数据以 1 个采样点/天进行采样。绘制结果信号和功率频谱密度 (PSD) 估计。
rng default
Fs = 1;
n = 1:365;
x = cos(2*pi*(1/7)*n)+cos(2*pi*(1/30)*n-pi/4);
trend = 3*sin(2*pi*(1/1480)*n);
y = x+trend+0.5*randn(size(n));
[pxx,f] = periodogram(y,[],[],Fs);
subplot(2,1,1)
plot(n,y)
xlim([1 365])
xlabel('Days')
grid
subplot(2,1,2)
plot(f,10*log10(pxx))
xlabel('Cycles/day')
ylabel('dB')
grid如图所示:

在功率频谱密度估计中,低频趋势表现为低频功率增加。低频功率比 1/30 周期/天的振荡高约 10 dB。在滤波器阻带设定中使用此信息。
设计具有以下设定的最小阶 FIR 等波纹滤波器和 IIR Butterworth 滤波器:通带从 [1/40,1/4] 周期/天开始,阻带从 [0,1/60] 周期/天和 [1/4,1/2] 周期/天开始。将阻带衰减都设为 10 dB,将通带波纹容差设为 1 dB。
Hd1 = designfilt('bandpassfir', ...
'StopbandFrequency1',1/60,'PassbandFrequency1',1/40, ...
'PassbandFrequency2',1/4 ,'StopbandFrequency2',1/2 , ...
'StopbandAttenuation1',10,'PassbandRipple',1, ...
'StopbandAttenuation2',10,'DesignMethod','equiripple','SampleRate',Fs);
Hd2 = designfilt('bandpassiir', ...
'StopbandFrequency1',1/60,'PassbandFrequency1',1/40, ...
'PassbandFrequency2',1/4 ,'StopbandFrequency2',1/2 , ...
'StopbandAttenuation1',10,'PassbandRipple',1, ...
'StopbandAttenuation2',10,'DesignMethod','butter','SampleRate',Fs);比较 FIR 和 IIR 滤波器的阶数以及展开的相位响应。
fprintf('The order of the FIR filter is %d\n',filtord(Hd1))
The order of the FIR filter is 78
fprintf('The order of the IIR filter is %d\n',filtord(Hd2))
The order of the IIR filter is 8
%%
[phifir,w] = phasez(Hd1,[],1);
[phiiir,w] = phasez(Hd2,[],1);
figure
plot(w,unwrap(phifir))
hold on
plot(w,unwrap(phiiir))
hold off
xlabel('Cycles/Day')
ylabel('Radians')
legend('FIR Equiripple Filter','IIR Butterworth Filter')
grid如图所示:
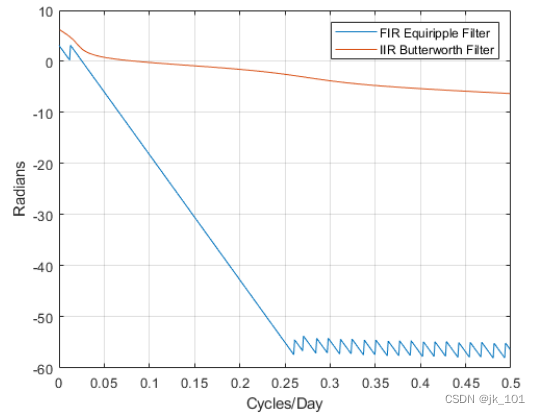
IIR 滤波器的阶数比 FIR 滤波器低得多。然而,FIR 滤波器在通带上具有线性相位响应,而 IIR 滤波器则没有。FIR 滤波器以均等的方式延迟滤波器通带中的所有频率,而 IIR 滤波器不延迟。
此外,单位频率的相位变化率在 FIR 滤波器中比在 IIR 滤波器中大。
设计一个低通 FIR 等波纹滤波器进行比较。低通滤波器设定为:通带 [0,1/4] 周期/天,阻带衰减等于 10 dB,通带波纹容差设置为 1 dB。
Hdlow = designfilt('lowpassfir', ...
'PassbandFrequency',1/4,'StopbandFrequency',1/2, ...
'PassbandRipple',1,'StopbandAttenuation',10, ...
'DesignMethod','equiripple','SampleRate',1);用带通滤波器和低通滤波器对数据进行滤波。
yfir = filter(Hd1,y);
yiir = filter(Hd2,y);
ylow = filter(Hdlow,y);绘制带通 IIR 滤波器输出的 PSD 估计值。可以将以下代码中的yiir 替换为 yfir 以查看 FIR 带通滤波器输出的 PSD 估计值。
[pxx,f] = periodogram(yiir,[],[],Fs);
plot(f,10*log10(pxx))
xlabel('Cycles/day')
ylabel('dB')
grid如图所示:
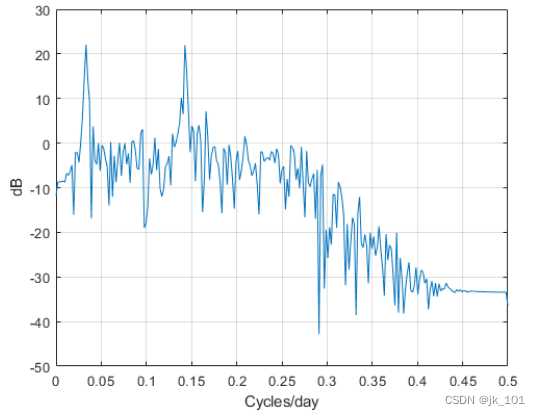
PSD 估计值显示带通滤波器使低频趋势和高频噪声发生了衰减。绘制前 120 天的 FIR 和 IIR 滤波器输出。
plot(n,yfir,n,yiir)
axis([1 120 -2.8 2.8])
xlabel('Days')
legend('FIR bandpass filter output','IIR bandpass filter output', ...
'Location','SouthEast')
如图所示:

FIR 滤波器中增加的相位延迟在滤波器输出中很明显。
在 7 天和 30 天周期的叠加图上再叠加绘制低通 FIR 滤波器输出,以进行比较。
plot(n,x,n,ylow)
xlim([1 365])
xlabel('Days')
legend('7-day and 30-day cycles','FIR lowpass filter output', ...
'Location','NorthWest')如图所示:

从上图中可以看出,低频趋势在低通滤波器输出中很明显。虽然低通滤波器保留 7 天和 30 天的周期,但在本例中,带通滤波器性能更好,因为带通滤波器还消除了低频趋势。
零相位滤波
此示例说明如何执行零相位滤波。使用 fir1 和 designfilt 重复信号生成和低通滤波器设计。如果工作区中已有这些变量,则不必执行以下代码。
rng default
Fs = 1000;
t = linspace(0,1,Fs);
x = cos(2*pi*100*t)+0.5*randn(size(t));
% Using fir1
fc = 150;
Wn = (2/Fs)*fc;
b = fir1(20,Wn,'low',kaiser(21,3));
% Using designfilt
Hd = designfilt('lowpassfir','FilterOrder',20,'CutoffFrequency',150, ...
'DesignMethod','window','Window',{@kaiser,3},'SampleRate',Fs);使用 filter 对数据进行滤波。绘制滤波器输出的前 100 个点以及幅值和初始相位与输入信号相同的叠加正弦波。
yout = filter(Hd,x);
xin = cos(2*pi*100*t);
plot(t,xin,t,yout)
xlim([0 0.1])
xlabel('Time (s)')
ylabel('Amplitude')
legend('Input Sine Wave','Filtered Data')
grid如图所示:
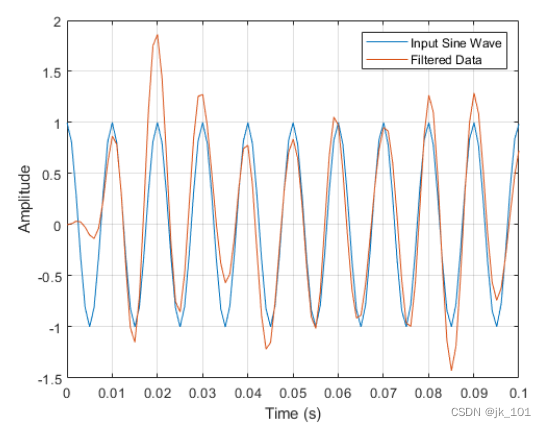
查看最初 0.01 秒的滤波后数据,您会发现输出相对于输入有所延迟。延迟大约为 0.01 秒,几乎是 FIR 滤波器长度的 1/2,用采样长度表示为 (10×0.001)。
这种延迟是滤波器的相位响应造成的。这些示例中的 FIR 滤波器是一种 I 类线性相位滤波器。滤波器的群延迟是 10 个采样点。
使用 fvtool 对群延迟绘图。
fvtool(Hd,'Analysis','grpdelay')如图所示:
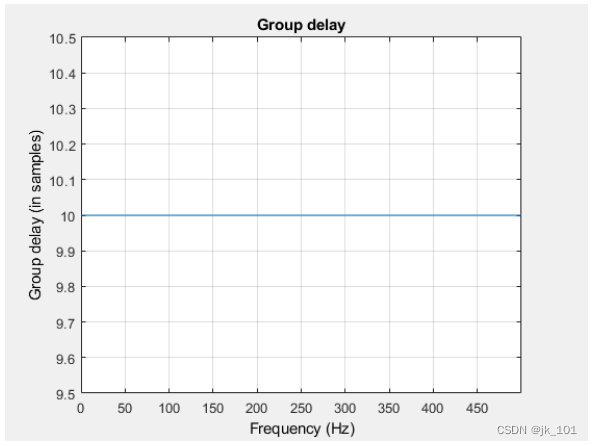
在许多应用中,相位失真是可以接受的。当相位响应为线性时,尤其如此。在其他应用中,希望滤波器具有零相位响应。非因果滤波器理论上无法实现零相位响应。但是,可以结合使用因果滤波器和 filtfilt 来实现零相位滤波。
使用 filtfilt 对输入信号进行滤波。对响应绘图,比较使用 filter 和 filtfilt 获得的滤波器输出。
yzp = filtfilt(Hd,x);
plot(t,xin,t,yout,t,yzp)
xlim([0 0.1])
xlabel('Time (s)')
ylabel('Amplitude')
legend('100-Hz Sine Wave','Filtered Signal','Zero-phase Filtering',...
'Location','NorthEast')如图所示:

在上图中,可以看到 filtfilt 的输出没有表现出由 FIR 滤波器相位响应造成的延迟。