从Logistic Regression 到 Neural Network

Logistic Regression to Neural Network

Logistic Regression 可以看作是一个没有隐藏层的 Neural Network
Neural Network 可以看作是有多个Logistic Regression 堆叠而成的
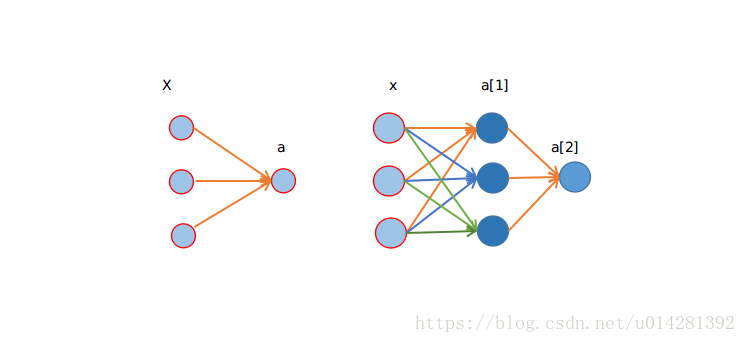
1. Logistic Regression
1. Neural Network with one hidden layer

１．Logistic Regression

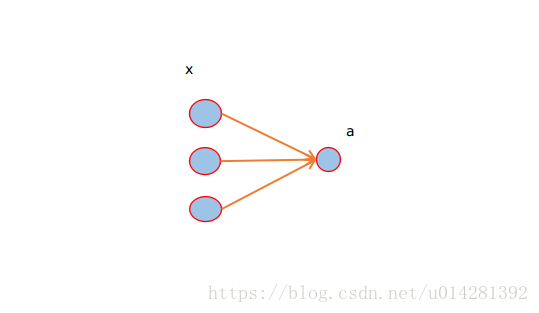
这里写图片描述
上图是一个Logistic Regression模型的结构图

$x$ : 模型的输入，是一个样本的特征向量，shape=(3,1)
$w$ : 连接输入和输出之间的权值矩阵，shape=(3,1)
$b$ ：偏置,shape(1,)
$a$ ：模型的最终输出，要经过非线性函数 $\sigma$ 的＇激活＇
$\sigma$ : $\sigma = \frac{1}{1+e^{-(wx+b)}}$

1.1 Forward propagate

\begin{matrix} (1) & z = w^{T} x + b \end{matrix}

$z = w^Tx+b \tag{1}$

\begin{matrix} (2) & \hat{y} = a = σ (z) \end{matrix}

$\hat{y} = a = \sigma(z) \tag{2}$

1.2 Object function(cost function)

\begin{matrix} (3) & J = - (y l o g (\hat{y}) + (1 - y) l o g (1 - \hat{y})) \end{matrix}

$J = -\large\left(ylog\small(\hat{y}) + (1-y)log(1-\hat{y})\large\right)\tag{3}$

1.3 Backward propagate

1, $d_w = \frac{\partial{J}}{\partial{a}}.\frac{\partial{a}}{\partial{z}}.\frac{\partial{z}}{\partial{w}} = ?$

2， $d_b = \frac{\partial{J}}{\partial{a}}.\frac{\partial{a}}{\partial{z}} = ?$

$\frac{\partial{J}}{a} = -\frac{y}{a}+\frac{1-y}{1-a} = \frac{a-y}{a(1-a)}$
$\frac{\partial{a}}{z} = a(1-a)$
$\frac{\partial{z}}{w} = x$
$\begin{matrix} (4) & d_{w} = (a - y) x \end{matrix}$ $d_w = (a-y)x\tag{4}$
$\begin{matrix} (5) & d_{b} = a - y \end{matrix}$ $d_b = a-y\tag{5}$
$\begin{matrix} (6) & w = w - α d_{w} \end{matrix}$ $w = w - \alpha d_w\tag{6}$
$\begin{matrix} (7) & b = b = α d_{b} \end{matrix}$ $b = b = \alpha d_b\tag{7}$

1.4 Explanation Cost Function

关于cost function 我们约定： $\hat{y} = p(y = 1 | x)$

$\hat{y}$ : 在给定训练样本 $x$ 的条件下，y = 1的概率, $1 - \hat{y}$ : y = 0的概率
$y = 1 : p(y|x) = \hat{y}$
$y = 0 : p(y|x) = 1 - \hat{y}$

在２分类问题当中， $p(y|x)$ ,包含两种情况 y = 0 或　y = 1,所以两个条件概率合并如下：

\begin{matrix} (8) & p (y | x) = {\hat{y}}^{y} (1 - \hat{y})^{(1 - y)} \end{matrix}

$p(y|x) = \hat{y}^{y}(1-\hat{y})^{(1-y)}\tag{8}$

$y = 1，\hat{y}^{y} = \hat{y}，(1-\hat{y})^{(1-y)} = 1，p(y|x) = \hat{y}$
$y = 0，\hat{y}^{y} = 1，(1-\hat{y})^{(1-y)} = 1-\hat{y}，p(y|x) = 1 - \hat{y}$
$log()$ 是严格的单调递增函数，最大化 $log(p(y|x))$ 等价与最大化 $p(y|x)$ .
$log(p(y|x)) = log(\hat{y}^{y}(1-\hat{y})^{(1-y)})\tag{9}$
化简后： $ylog(\hat{y})+(1-y)log(1-\hat{y})$

$J = -L(\hat{y},y)$

加负号的原因：

扫描二维码关注公众号，回复： 1439867 查看本文章
- 训练模型时需要输出的概率值最大
- 逻辑回归中要最小化损失函数

2. Neural Network

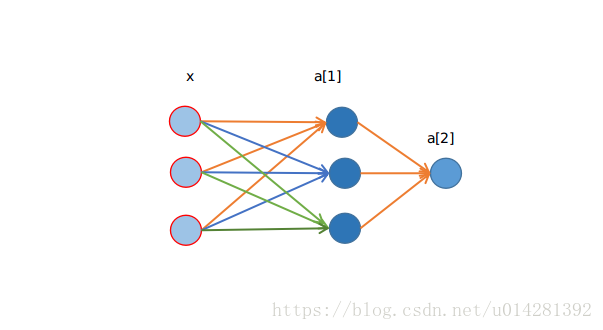
这里写图片描述
上图所示，是一个三层的网络结构，输入层神经元数量为 $n^{[0]}$ ，隐藏层为 $n^{[1]}$ ，输出层为 $n^{[2]}$ ．

$n^{[0]}$ : 3
$n^{[1]}$ : 3
$n^{[2]}$ : 1
$x = a^{[0]}$ : 输入样本的特征向量 $a^{[0]}$ ，shape=( $n^{[0]}$ ，１)
$w^{[1]}$ : 连接输入层和隐藏层之间的权值矩阵，shape=( $n^{[0]}$ , $n^{[1]}$ )
$b^{[1]}$ : 偏置，可以是一个标量，numpy中的＇广播＇机制会传递给矩阵或向量中的每一个元素，shape=(1,)
$a^{[1]}$ : 隐藏层的输出，shape=( $n^{[1]}$ , 1)
$w^{[2]}$ : 连接隐藏层和输出层之间的权值矩阵，shape=( $n^{[1]}$ , $n^{[2]}$ )
$b^{[2]}$ : 偏置
$a^{[2]}$ : 输出层的输出
$\sigma$ : $\sigma = \frac{1}{1+e^{-(wx+b)}}$

2.1 Forward propagate

$x$ 为一个样本的特征向量，shape=(3, 1)
$z^{[1]} = w^{[1]T}x + b^{[1]}\tag{1}$
$a^{[1]} = \sigma(z^{[1]})\tag{2}$
$z^{[2]} = w^{[2]T}a^{[1]} + b^{[2]}\tag{3}$
$a^{[2]} = \hat{y} = \sigma(z^{[2]})\tag{4}$
$J = -\large\left(ylog(a^{[2]}) + (1-y)log(1-a^{[2]})\large\right)\tag{5}$

2.2 Backward propagate

计算梯度

d_{w^{[2]}} = \frac{\partial J}{\partial a^{[2]}} . \frac{\partial a^{[2]}}{\partial z^{[2]}} . \frac{\partial z^{[2]}}{w^{[2]}}

$d_{w^{[2]}} = \frac{\partial{J}}{\partial{a^{[2]}}}.\frac{\partial{a^{[2]}}}{\partial{z^{[2]}}}.\frac{\partial{z^{[2]}}}{w^{[2]}}$

d_{b^{[2]}} = \frac{\partial J}{\partial a^{[2]}} . \frac{\partial a^{[2]}}{\partial z^{[2]}}

$d_{b^{[2]}} = \frac{\partial{J}}{\partial{a^{[2]}}}.\frac{\partial{a^{[2]}}}{\partial{z^{[2]}}}$

\frac{\partial J}{\partial a^{[2]}} = - \frac{y}{a^{[2]}} + \frac{1 - y}{1 - a^{[2]}} = \frac{a^{[2]} - y}{a^{[2]} (1 - a^{[2]})}

$\frac{\partial{J}}{\partial{a^{[2]}}} = -\frac{y}{a^{[2]}} + \frac{1-y}{1-a^{[2]}} = \frac{a^{[2]}-y}{a^{[2]}(1-a^{[2]})}$

\frac{\partial a^{[2]}}{\partial z^{[2]}} = a^{[2]} (1 - a^{[2]})

$\frac{\partial{a^{[2]}}}{\partial{z^{[2]}}} = a^{[2]}(1-a^{[2]})$

\frac{\partial z^{[2]}}{w^{[2]}} = a^{[1]}

$\frac{\partial{z^{[2]}}}{w^{[2]}} = a^{[1]}$

$d_{w^{[2]}} = \frac{a^{[2]}-y}{a^{[2]}(1-a^{[2]})}.a^{[2]}(1-a^{[2]}).a^{[1]} = (a^{[2]}-y)a^{[1]}\tag{6}$

$d_{b^{[2]}} = \frac{a^{[2]}-y}{a^{[2]}(1-a^{[2]})}.a^{[2]}(1-a^{[2]}) = a^{[2]}-y \tag{7}$

d_{w^{[1]}} = \frac{\partial J}{\partial a^{[2]}} . \frac{\partial a^{[2]}}{\partial z^{[2]}} . \frac{\partial z^{[2]}}{a^{[1]}} . \frac{\partial a^{[1]}}{\partial z^{[1]}} . \frac{\partial z^{[1]}}{w^{[1]}}

$d_{w^{[1]}} = \frac{\partial{J}}{\partial{a^{[2]}}}.\frac{\partial{a^{[2]}}}{\partial{z^{[2]}}}.\frac{\partial{z^{[2]}}}{a^{[1]}}.\frac{\partial{a^{[1]}}}{\partial{z^{[1]}}}.\frac{\partial{z^{[1]}}}{w^{[1]}}$

d_{b^{[1]}} = \frac{\partial J}{\partial a^{[2]}} . \frac{\partial a^{[2]}}{\partial z^{[2]}} . \frac{\partial z^{[2]}}{a^{[1]}} . \frac{\partial a^{[1]}}{\partial z^{[1]}}

$d_{b^{[1]}} = \frac{\partial{J}}{\partial{a^{[2]}}}.\frac{\partial{a^{[2]}}}{\partial{z^{[2]}}}.\frac{\partial{z^{[2]}}}{a^{[1]}}.\frac{\partial{a^{[1]}}}{\partial{z^{[1]}}}$

\frac{\partial z^{[2]}}{a^{[1]}} = w^{[2]}

$\frac{\partial{z^{[2]}}}{a^{[1]}} = w^{[2]}$

\frac{\partial a^{[1]}}{\partial z^{[1]}} = a^{[1]} (1 - a^{[1]})

$\frac{\partial{a^{[1]}}}{\partial{z^{[1]}}} = a^{[1]}(1-a^{[1]})$

\frac{\partial z^{[1]}}{w^{[1]}} = x

$\frac{\partial{z^{[1]}}}{w^{[1]}} = x$

$d_{w^{[1]}} = x\odot (((a^{[2]}-y)w^{[2]})\odot(a^{[1]}(1-a^{[1]})))^T\tag{8}$

$d_{b^{[1]}} = \frac{a^{[2]}-y}{a^{[2]}(1-a^{[2]})}.a^{[2]}(1-a^{[2]}).w^{[2]}.a^{[1]}(1-a^{[1]})=((a^{[2]}-y)w^{[2]})\odot (a^{[1]}(1-a^{[1]})) \tag{9}$

更新权值

$w^{[1]} = w^{[1]} - \alpha d_{w^{[1]}}\tag{10}$
$b^{[1]} = b^{[1]} - \alpha d_{b^{[1]}}\tag{11}$
$w^{[2]} = w^{[2]} - \alpha d_{w^{[2]}}\tag{12}$
$b^{[2]} = b^{[2]} - \alpha d_{b^{[2]}}\tag{13}$