基于信心上界蒙特卡洛搜索树(UCT)实现四子棋
算法
本次实验采用信心上界蒙特卡洛搜索树(UCT)实现,算法简要描述如下:
搜索树上每一个节点表示一个局面。对某节点 x,x 的第 i 个子节点
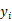
表示节点 x 的局面在第 i 列落子后形成的下一局面。以当前局面作为树根进行搜索。对于每个节点,统计经该节点及其子节点所表示的局面出发进行的所有博弈,记录博弈的总场数 n 及总获胜场数 m,则对该节点获胜概率的估计为
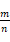
。为了估计出准确的获胜概率,需要进行足够多次的博弈试验。每次试验均从树根所表示的局面出发,执行如下策略:
若当前局面在搜索树上已被节点 x 表示,且由此局面落子一步产生的所有次局面,均已由 x 的子节点表示,则选择 UCB 信心上界最大的子节点所对应的落子。若记节点 x 记录的总试验次数和获胜次数分别为 n 和 m,x 的子节点
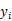

其中 c 为比例系数,本实验中 c=1,具体取值在后文有讨论。此处“获胜”指的是相对于当前节点所表示的玩家而言;
若当前局面在搜索树上已被节点 x 表示,但由此局面某一落子产生的次局面,并没有由 x 的子节点表示,则选择执行此落子,并在树上扩展出新的节点记录此新局面;
若当前局面在搜索树上没有被任何节点表示,则随机执行一落子。但 ① 若执行某落子可直接获胜,或 ② 不执行某落子将直接落负,则执行此落子。
每次试验后更新树上节点记录的信息。执行足够多次试验后,选择根节点的所有子节点中估计胜率
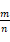
将收敛于真实胜率,择其最大的一项作为正式决策。
UCT 算法平衡了探索与利用:某策略尝试次数较少时,其信心上界较高,算法将尝试足够多陌生的决策(探索);某策略估计胜率较高时,其信心上界也高,算法将专注于这些策略,避免在胜率过小的局面上浪费过多计算量(利用)。
上述算法并非朴素的 UCT 算法,有如下两点改进值得注意:
- 若节点 x 还没有子节点,并非一次性扩展出其所有子节点,而是一个一个地扩展(见上述步骤 2),避免在扩展某一个节点时一次性浪费太多计算量。
- 步骤 3 并非随机策略,而是能感知下一步必胜或者必败的局面。判断必胜或必败并不需要花费多少计算量,但此举有效避免了纯粹随机策略的盲目性。
测量与评价
为了评价本算法,做了如下若干测量。虽然随机噪声较大,但也能说明一定问题。
蒙特卡洛算法需要试验次数达到一定后,估计胜率
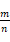
才能收敛于真实胜率。为了分析算法执行的试验次数是否足够,选择若干参照 AI 与之对弈,每组数据测量 20 轮游戏,其中一半作为先手,另一半作为后手。测量程序运行时间(正比于试验次数)与胜率的关系如下:
| 参照 AI;;运行时间 | 10.dll | 20.dll | 30.dll | 40.dll | 50.dll | 60.dll | 70.dll | 80.dll | 90.dll | 100.dll |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.5s | 1 | 1 | N/A | 1 | 0.95 | 0.95 | 0.95 | 0.85 | 0.95 | 0.85 |
| 1.0s | 1 | 1 | N/A | 1 | 0.95 | 1 | 1 | 1 | 0.95 | 0.65 |
| 1.5s | 1 | 1 | N/A | 0.9 | 1 | 1 | 0.95 | 1 | 1 | 0.6 |
| 2.0s | 1 | 0.95 | N/A | 1 | 1 | 0.95 | 0.85 | 1 | 1 | 0.75 |
| 2.5s | 1 | 0.95 | N/A | 1 | 1 | 0.95 | 1 | 0.95 | 1 | 0.75 |
可以看出,0.5s~2.5s 范围内,胜率与运行时间没有统计意义上的差异。可以认为试验次数已经足够。
UCB 信心上界式中有比例系数 c,为确定最佳的 c 取值,做以下测量。仍然每组数据测量 20 轮游戏,其中一半作为先手,另一半作为后手。
| 参照 AI;c | 70.dll | 80.dll | 90.dll | 100.dll |
|---|---|---|---|---|
| 0.1 | 0 | 0.1 | 0.05 | 0 |
| 0.4 | 0.9 | 1 | 0.85 | 0.55 |
| 0.7 | 0.95 | 0.95 | 1 | 0.75 |
| 1.0 | 1 | 0.85 | 0.95 | 0.8 |
| 1.3 | 1 | 1 | 1 | 0.7 |
| 1.6 | 1 | 0.95 | 0.95 | 0.5 |
| 1.9 | 0.95 | 0.9 | 0.75 | 0.6 |
绘制图像:

可以看出 c≤0.5 或 c≥1.5 时胜率显著下降,但 0.5<c<1.5 时胜率没有显著区别。本实验中选择 c=1 作为最终参数。
其他改进的尝试
除在“算法”一节所述的两点改进外,我还尝试了其他改进方法如下,但实验表明其效果不好,故没有被采用于最终版本中。
UCT 算法的一项缺点是:某一个较优的决策须被尝试足够次数后,其价值才能反映在估计胜率
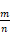
中,浪费了许多计算量。这是由于某一节点的胜率是由其所有子节点胜率的加权平均得来,而非其子节点胜率的最大值得来。
我试图将某节点的获胜可能设为随机变量,假设其服从正态分布 N(μ,σ),以 μ+σ 作为替代的信心上界进行蒙特卡洛搜索。每一节点的获胜可能定义为其子节点获胜可能的最大值。虽然若干正态分布的最大值所服从的分布并没有解析解,但可以通过简单函数拟合,通过此方法可估计出树上每一节点的获胜可能,最后选择获胜可能期望最大的决策。
实验表明,此方法胜率不如朴素算法。我认为可能由以下原因所致:
- “测量与评价”一节的分析表明,朴素算法中尝试次数已经足够,UCT 浪费的计算量并没有过多负面影响;
- 若干正态分布变量的最大值不再服从正态分布,按此方法估计会产生偏差。
关于代码实现的说明
代码中,Board 类用作管理当前局面,在搜索中维护落子位置及 top 位置的信息;Search 类用作执行 UCT 搜索。Strategy.cpp 用于与框架交互。
法估计会产生偏差。
关于代码实现的说明
代码中,Board 类用作管理当前局面,在搜索中维护落子位置及 top 位置的信息;Search 类用作执行 UCT 搜索。Strategy.cpp 用于与框架交互。