穷取法计算量太大,搜索空间太大,不太现实
分治算法,各个击破
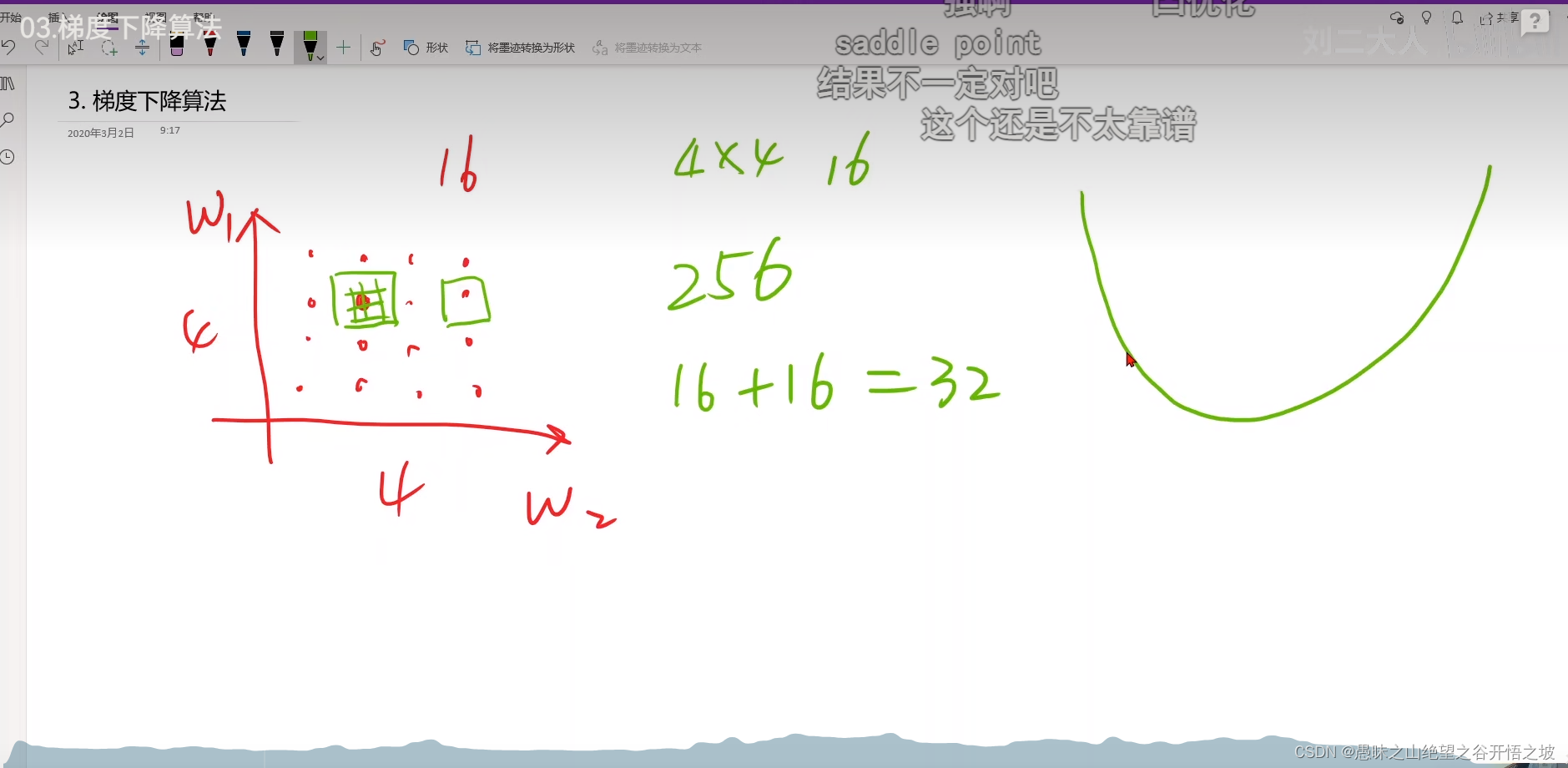
分治算法,不适合非凸函数,会陷入局部最优,凸函数,任取两点,画一条线段,线段的值都在曲线上面或者曲线下面,神经网络参数数量过大,划分空间去搜索也是没法划分的
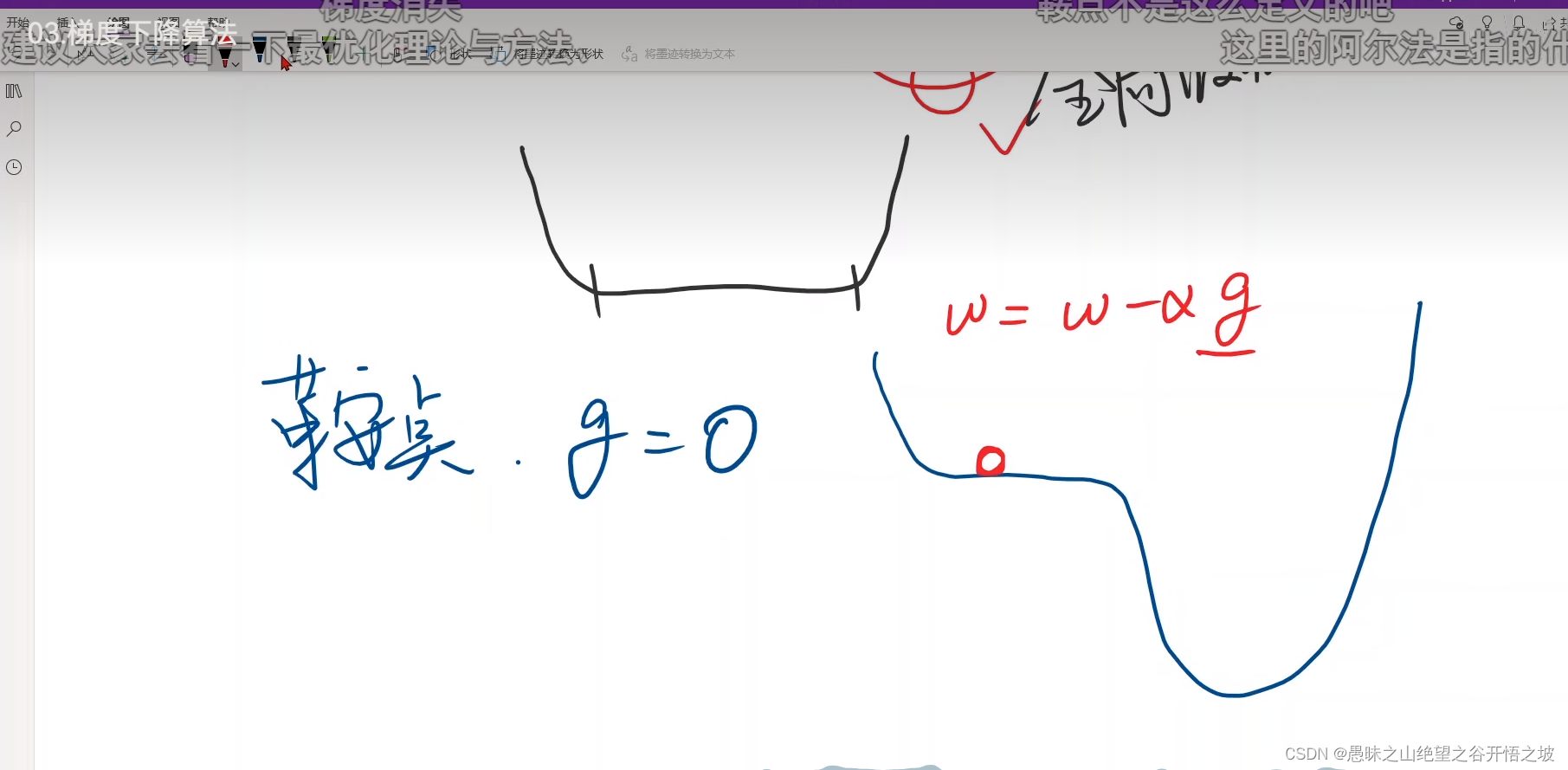
梯度的下降法,站在当前节点,梯度下降的方向,就是往最小值的方向
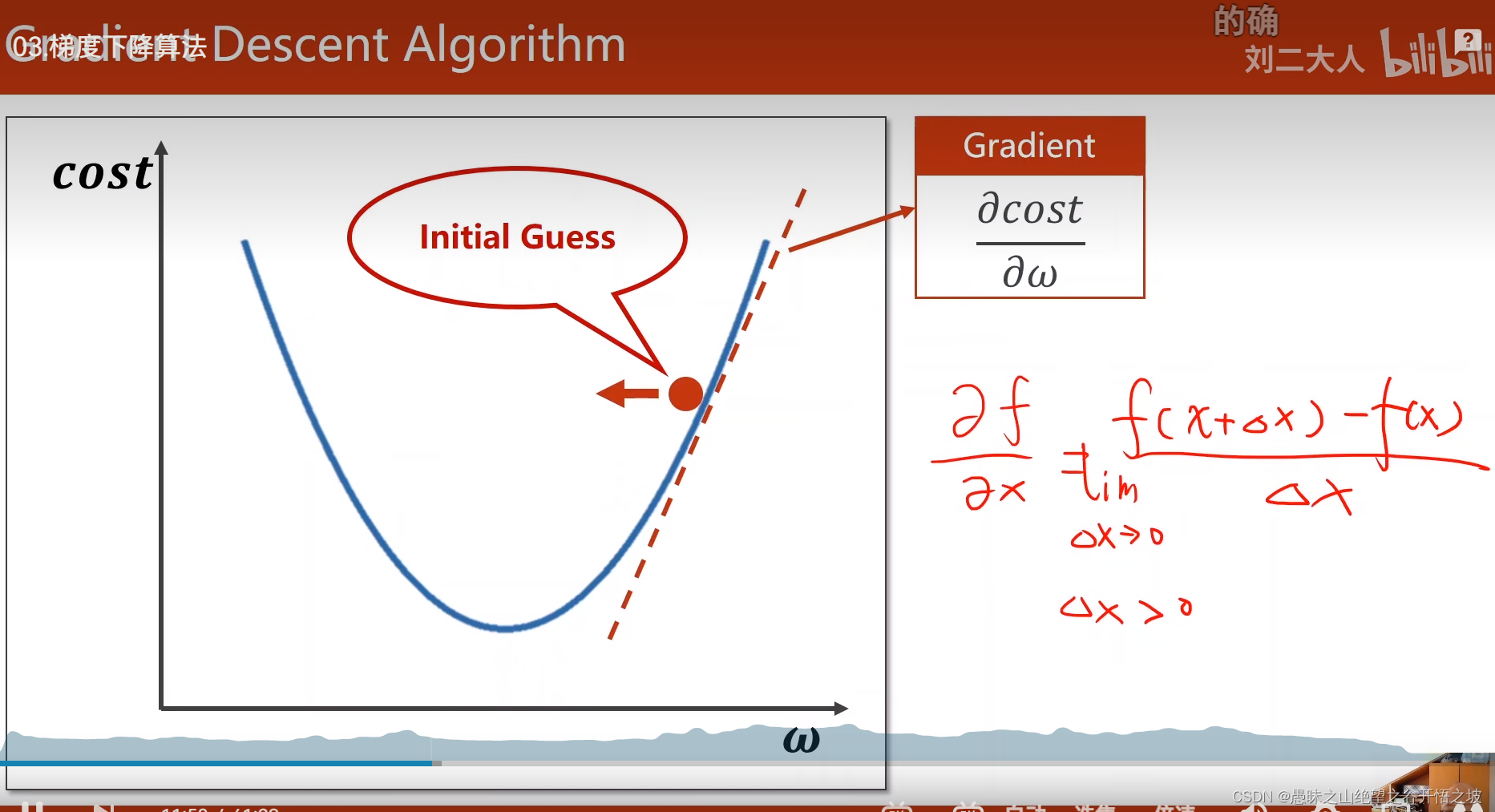
梯度就是导数,学习率不要过大,防止跳跃太大,对比人,人生道理都是一样
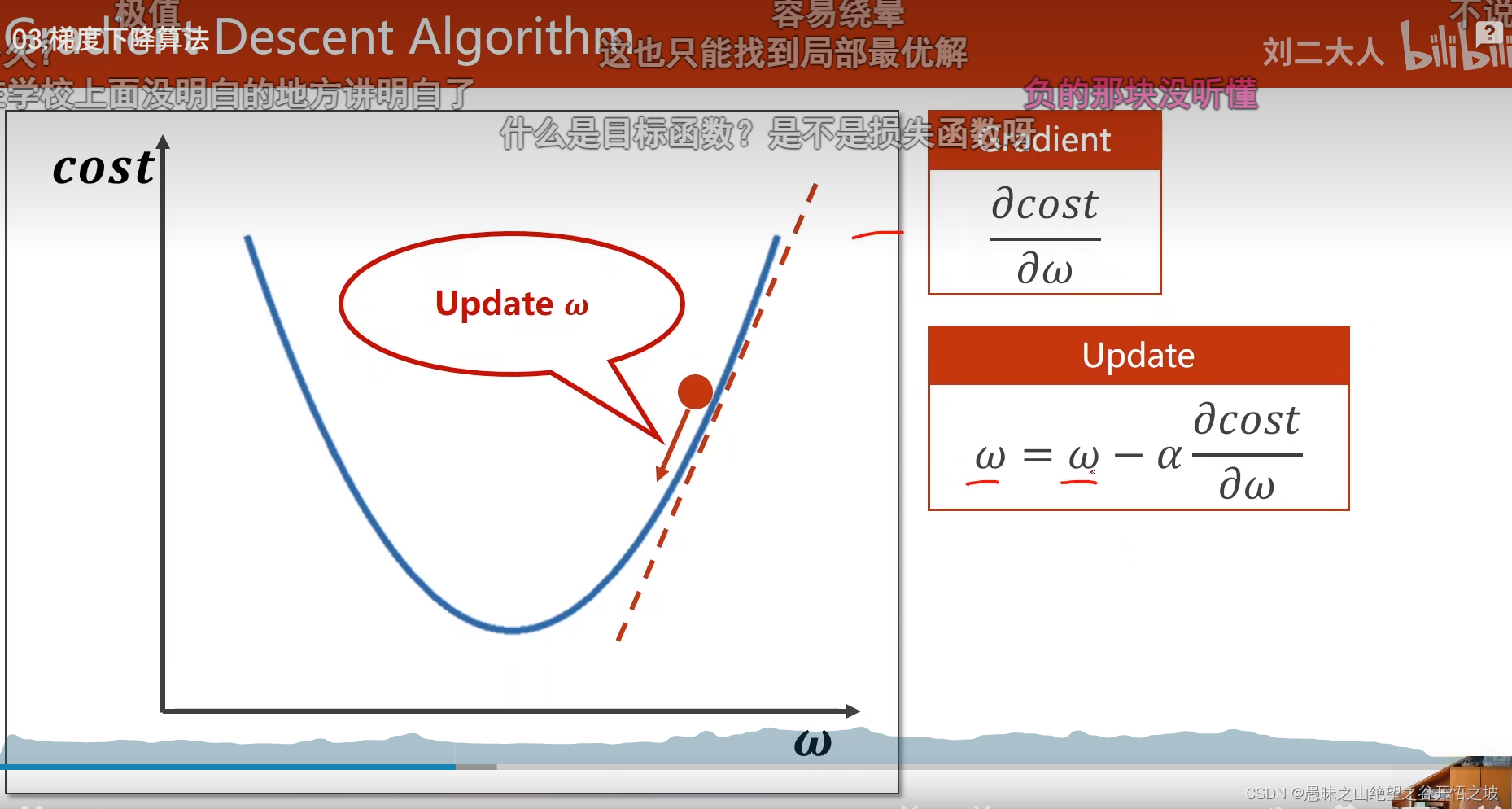
贪心思想,只看眼前最好的,也是只能得到局部最优,不一定得到全局最优

非凸函数
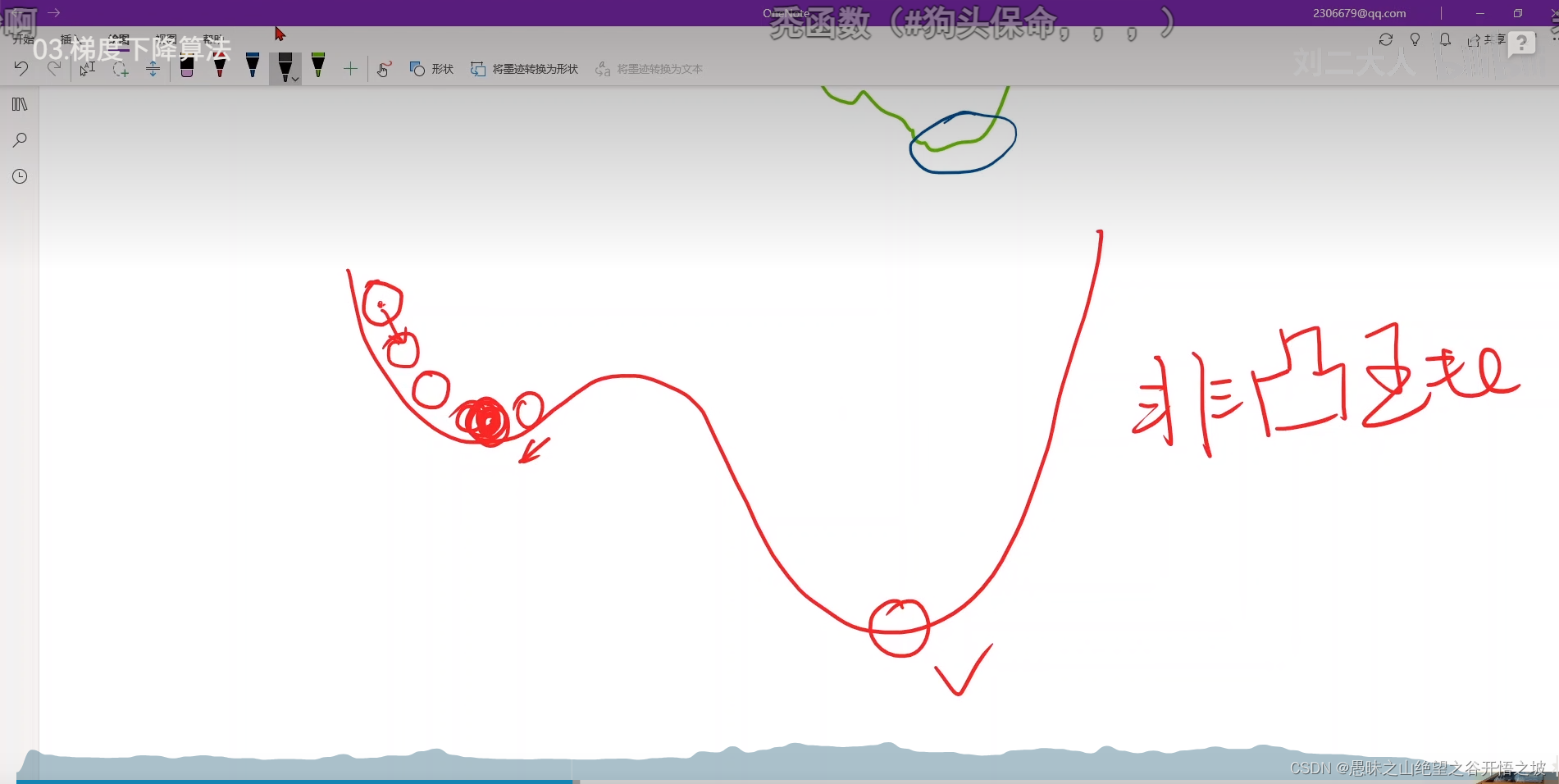
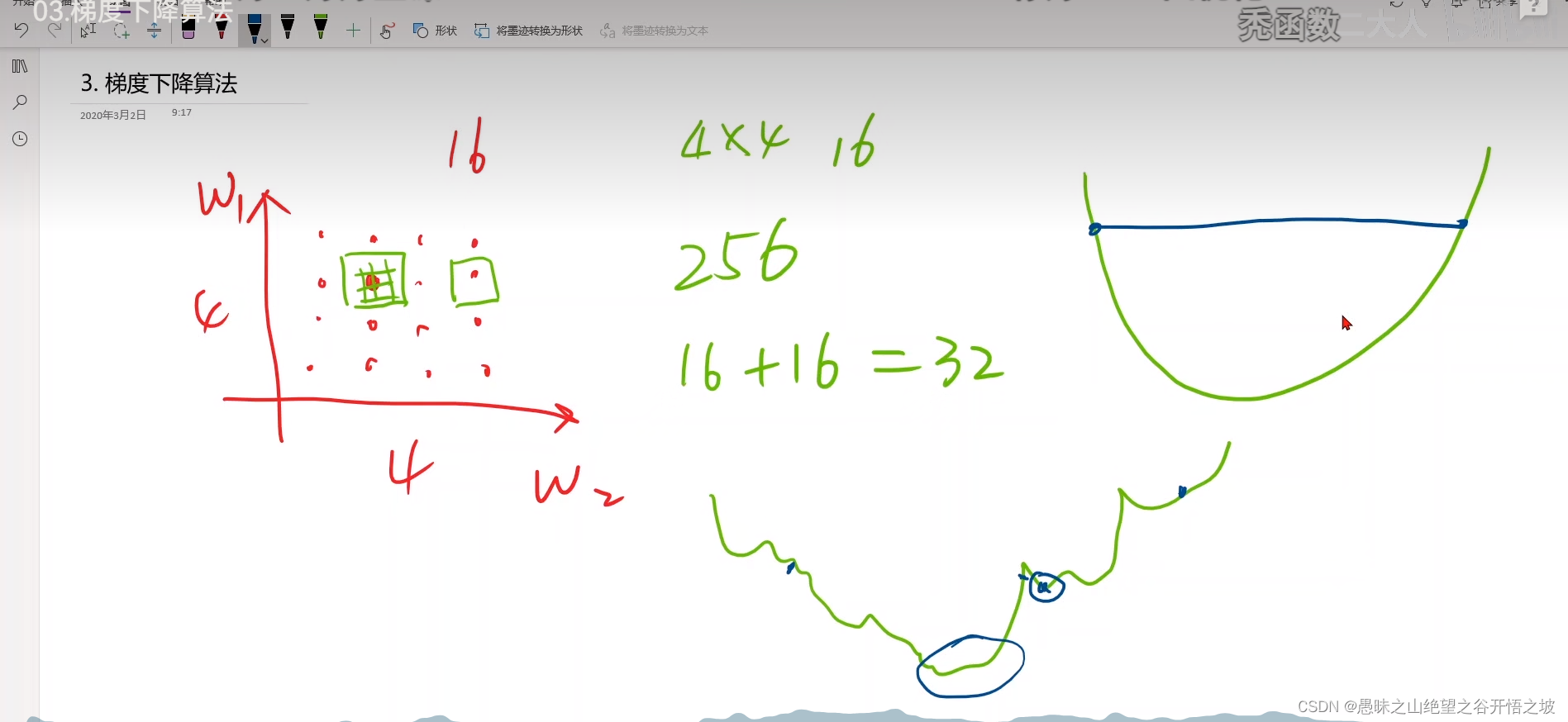
局部最优全局最优,深度学习一般没有多少局部最优点,实践证明
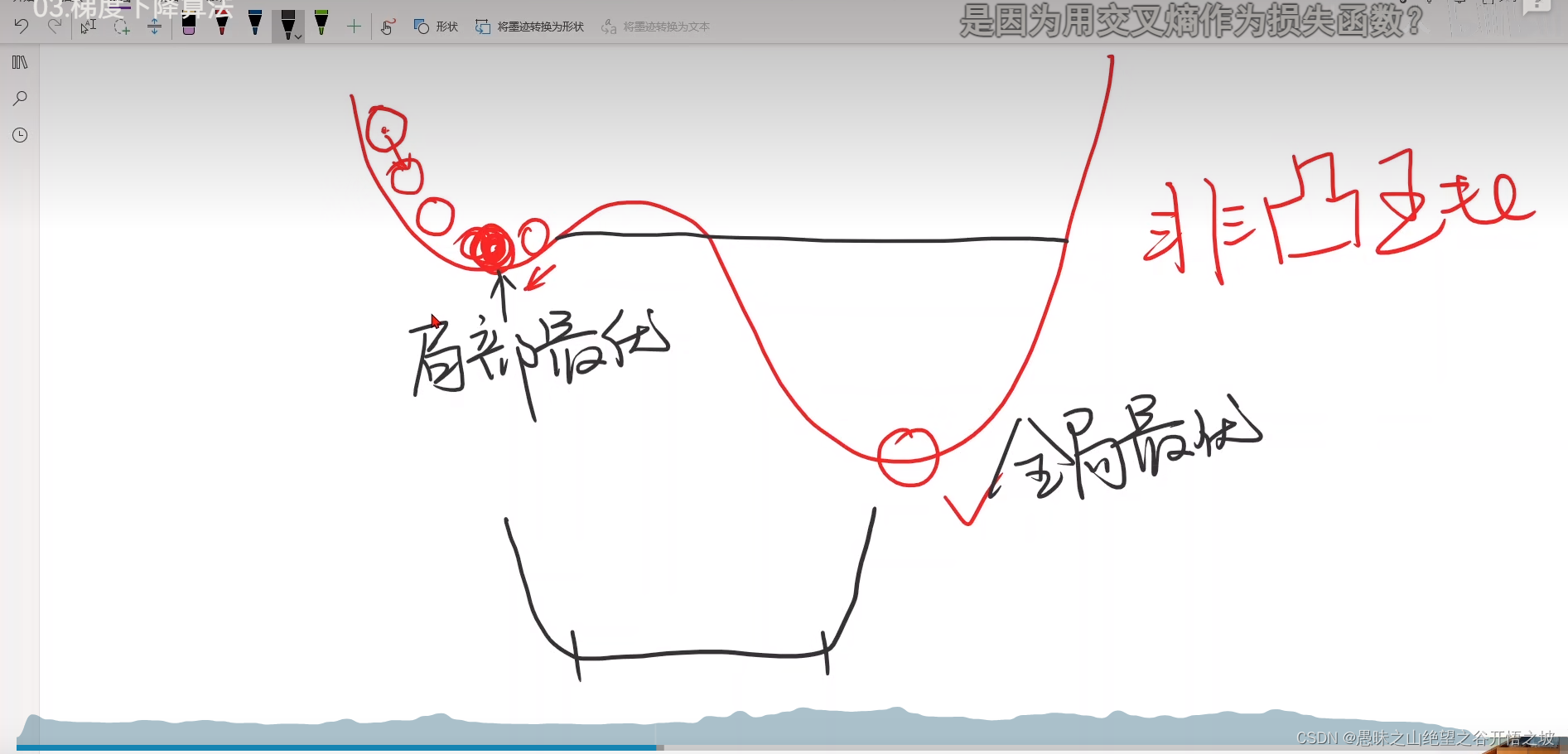
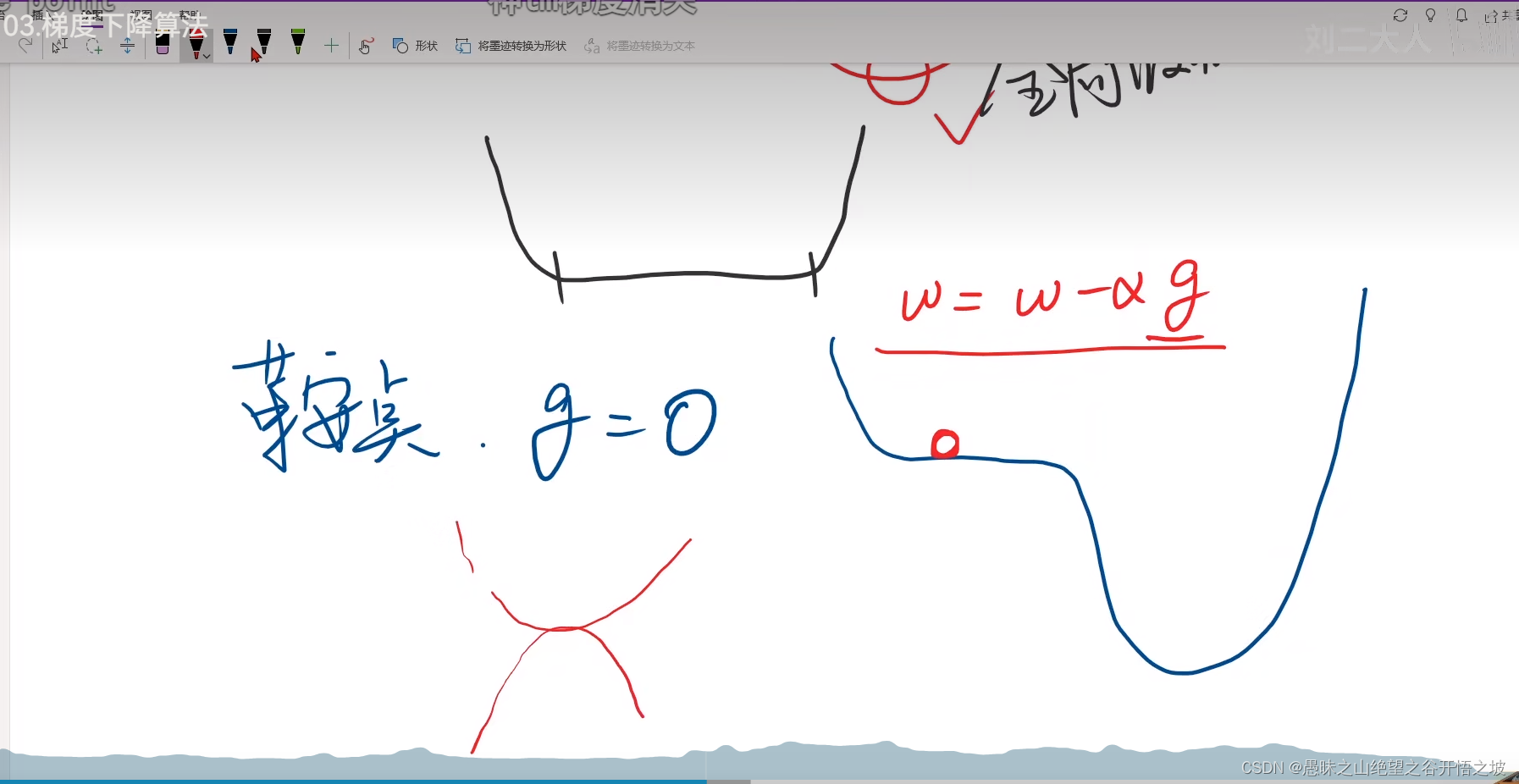
局部最小和局部最大的交接处,鞍点,梯度没法更新,走不动了,没法运动收敛了
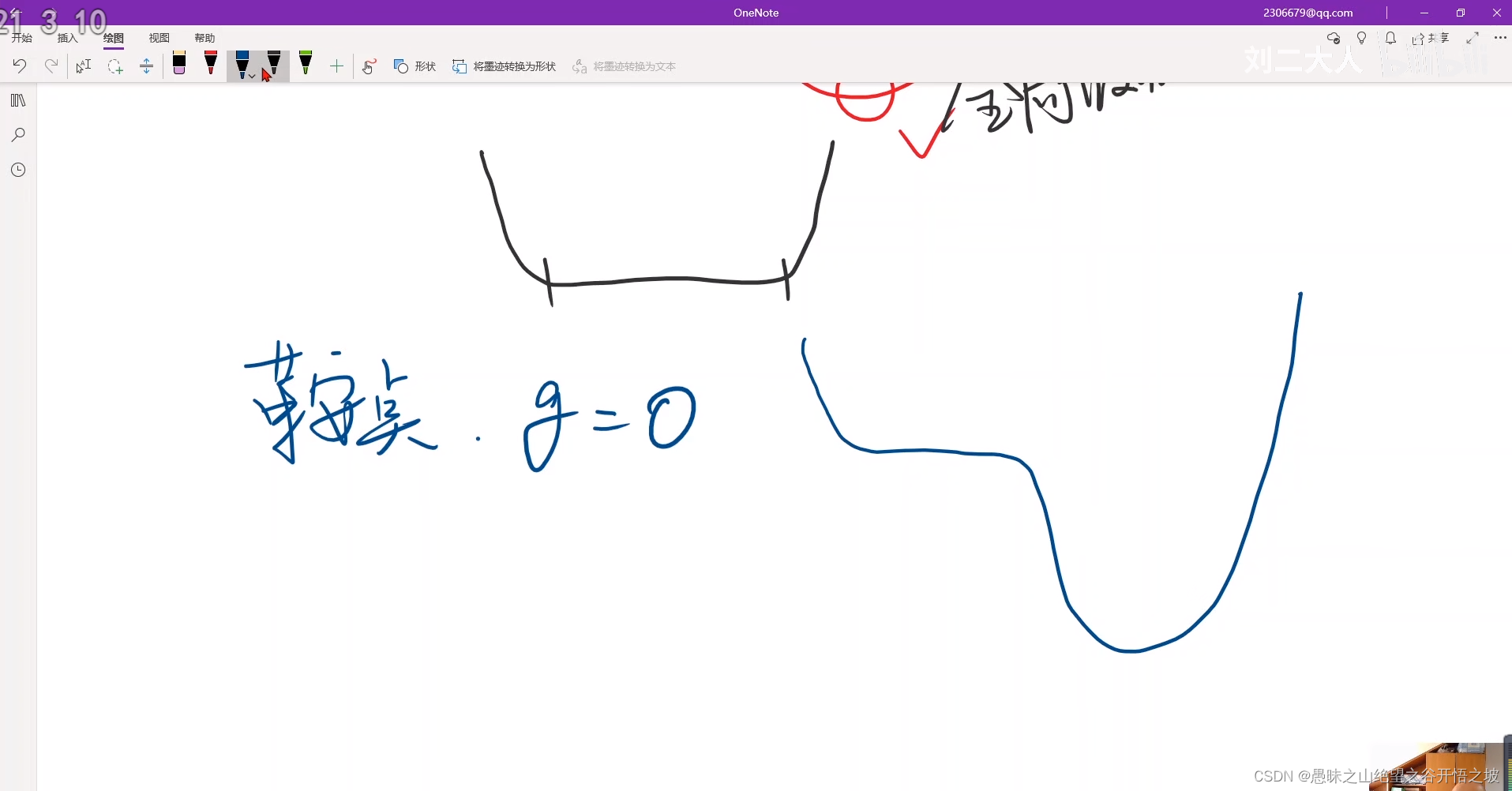
高维曲面的鞍点
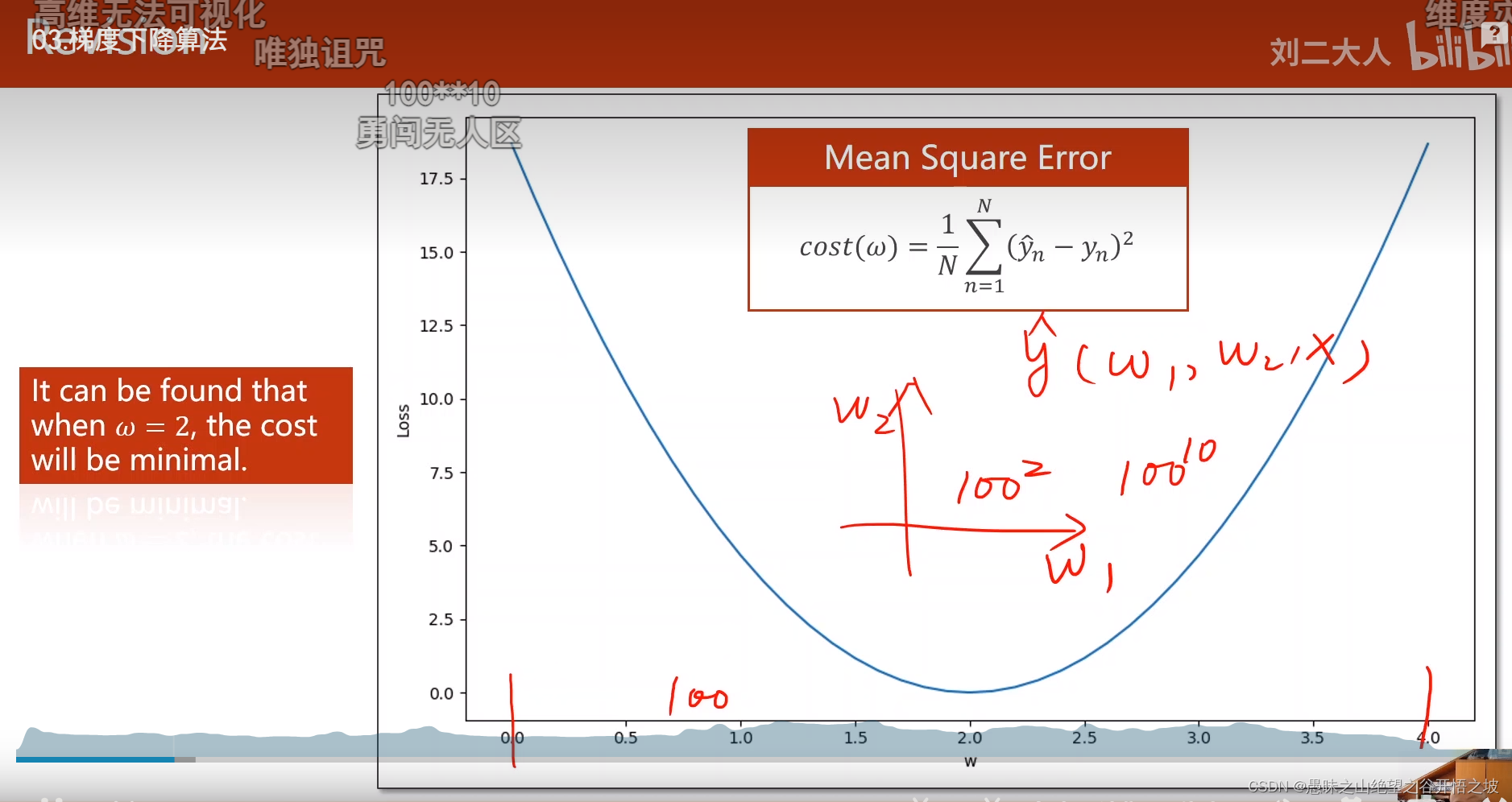
梯度计算公式

数据集
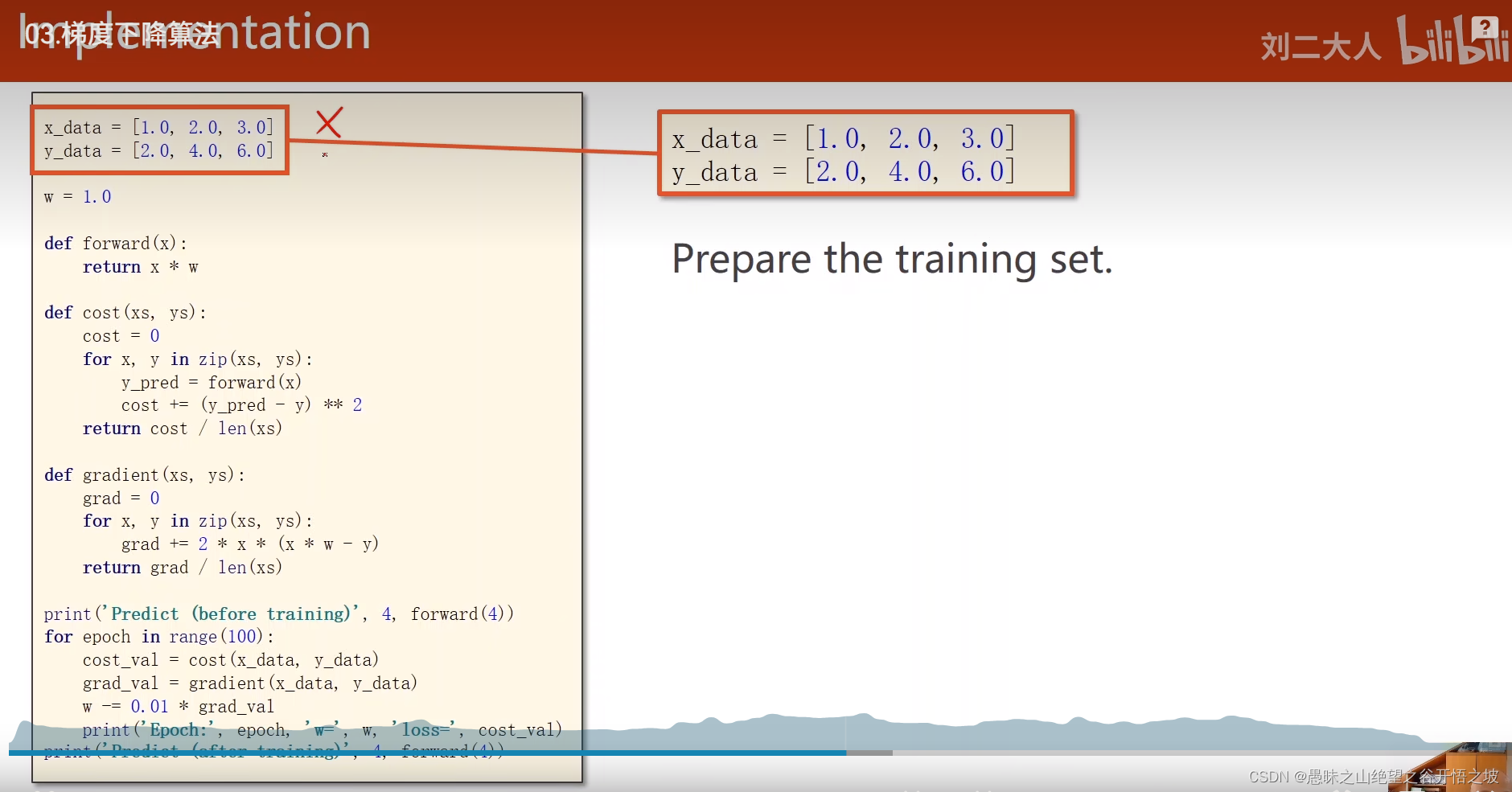
前馈计算
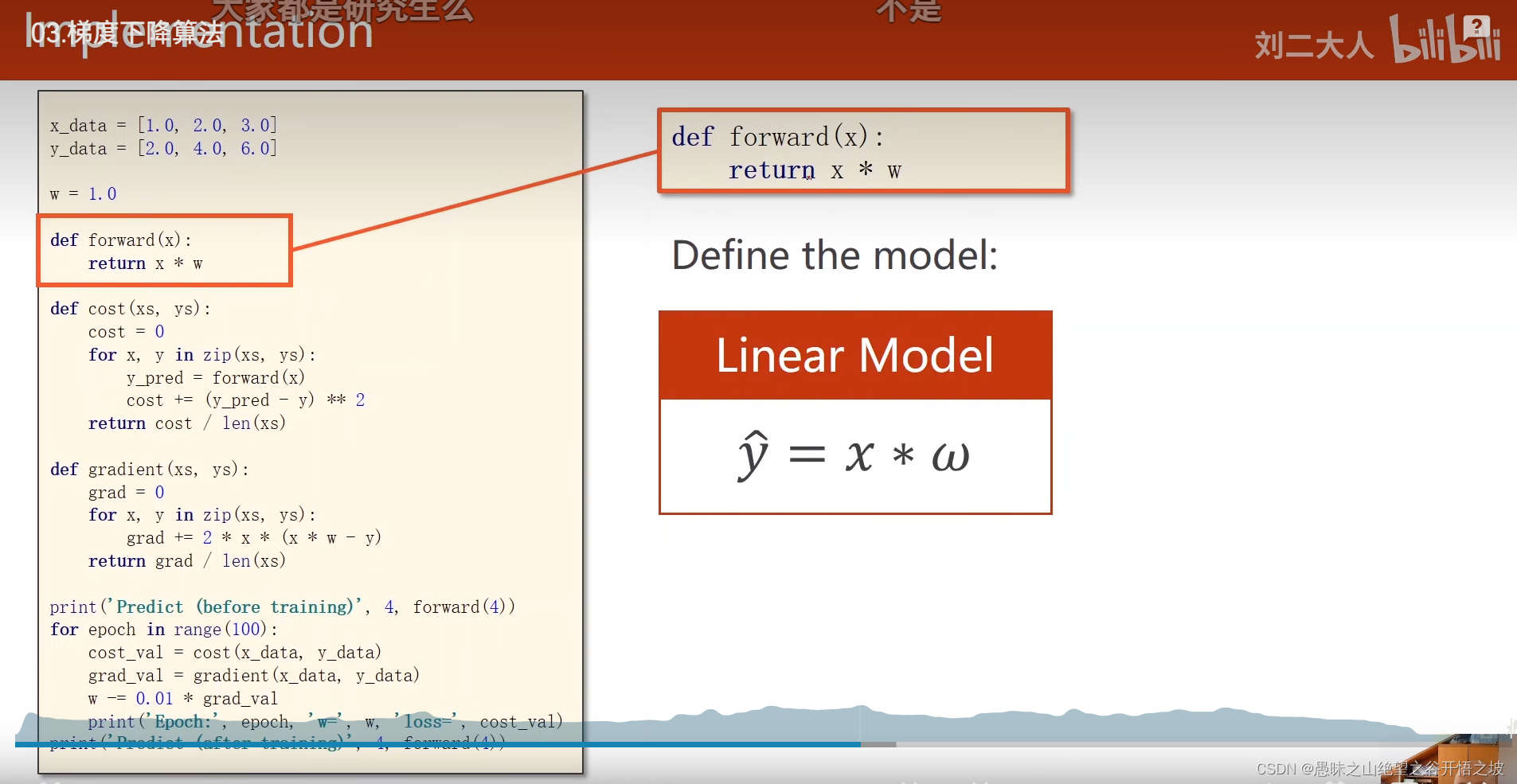
损失函数

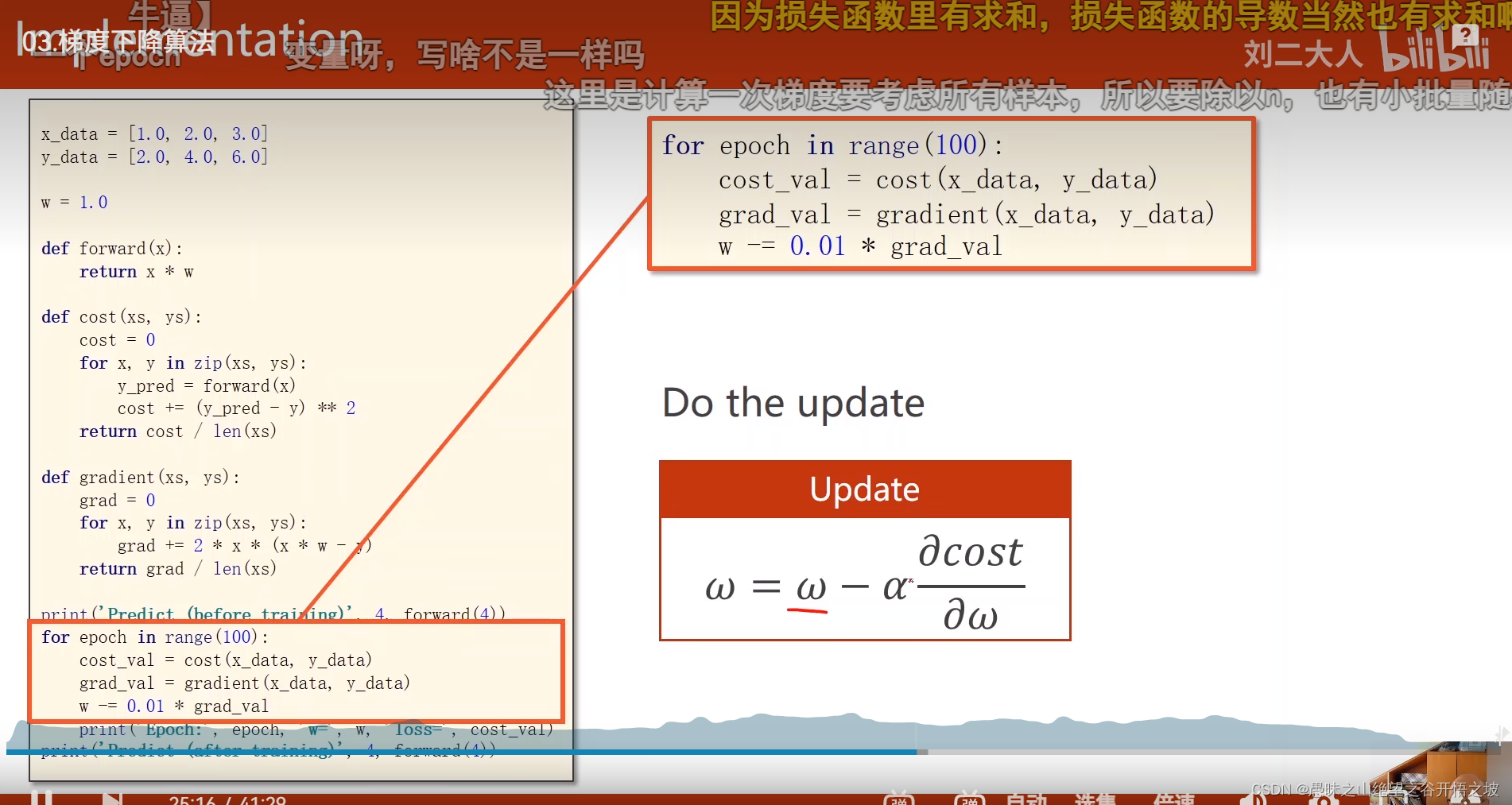
梯度求解

更新梯度
结果

指数加权均值,把cost弄成平滑,更容易观察整体下降趋势
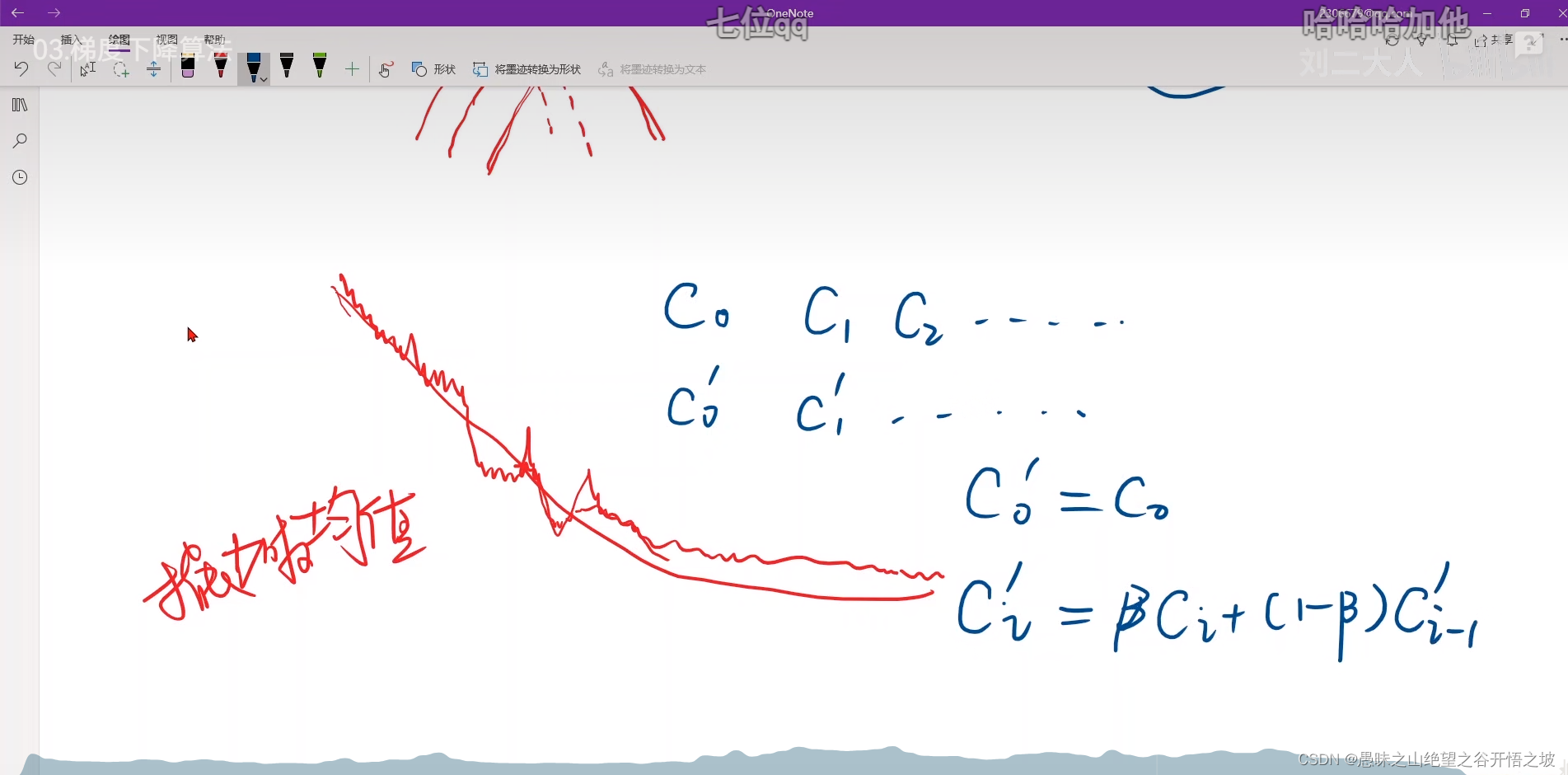
往往是学习率过大,没法收敛了,训练发散了
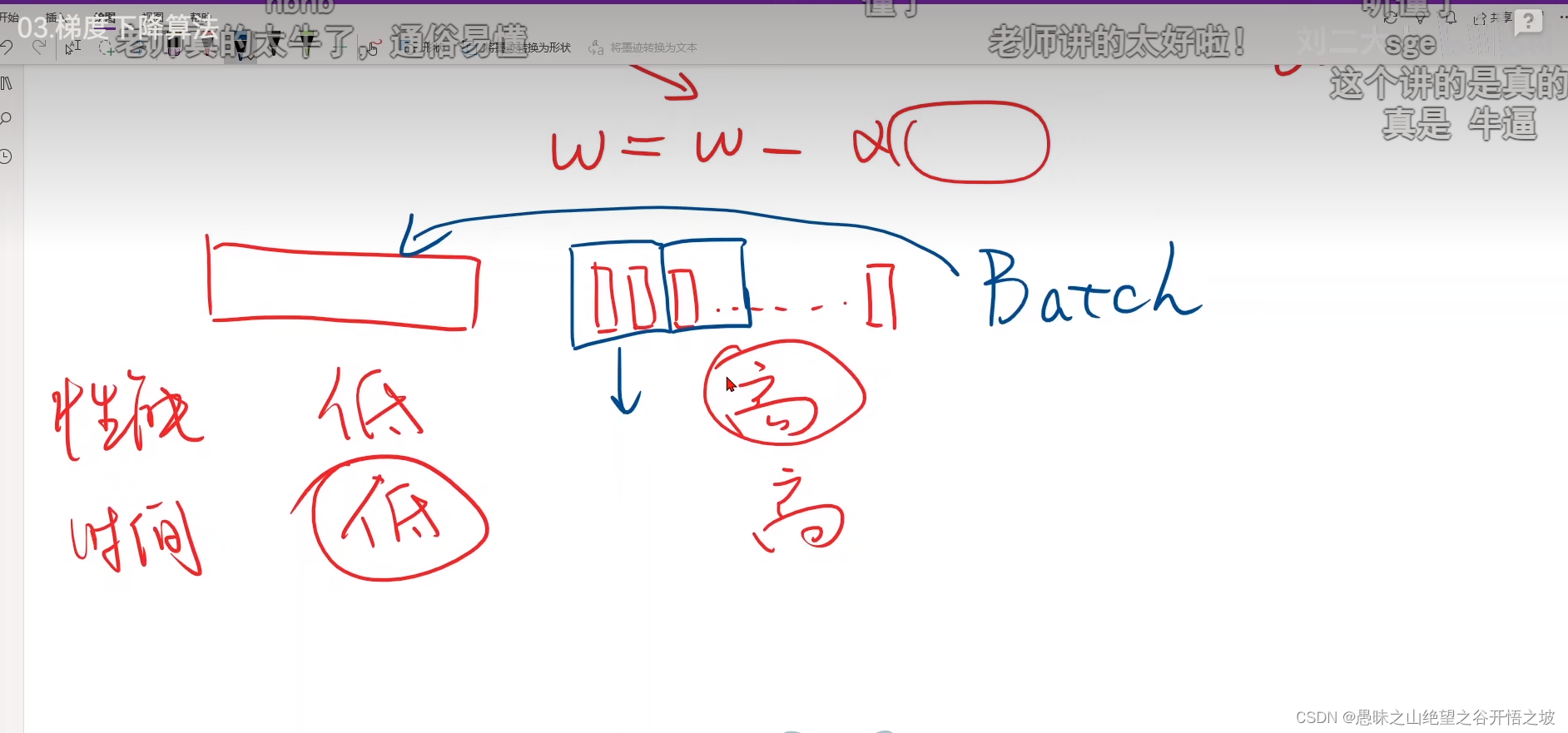
随机梯度下降,一个样本的损失就可以去更新参数了,而不是所有样本的平均损失,引入了随机性的噪声,遇到鞍点了也可能跨域,向前前进

随机梯度下降代码
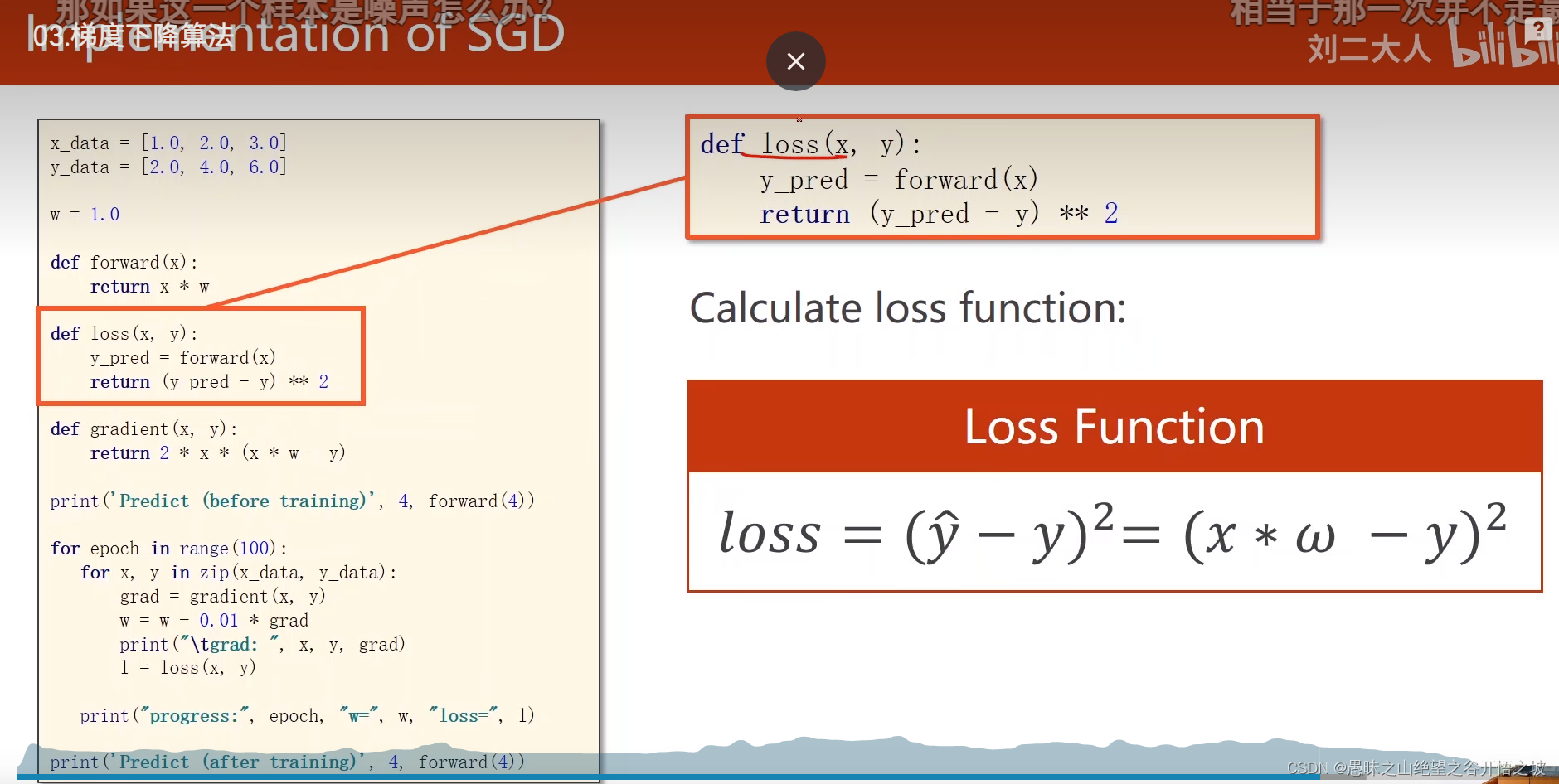
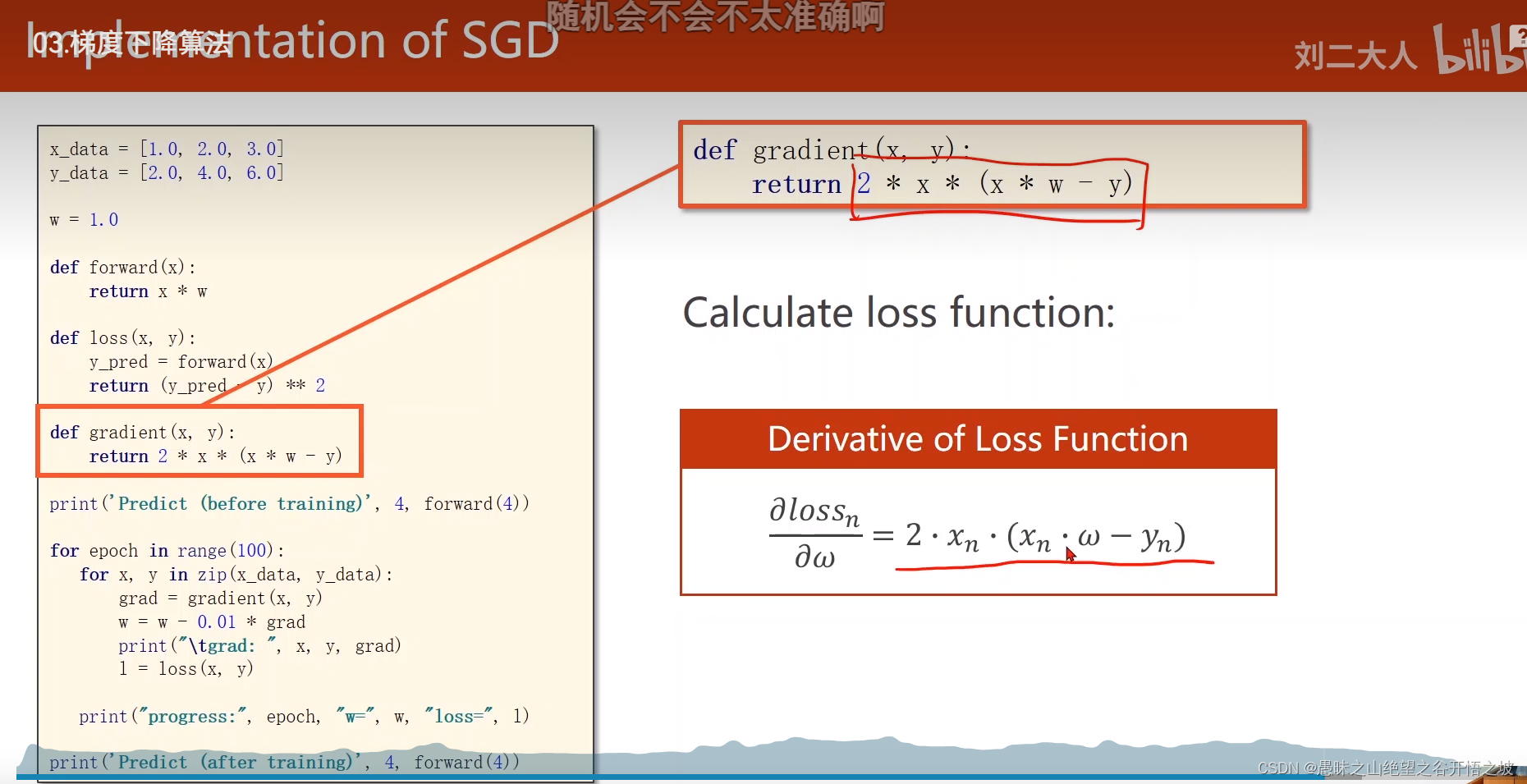
训练过程

梯度下降跨域并行计算,随机梯度没法并行,后一个样本依赖前面一个,时间复杂度过高
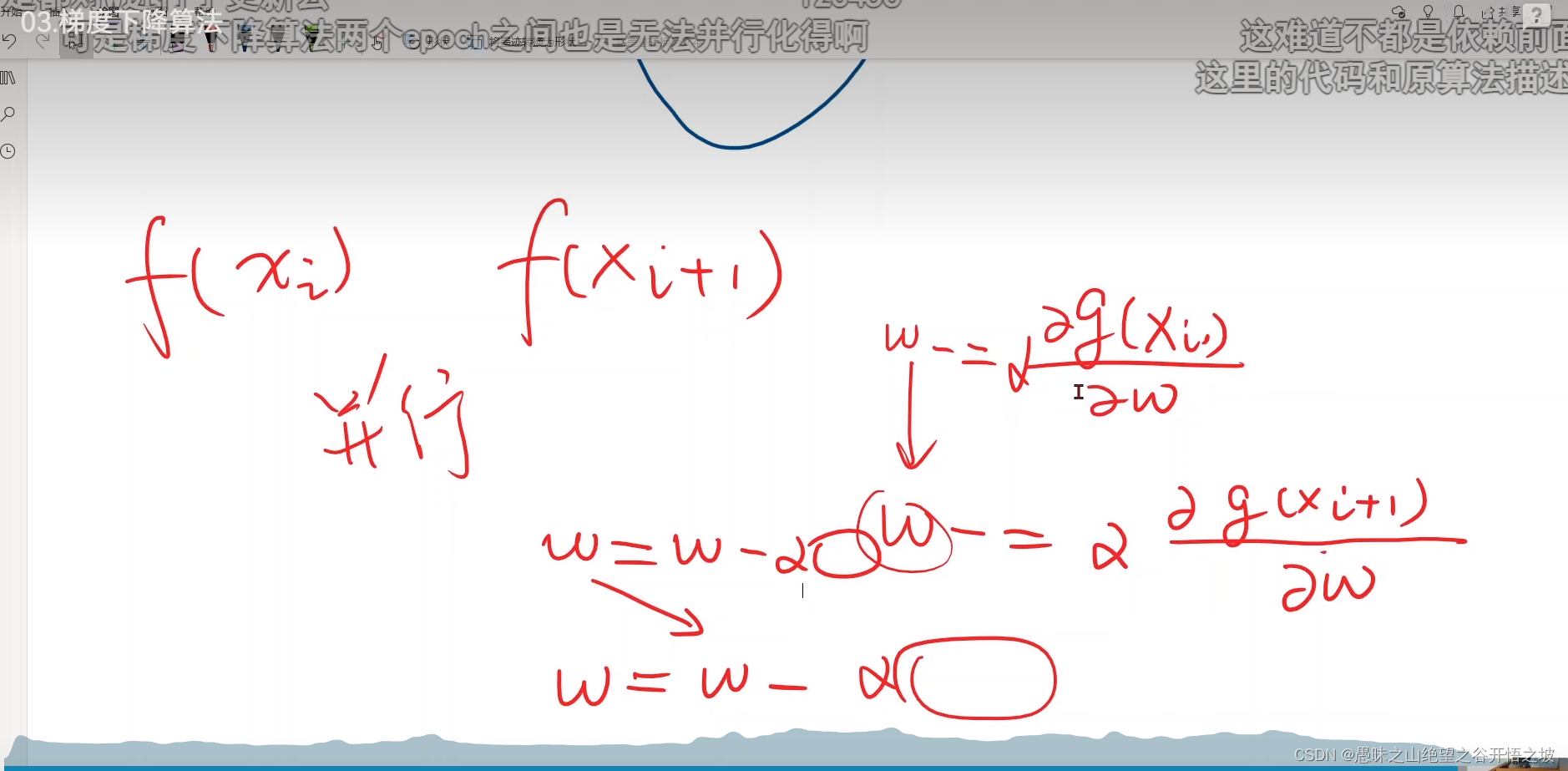
取个小批量的batch去训练,每次不是一个,也不是全部,而是小批量的,很有启发性,说到batch都是minibatch