目录
1.完全二叉树的节点个数
给你一棵 完全二叉树 的根节点 root ,求出该树的节点个数。
完全二叉树 的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层,则该层包含 1~ 2h 个节点。
题目来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/count-complete-tree-nodes

class Solution {
//1.遍历思路
int count = 0;
public int countNodes1(TreeNode root) {
if (root == null){
return 0;
}
count++;
countNodes(root.left);
countNodes(root.right);
return count;
}
//2子问题思路
public int countNodes(TreeNode root) {
if (root == null){
return 0;
}
return countNodes(root.left) + countNodes(root.right) + 1;
}
}2. 叶子节点个数
//1.遍历思路
int leafCount = 0;
int getLeafNodeCount1(TreeNode root) {
if (root == null) {
return 0;
}
if (root.left == null && root.right == null) {
leafCount++;
}
getLeafNodeCount(root.left);
getLeafNodeCount(root.right);
return leafCount;
}
//2.子问题思路
int getLeafNodeCount(TreeNode root) {
if (root == null) {
return 0;
}
if (root.left == null && root.right == null) {
return 1;
}
return getLeafNodeCount(root.left) + getLeafNodeCount(root.right);
}
3. 获取第K层节点的个数
/**
* 获取第K层节点的个数
* 子问题思路
*/
int GetKLeveNodeCount(TreeNode root, int k) {
if (root == null) {
return 0;
}
if (k == 1) {
return 1;
}
return GetKLeveNodeCount(root.left, k-1) + GetKLeveNodeCount(root.right, k-1);
}4. 二叉树的最大深度
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。

题目来源:力扣(LeetCode)
public int maxDepth(TreeNode root) {
if (root == null) {
return 0;
}
int leftDepth = maxDepth(root.left);
int rightDepth = maxDepth(root.right);
return leftDepth > rightDepth ? leftDepth+1 : rightDepth+1;
}5. 查找二叉树的value是否存在
TreeNode find(TreeNode root,char val) {
if (root == null) {
return null;
}
if (root.val == val) {
return root;
}
TreeNode ret = final (root.left, val);
if (ret != null) {
return ret;
}
ret = final (root.right, val);
if (ret != null) {
return ret;
}
return null;
}6. 是否是完全二叉树
boolean isCompleteTree(TreeNode root) {
if (root == null) {
return true;
}
Queue<TreeNode> queue = new LinkedList;
//进队列
queue.offer(root);
while (!queue.isEmpty()) {
TreeNode cur = queue.poll();
if (cur != null) {
queue.offer(left);
queue.offer(right);
}else {
break;
}
}
//出队列
while (!queue.isEmpty()) {
TreeNode top = queue.peek();
if (top != null) {
return false;
}
queue.poll();
}
return true;
}7. 相同的树
给你两棵二叉树的根节点 p 和 q ,编写一个函数来检验这两棵树是否相同。
如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
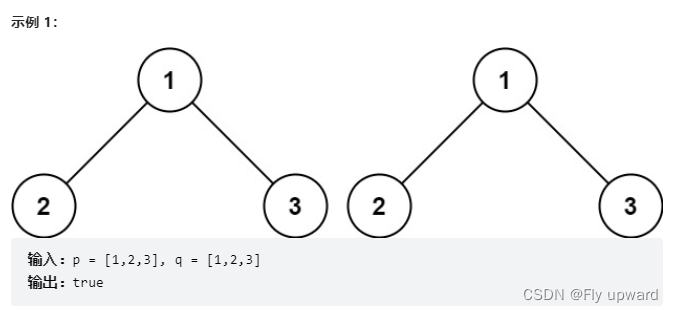
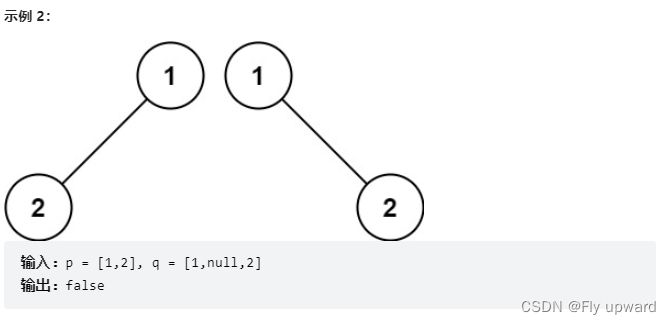
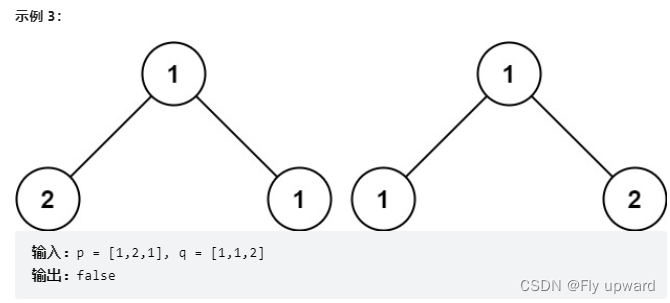
题目来源: 力扣(LeetCode)
public boolean isSameTree(TreeNode p, TreeNode q) {
if (p == null && q != null || p != null && q == null) {
return false;
}
if (p == null && q == null) {
return true;
}
if (q.val != p.val) {
return false;
}
return isSameTree(p.left,q.left) && isSameTree(p.right,q.right);
}8. 另一颗树的子树
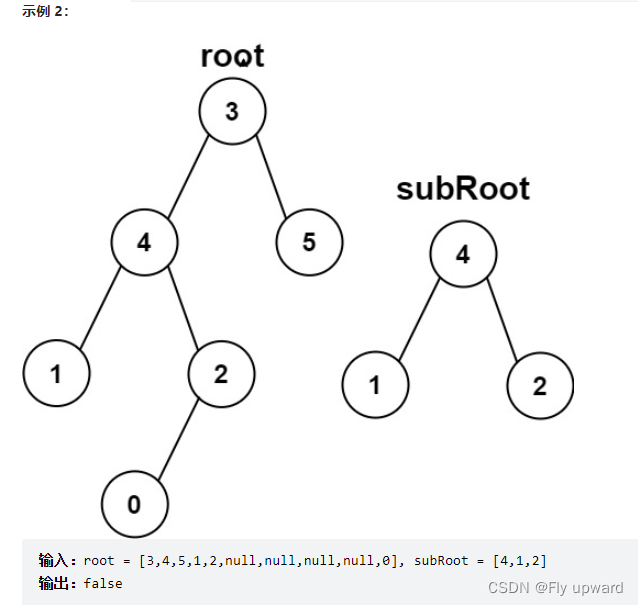
给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在,返回 true ;否则,返回 false 。
二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。
题目来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/subtree-of-another-tree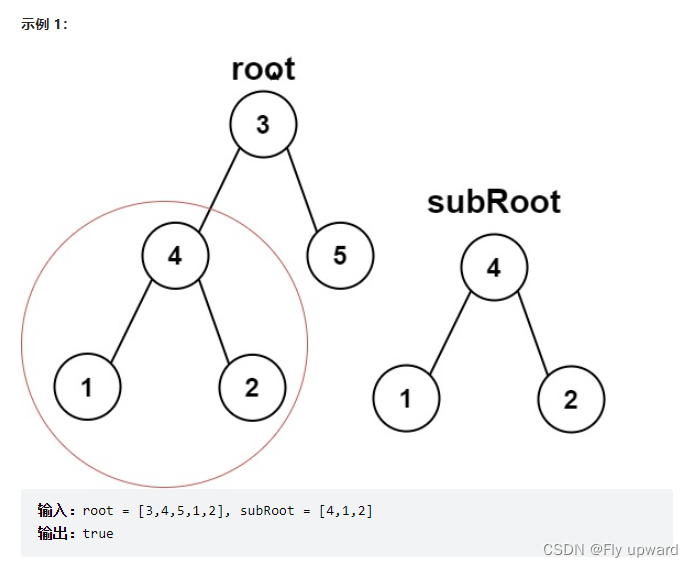
public boolean isSubtree(TreeNode root,TreeNode subRoot) {
if (root == null || subRoot == null) {
return false;
}
//根节点和subroot 是不是两颗相同的树
if (isSameTree(root,subRoot)) {
return true;
}
//subRoot 是不是root 的左子树
if (isSubtree(root.left,subRoot)) {
return true;
}
if (isSubtree(root.right,subRoot)) {
return true;
}
return false;
}9. 平衡二叉树
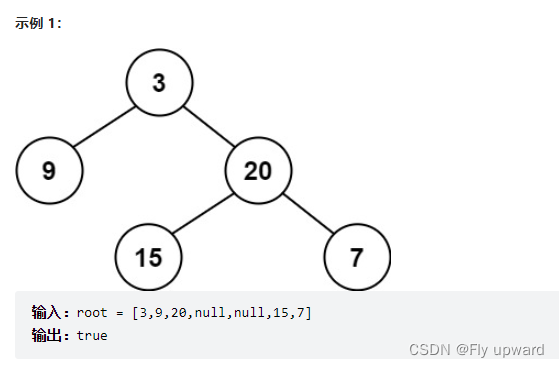
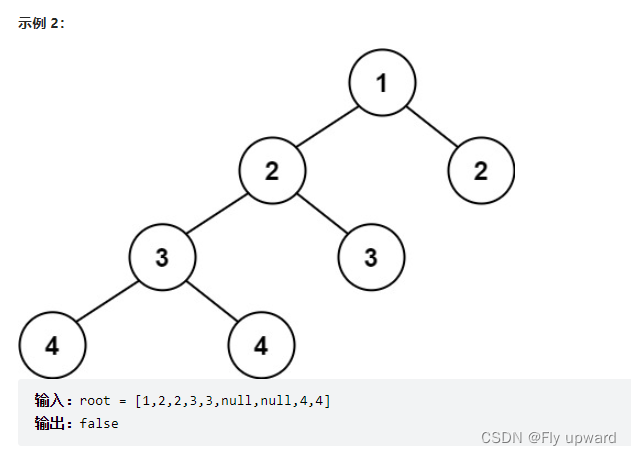
给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为:
一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1
题目来源:力扣(LeetCode)
解法一
//1.先查看深度
public int height(TreeNode root) {
if (root == null) {
return 0;
}
int leftHeight = height(root.left);
int rightHeight = height(root.right);
return (leftHeight > rightHeight) ? (leftHeight + 1) : (rightHeight + 1);
}
//2.查看左右子树深度差1则为平衡
public boolean isBalance(TreeNode root) {
if (root == null) {
return true;
}
int left = height(root.left);
int right = height(root.right);
return Math.abs(left - right) <= 1 && isBalanced(root.left) && isBalanced(root.right);
}
解法二
public int height(TreeNode root) {
if (root == null) {
return 0;
}
int leftHeight = height(root.left);
int rightHeight = height(root.right);
if (leftHeight >= 0 && rightHeight >= 0 && Math.abs(leftHeight-rightHeight) <= 1) {
return Math.max(leftHeight,rightHeight) + 1;
}else {
//说明不平衡
return -1;
}
}
public boolean isBalance(TreeNode root) {
if (root == null) {
return true;
}
return height(root) >= 0;
}
10. 对称二叉树
给你一个二叉树的根节点 root , 检查它是否轴对称。
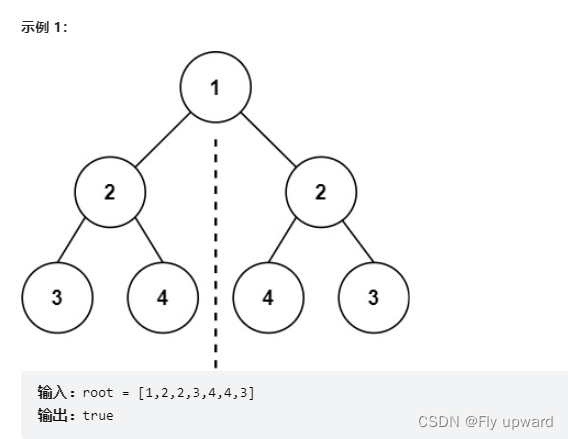
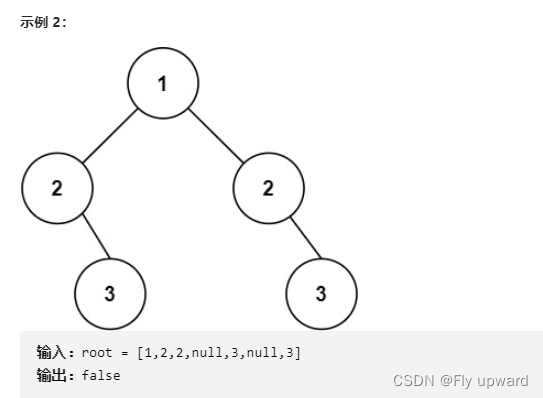
题目来源:力扣(LeetCode)
public boolean isSymmetricChild(TreeNode leftTree, TreeNode rightTree) {
if (leftTree == null && rightTree != null) return false;
if (leftTree != null && rightTree == null) return false;
if (leftTree == null && rightTree == null) return true;
if (leftTree.val != rightTree.val) return false;
return isSymmetricChild(leftTree.left,rightTree.right) &&
isSymmetricChild(leftTree.right,rightTree.left);
}
public boolean isSymmetric(TreeNode root) {
if (root == null) {
return true;
}
return isSymmetricChild(root.left ,root.right);
}
11. 二叉树的层序遍历
给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)
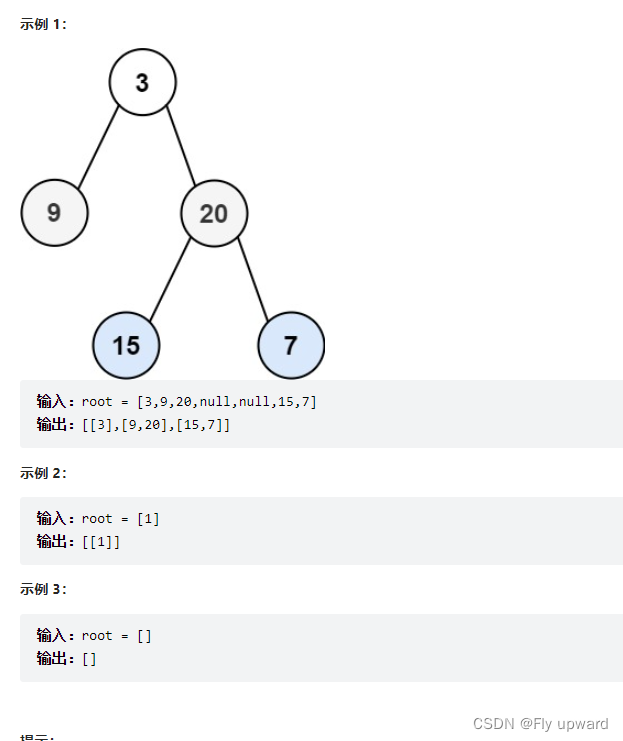
题目来源:力扣(LeetCode)
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> ret = new ArrayList<>();
if (root == null) return ret;
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty) {
int size = queue.size();//当前层有多少个节点
List<Integer> lst = new ArrayList<>();
while (size != 0) {
TreeNode cur = queue.poll();
list.add(cur.val);
if (cur.left != null) {
queue.offer(cur.left);
}
if (cur.right != null) {
queue.offer(cur.right);
}
size--;
}
ret.add(list);
}
return ret;
}
12. 二叉搜索树的最近公共祖先
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。
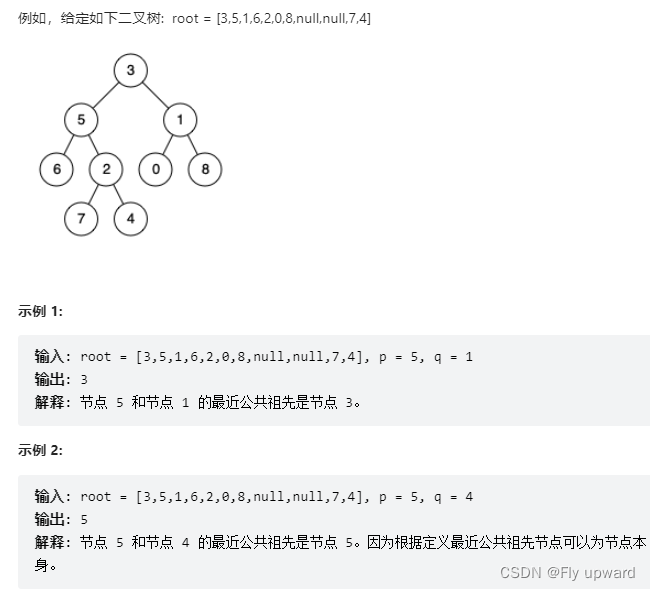
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/er-cha-shu-de-zui-jin-gong-gong-zu-xian-lcof
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if (`root == null) {
return null;
}
if (root == p || root == q) {
return root;
}
TreeNode leftT = lowestCommonAncestor(root.left,p,q);
TreeNode rightT = lowestCommonAncestor(root.right,p,q);
if (leftT != null && rightT != null) {
return root;
}else if (leftT != null) {
return leftT;
}else {
return rightT;
}
}13. 二叉搜索树 转换为排序的双向链表
TreeNode prev = null;
public void inorder(TreeNode pCur) {
if (pCur == null) {
return;
}
inorder(pCur.left);
pCur.left = prev;
if (prev != null) {
prev.right = pCur;
}
prev = pCur;
inorder(pCur.right);
}
public TreeNode Convert(TreeNode pRootOfTree) {
if (pRootOfTree == null) {
return null;
}
inorder(pRootOfTree);
TreeNode head = pRootOfTree;
while (head.left != null) {
head = head.left;
}
return head;
}