文章目录
第一题: 205. 同构字符串
LeetCode: 205. 同构字符串
描述:
给定两个字符串 s 和 t ,判断它们是否是同构的。
如果 s 中的字符可以按某种映射关系替换得到 t ,那么这两个字符串是同构的。
每个出现的字符都应当映射到另一个字符,同时不改变字符的顺序。不同字符不能映射到同一个字符上,相同字符只能映射到同一个字符上,字符可以映射到自己本身。

解题思路:
- 哈希表解题
- 遍历两个字符串, 遍历到的s的字符为
ch1, 遍历到的t的字符为ch2- 哈希表1记录 (ch1,ch2) 哈希表2 记录 (ch2,ch1)
- 如果当前哈希表1存在ch1, 查看哈希表中对应的值是否等于ch2
- 如果当前哈希表2存在ch2, 查看哈希表中对应的值是否等于ch1
代码实现:
class Solution {
public boolean isIsomorphic(String s, String t) {
Map<Character,Character> map1 = new HashMap<>();
Map<Character,Character> map2 = new HashMap<>();
for(int i = 0; i < s.length(); i++) {
char ch1 = s.charAt(i);
char ch2 = t.charAt(i);
if((map1.containsKey(ch1)&&map1.get(ch1)!=ch2)||(map2.containsKey(ch2)&&map2.get(ch2)!=ch1)){
return false;
}
map1.put(ch1,ch2);
map2.put(ch2,ch1);
}
return true;
}
}
第二题: 216. 组合总和 III
LeetCode: 216. 组合总和 III
描述:
找出所有相加之和为 n 的 k 个数的组合,且满足下列条件:
- 只使用数字1到9
- 每个数字 最多使用一次
返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次,组合可以以任何顺序返回。


解题思路:
- 这里使用回溯解法
- 注意这里的剪枝
- 剪枝: 不能使用重复的元素
- 剪枝: 如果当前的 数字 大于 n, 就不能继续使用了
- 如果当前list大小等于k, 且 n==0. 就加入结果集中
代码实现:
class Solution {
List<List<Integer>> res = new ArrayList<>();
List<Integer> list = new ArrayList<>();
public List<List<Integer>> combinationSum3(int k, int n) {
bfs(k,n,1);
return res;
}
public void bfs(int k, int n, int index) {
if(list.size() == k && n == 0){
res.add(new ArrayList<>(list));
return;
}
for(int i = index; i <= 9; i++) {
if(i > n){
break;
}
n -= i;
list.add(i);
bfs(k,n,i+1);
n +=i;
list.remove(list.size()-1);
}
}
}
第三题: 377. 组合总和 Ⅳ
LeetCode: 377. 组合总和 Ⅳ
描述:
给你一个由 不同 整数组成的数组 nums ,和一个目标整数 target 。请你从 nums 中找出并返回总和为 target 的元素组合的个数。
题目数据保证答案符合 32 位整数范围。

解题思路:
- 注意这题如果使用回溯的话, 会超时
- 这里使用动态规划解题.
- 状态 F(i) : 组合为i时,使用nums中的数能够组成组合的个数
- 状态转移方程: i >= num dp[i] += dp[i-num]
- 初始化: F(0) = 1;
- 返回结果: F(target)
代码实现:
class Solution {
public int combinationSum4(int[] nums, int target) {
int[] dp = new int[target+1];
dp[0] = 1;
for(int i = 1; i <= target; i++) {
for(int num : nums) {
if(i >= num) {
dp[i] += dp[i-num];
}
}
}
return dp[target];
}
}
第四题: 257. 二叉树的所有路径
LeetCode: 257. 二叉树的所有路径
描述:
给你一个二叉树的根节点 root ,按 任意顺序 ,返回所有从根节点到叶子节点的路径。
叶子节点 是指没有子节点的节点
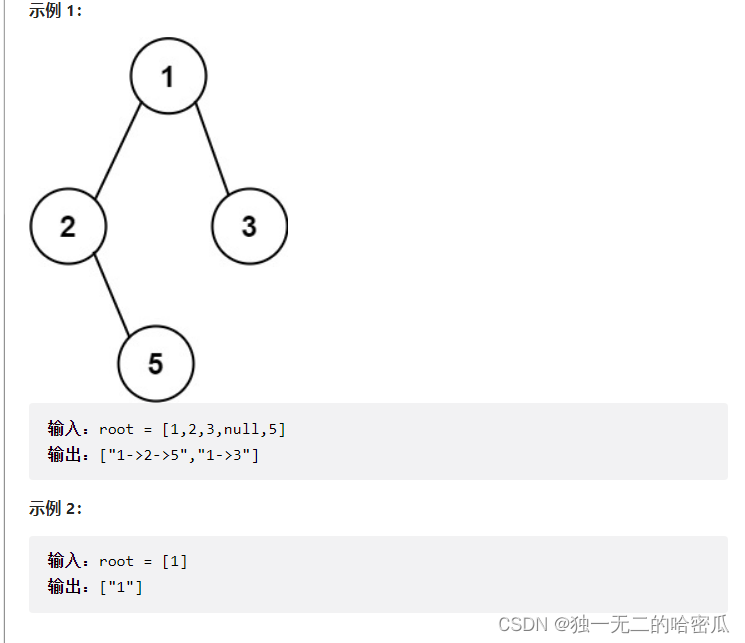

解题思路:
- 这里使用回溯解题
- 从根节点一直往叶子节点走, 进行节点值的拼接
- 如果当前为叶子节点, 就把拼接好的字符串添加到结果集中
代码实现:
class Solution {
List<String> res = new ArrayList<>();
public List<String> binaryTreePaths(TreeNode root) {
StringBuilder sb = new StringBuilder();
dfs(root,"");
return res;
}
public void dfs(TreeNode root, String sb) {
if(root==null) return;
sb += root.val;
if(root.left == null && root.right == null) {
res.add(sb);
return;
}
dfs(root.left,sb+"->");
dfs(root.right,sb+"->");
}
}
第五题: 313. 超级丑数
LeetCode: 313. 超级丑数
描述:
超级丑数 是一个正整数,并满足其所有质因数都出现在质数数组 primes 中。
给你一个整数 n 和一个整数数组 primes ,返回第 n 个 超级丑数 。
题目数据保证第 n 个 超级丑数 在 32-bit 带符号整数范围内。

解题思路:
- 相当于提供一个 primes = [2,3,5]
- 就有三个数列
- 2, 4, 6, 8 … 2*n
- 3, 6, 9, 12, … 3 *n
- 5, 10, 15, 20, … 5*n
- 依次添加最小的, 注意去重
- 这里使用优先级队列来完成
- 将所有数列都添加到堆中
- 依次出堆顶元素 n 次
- 注意去重的情况, 如果当前堆不为空, 且有重复, 就一直出堆顶元素,
代码实现:
class Solution {
public int nthSuperUglyNumber(int n, int[] primes) {
PriorityQueue<Long> queue = new PriorityQueue<>();
long res = 1;
for(int i = 1; i < n; i++) {
for(int prime : primes) {
queue.add(prime*res);
}
res = queue.poll();
while(!queue.isEmpty() && res == queue.peek()) {
queue.poll();
}
}
return (int) res;
}
}
第六题: 343. 整数拆分
LeetCode: 343. 整数拆分
描述:
给定一个正整数 n ,将其拆分为 k 个 正整数 的和( k >= 2 ),并使这些整数的乘积最大化。
返回 你可以获得的最大乘积 。

解题思路:
- 如果当前n是小于4的情况, 拆分的情况是固定的, 2 只能拆成11最大为1, 3只能拆成21最大为2, 4只能拆成最大2*2为4.
- 大于4的情况, 每次拆分都多拆成3, 尽可能的多拆3出来.
代码实现:
class Solution {
public int integerBreak(int n) {
if(n == 2) return 1;
if(n == 3) return 2;
int res = 1;
while(n > 4) {
n -= 3;
res *= 3;
}
return res * n;
}
}